I think we can assemble a chain of reasoning now that makes the pentagon-decagon-hexagon identity seem close to inevitable!
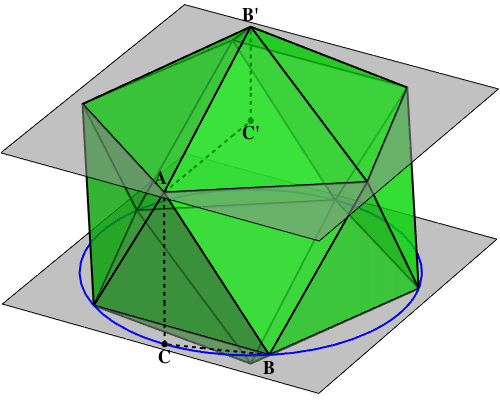
Suppose we take three congruent rectangles, and assemble them symmetrically so that their long edges are all mutually orthogonal, and their short edges are all mutually orthogonal. Like this:
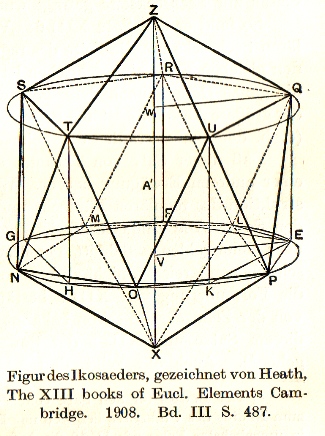
We then join up the corners to make an icosahedron, as in the diagram above. Eight faces of this icosahedron (the ones centred on the diagonals of the eight “octants” into which the space here is divided) will always be congruent and equilateral; that’s guaranteed by the construction, whatever the precise ratio of the side lengths of the rectangles. The other twelve faces will be isosceles triangles, all congruent to each other.
Now, it’s clear that by making the rectangles long and skinny, we can make the isosceles triangles as long and skinny as we like. But what about making them short and squat? How far can we go in that direction?
If we make the three rectangles into squares, as above, the isosceles triangles have two 45° angles. So between this extreme, and the long-and-skinny extreme, it’s clear that we can choose some intermediate degree of skinniness for the rectangles that will turn the 12 isosceles triangles into equilateral triangles.
So, a regular icosahedron must exist, and it will have six edges that form three mutually orthogonal pairs.
Having reached that conclusion, we can now use the construction below, where we project everything into the plane of one of our rectangles.
1
Φ
Φ
1
A
B
′
–A
–B
′
C
′
P
Q
R
S
O
T
α
α
α
90–α
We can’t yet justify the specific value, , that we’ve written here as the length of the rectangles … but we don’t need to!
Without any calculations that depend on , we can see that is parallel to , and that both are orthogonal to . That’s enough to show that the triangle is congruent to triangle , and hence the distance between the pentagons, , equals their radius, .
Now we can appeal to John’s original construction:

is a pentagon edge, is a decagon edge, and is the radius of the circle in which the pentagon and decagon are inscribed. So the congruent right triangles and constitute proofs of the pentagon-decagon-hexagon identity.
And then, as a final bonus, we can simply appeal to Euclid’s golden triangle lemma – which gives us the ratio between the radius and the decagon edge length as – and work backwards to show that this is also the ratio of length to width for our three orthogonal rectangles.
This follows simply from the fact that the right triangle is similar to the right triangle .








Re: This Week’s Finds in Mathematical Physics (Week 283)
There are a couple of nice pictures at the bottom of the webpage. Notice the Faces and Points alternating symmetry.
Phi and Geometry.
Solid …………….Dodecahedron…………Icosahedron
Face shape ………..Pentagon………………Triangle
Faces ………………..12 ……………………..20
Points ………………..20 ……………………..12
Edges ………………..30 ……………………..30