The Weaire–Phelan Structure
Posted by John Baez
“Oh no!” you think, reading the title of this post. “Yet another obscure mathematical structure! I’m still struggling with Polish spaces, Hilsum–Skandalis maps, and Fell bundles. Sometimes I wish those bloggers at the -Café would just shut up and let me think.”
You’ll be relieved, perhaps, that the Weaire–Phelan structure is something you can actually see. In fact, it was chosen as the design for the National Aquatics Center for the 2008 Olympics — a building also known as the ‘Water Cube’:

Let’s make that bigger:

It looks cool — and since I spent a lot of time on ‘spin foam’ models of quantum gravity, I instantly fell in love with it. But what’s so special about this structure?
In 1887, the physicist Kelvin asked how you can chop 3d space into cells of equal volume with the minimum surface area per cell. He conjectured that the answer was similar to a bitruncated cubic honeycomb — a way of filling space with truncated octahedra, like this:
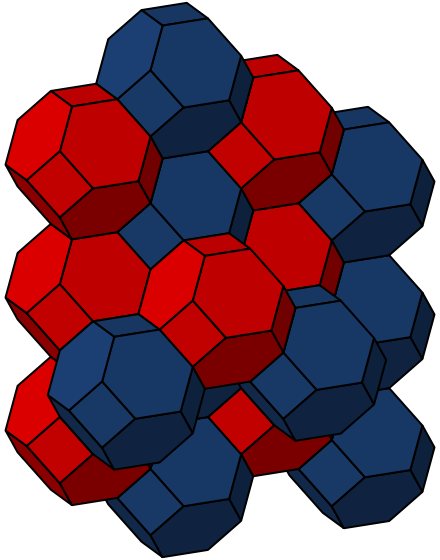
I say “similar” because it’s actually more efficient if you let the hexagonal faces in this structure be slightly curved. Kelvin wrote:
No shading could show satisfactorily the delicate curvature of the hexagonal faces, though it may be fairly well seen on the solid model made as described in Section 12. But it is shown beautifully, and illustrated in great perfection, by making a skeleton model of 36 wire arcs for the 36 edges of the complete figure, and dipping it in soap solution to fill the faces with film, which is easily done for all the faces but one. The curvature of the hexagonal film on the two sides of the plane of its six long diagonals is beautifully shown by reflected light.
Anyway, for over a century this so-called ‘Kelvin structure’ was believed to be the best solution to Kelvin’s problem. But in 1993, two physicists at Trinity College in Dublin — Denis Weaire and Robert Phelan — found a solution that has 0.3% less surface area! It looks like this:
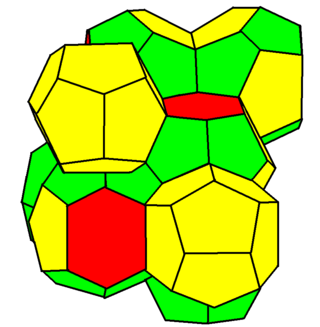
It’s built from two kinds of cells — a 12-sided one and a 14-sided one. Was that allowed in Kelvin’s original puzzle? I’m not sure!
This so-called Weaire–Phelan structure is perfectly periodic, though the cells are rather irregular in shape. To make it look more irregular, the structural engineer for the Water Cube building cut it at an odd angle.
From the Mathematical Association of America:
Made of a plastic known as ethylene tetrafluoroethylene and filled with air, the bubbles are attached to a steel framework outlining the bubble edges. Surface tension holds the bubbles together and tends to pull them into a structure with least surface area.
The building “really looks like nothing else in the world,” Tristam Carfrae told the New York Times. “It’s a box made of bubbles.” Carfrae is the structural engineer who designed the center.
Nobody has proved that the Weaire–Phelan structure is the best solution to Kelvin’s problem. But, it’s nice.

Re: The Weaire–Phelan Structure
The deformation of the bitruncated cubic honeycomb into a minimal surface is called the Schwarz P-surface. A cool property is self-complementarity, which the honeycomb also has.
The Schwarz P-surface has constant mean curvature. But there is also a related surface with constant Gaussian curvature, shown below:

The centers of the hyperbolic hexagons do not have an extrinsic curvature, although their intrinsic (Gaussian) curvature is well defined. This is why the surface does not violate Hilbert’s theorem that no complete regular C2 embedding of a hyperbolic suface exists.
I beleve it also self-complementary (see this page for more pictures.)
Gerard