But now, I want to give a definition of *-autonomous categories,
which simultaneously makes it clear that they’re natural structures
in logic, and that they’re categorified Frobenius algebras!
Suppose A is any category. We’ll call its objects
“propositions” and its morphisms “proofs”.
So, a morphism
f: a → b
is a proof that a implies b.
Next, suppose A is a symmetric monoidal category and call the tensor
product “or”. So, for example, given proofs
f: a → b, f’: a’ → b’
we get a proof
f or f’: a or a’ → b or b’
Next, suppose we make the opposite category Aop into a
symmetric monoidal category, but with a completely different tensor
product, that we’ll call “and”. And suppose we have a
monoidal functor:
not: A → Aop
So, for example, we have
not(a or b) = not(a) and not(b)
or at least they’re isomorphic, so there are proofs going both ways.
Now we can apply “op” and get another functor I’ll also call
“not”:
not: Aop → A
Using the same name for this new functor could be confusing, but it
shouldn’t be. It does the same thing to objects and morphisms; we’re
just thinking about the morphisms as going backwards.
Next, let’s demand that this new functor be monoidal! This too is
quite reasonable; for example it implies that
not(a and b) = not(a) or not(b)
or at least they’re isomorphic.
Next, let’s demand that this pair of functors:
not
--------->
A A^{op}
<----------
not
be a monoidal adjoint equivalence. So, for example, there’s a
one-to-one correspondence between proofs
not(a) → b
and proofs
not(b) → a
Now for the really fun part.
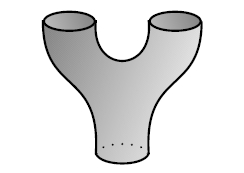
Let’s define a kind of “bilinear form”:
g: A × A → Set
where g(a,b) is the set of proofs
not(a) → b
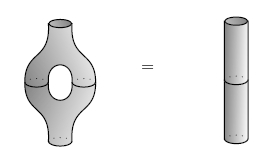
And let’s demand that g satisfy the Frobenius
axiom! In other words, let’s suppose there’s a natural
isomorphism:
g(a or b, c) ≅ g(a, b or c)
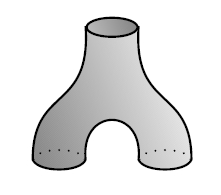
Then A is a “*-autonomous category”! And this is
a sensible notion, since it amounts to requiring a natural
one-to-one correspondence between proofs
not(a or b) → c
and proofs
not(a) → b or c
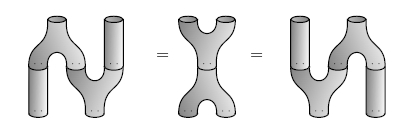
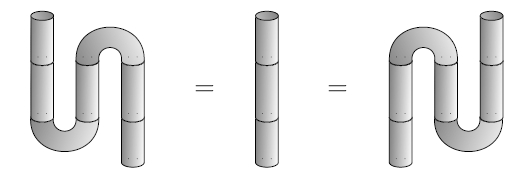
So, categorified Frobenius algebras are a nice framework for
propositional logic!
In case it slipped by too fast, let me repeat the definition of
*-autonomous category I just gave. It’s a symmetric monoidal
category A with a monoidal adjoint
equivalence called “not” from A (with one tensor product,
called “or”) to Aop (with another, called
“and”), such that the functor
g: A × A → Set
(a,b) |→ hom(not(a),b)
is equipped with a natural isomorphism
g(a or b, c) ≅ g(a, b or c)
I hope I didn’t screw up. I want this definition to
be equivalent to the usual one,
which was invented by Michael Barr quite a while ago:
27) Michael Barr, *-Autonomous Categories, Lecture Notes in
Mathematics 752, Springer, Berlin, 1979.
By now *-autonomous categories become quite popular among those
working at the interface of category theory and logic. And, there
are many ways to define them. Brady and Trimble found a nice one:
28) Gerry Brady and Todd Trimble, A categorical interpretation
of C. S. Peirce’s System Alpha, Jour. Pure Appl. Alg. 149
(2000), 213-239.
Namely, they show a *-autonomous category is the same as a symmetric monoidal category A equipped with a contravariant adjoint equivalence
not: A → A
which is equipped with a “strength”, and where the unit and counit of the adjunction respect this strength.
Later, in his paper “Frobenius monoids and pseudomonads”, Street
showed that *-autonomous categories are precisely Frobenius
pseudomonoids in a certain monoidal bicategory with:
-
categories as objects;
-
profunctors (also known as distributors) as morphisms;
-
natural transformations as 2-morphisms.
Alas, I’m too tired to explain this now! It’s a slicker way of saying what I already said. But the cool part is
that this bicategory is like a categorified version of Vect, with
the category of finite sets replacing the complex numbers. That’s
why in logic, the “nondegenerate bilinear form” looks like
g: A × A → Set






Re: This Week’s Finds in Mathematical Physics (Week 268)
Thanks for another intriguing article!
I found a few typos:
“3) [Jame|Jamie] Vicary, Categorical formulation”
“12) Marcelo Aguiar” - your previous reference was numbered 16. Subsequent references carry on from 13.
“some books on math and [musics|music]”