The n-Category Café

Isn’t that similar to zeta function regularization method? Every push forwared would be equivalent to a term of a Dirichlet series.

`Push forward of functors’ being Kan extension…

There is certainly a neat little story connecting this construction with (co)ends and indexed/weighted (co)limits.

I’ll talk about colimits; of course you can dualise everything if you care about limits instead. As David Roberts just mentioned, what you’re saying is that the colimit of your $F$ is the left Kan extension of F along the functor $p:A\to \{\mathrm{pt}\}$.

If we take $B$ to be (sufficiently) cocomplete, we can use the coend formula for left Kan extension: in general, the left Kan extension of $F:A\to B$ along $K:A\to X$ is

Now, the weighted colimit of $F:A\to B$ with weight $W:A^{\mathrm{op}}\to \mathrm{Set}$ is

So for each object $X\in X$, the object $({\mathrm{Lan}}_{K}F)(X)\in B$ is the weighted colimit

Thus in some sense the left Kan extension is a special case of the general notion of weighted colimit (and dually the right Kan extension is a special case of weighted limit).

Thanks David and Robin!

I am feeling somewhat stupid for not having realized this relation to coends (and not remembered it from the standard textbooks) – but better late than never.

I was reading Kelly’s book yesterday (without making it to page 64 – obviously :-/ – but still need to acquaint myself better with coends.

Here is a toy example that I should sit down and apply the coend formulation of the push-forward to:

Take the enrichment category to be the 1-category of categories, $V=\mathrm{Cat}$ so that a $V$-category is a strict 2-category.

Let $X$ be the 2-category

$$X=\{x\to y\leftarrow x\prime \}$$ (so that happens to be just a 1-category).

Let $\mathrm{phas}$ be the 2-category $$\mathrm{phas}:=B\mathrm{FinSet}$$ i.e the one-object 2-category whose Hom-category is $\mathrm{FinSet}$ and where composition is the cartesian product on sets.

Let $\Sigma$ be just the interval $$\Sigma :=\{a\to b\}.$$

Let $$F:X\to \mathrm{phas}$$ be a $V$-functor (i.e. strict 2-functor) and write $${\mathrm{ev}}^{*}F:\mathrm{hom}(\Sigma ,X)\times \Sigma \stackrel{\mathrm{ev}}{\to }X\stackrel{F}{\to }\mathrm{phas}.$$

I am after the pushforward of ${\mathrm{ev}}^{*}F$ down to $\Sigma$ along the canonical projection $$\mathrm{hom}(\Sigma ,X)\times \Sigma \to \Sigma$$ and its expression in terms of (co)ends.

Such will be the kind of exercise for my train ride tonight.

I should have made it clearer that I’ve been assuming that phas is (enriched) cocomplete.

Then the Kan extension $L:\Sigma \to \mathrm{phas}$ is given by the coend

By the Fubini theorem, this is isomorphic to

which is isomorphic to

by the density formula (aka the coend form of the Yoneda lemma). That’s the derivation of the claim I made yesterday. Since $f$ appears only once, and covariantly, this coend is just an ordinary colimit.

With your revised $X$, this colimit is a pushout.

(I can’t pretend that I’ve followed the back-story very clearly, so this observation may or may not be helpful.)

For the record and for my own benefit, I’ll review and summarize some of the enriched category theory aspects appearing in the above discussion (many thanks to Robin Houston for the help he provided!!), and pointing out where it says what in Kelly’s book:

G. M. Kelly, Basic concepts of enriched category theory

There are several directions from which to approach the generalization of ordinary (co)limits known as indexed (co)limits and as (co)ends. I’ll do it in a fashion somewhat reverse to how Kelly presents it:

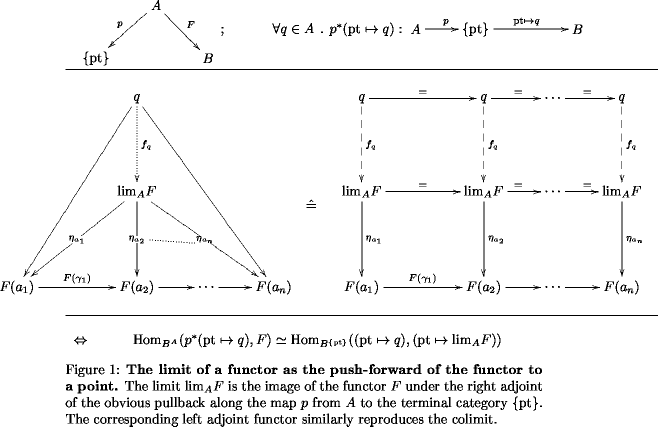
For me the starting point is the observation (section 3.4) that a cone over a functor

$$G:K\to B$$

with tip $b\in B$ usually thought of as a a transformation from the constant functor $\Delta b$ with value the tip $b$ into the functor G

$$\mathrm{Cone}(b,F)\in [K,B](\Delta b,G),$$

where $$\Delta b:K\to \{\mathrm{pt}\}\stackrel{\mathrm{pt}\mapsto b}{\to }B,$$

can equivalently be thought of as a cone in “copresheaves” on $K$, with tip the constant functor $\Delta 1$ at the singleton set:

$$[K,B](\Delta B,G)\simeq [K,\mathrm{Set}](\Delta 1,B(b,G(-))).$$

I suppose one way to motivate indexed limits is to observe that in the formulation on the right hand, as opposed to the one on the left hand, there is a singled out functor appearing, namely

$$\Delta 1:K\to \{\mathrm{pt}\}\stackrel{\mathrm{pt}\mapsto \{•\}}{\to }\mathrm{Set}.$$

Therefore it is natural to generalize the notion as it appears on the right, by replacing this constant functor with something else.

And indeed, that’s what one does:

we allow $\mathrm{Set}$ to be replaced by any other enriching category $V$ (I won’t try to list all the properties we need on $V$ to make each an all of the following constructions possible) and generalize $$[K,\mathrm{Set}](\Delta 1,B(b,G(-)))$$ first to $$[K,V](\Delta I,B(b,G(-)))$$ and then to $$[K,V](F,B(b,G(-))),$$ where now $$F:K\to V$$ can by any functor, not necessarily one constant at the tensor unit object.

(Now I am on p. 37, equation (3.1).)

Instead of saying then that the cone is indexed by $K$, we say that it is indexed by $F$ (which includes the information about $F$’s domain $K$, of course).

Now, a limit of a functor $G$ is something that represents the universal cone over $G$, in that morphisms into the limit are in bijection with cones over the functor.

So we do the same here and define the limit of $G$ indexed by $F$, what you might denote ${\lim }_{F}G$, by the property

$$B(b,{\lim }_{F}G):\simeq [K,V](F,B(b,G(-)))$$

naturally for all $b\in B$.

Only that, for some reason, one invents completely unsuggestive new notation and writes $\{F,G\}$ for what I called ${\lim }_{F}G$ above. So this should really read:

$$B(b,\{F,G\}):\simeq [K,V](F,B(b,G(-))).$$

For indexed colimits the discussion is the same with both (!) $K$ and $B$ replaced by their opposite categories. (equation 3.5, p. 38).

The $F$-indexed colimit ${\mathrm{colim}}_{F}G$ over $G$ also receives its own notation: $F\star G$:

$$B(F\star G,b):\simeq [K^{\mathrm{op}},V](F,B(G(-),b)).$$

A most important special case of such indexed (co)limits is that where we can think of them as weighted (co)limits, a situation which is the basis for a striking similarity between indexed colimits and the theory of ordinary integration (as in functional analysis).

That special case is that where the codomain of our functor is (co)tensored over the enriching category. (section 3.7, p. 48)

A $V$-category $B$ being tensored over $V$ is much like a “$V$-module”: $V$ behaves like a monoid which acts on $B$. Or more suggestively, $B$ behaves like a vector space over $V$.

(Here is a question: is there a difference between saying that $B$ is tensored over $V$ and looking at $V$ as a monoid in $V$-Cat and at $B$ as a module for that monoid in $V$-Cat?)

If $B$ is tensored over $V$ one writes (this time the notation is natural)

$$v\otimes b$$

for the result of acting with $v\in V$ on $b\in B$.

(The notation for the cotensor product, on the other hand, I can’t even typeset here without looking up special character tables…)

The punchline now is that if $B$ is tensored over $V$, the $(F:K\to V)$-indexed colimit over a functor $G:K\to B$ can be expressed by a coend over the tensor product:

$${\mathrm{colim}}_{F}G:=F\star G\simeq {\int }^{k\in K}F(k)\otimes G(k).$$

(equation 3.70, p. 53)

So now I say what what a coend is, the thing appearing on the right hand here:

Where indexed (co)limits generalized ordinary (co)limits by generalizing what we may regard as the tip of a cone, (co)ends generalize ordinary (co)limits by generalizing what the functor we take the limit over may be: namely from the case of functors on $K$ to functors on $K^{\mathrm{op}}\times K$.

One way to motivate this is by thinking about what natural transformations really are:

given two ordinary functor:

$$T,S:A\to B$$

a natural transformation $\eta :T\Rightarrow S$ is, for each $a\in A$ a map $${\eta }_a:I\to B(T(a),S(a))$$ namely a morphism in $B$, such that all naturality squares commute, which in terms of this map means that for all $f:a\to b$ in $A$ we have

$$\begin{array}{ccc}I& \stackrel{{\eta }_a}{\to }& B(T(a),S(a))\\ {\downarrow }^{{\eta }_b}& & {\downarrow }^{B(T(a),S(f))}\\ B(T(b),S(b))& \stackrel{B(T(f),S(b))}{\to }& B(T(a),S(b))\end{array}.$$

The point to notice is that in the special case that the functor $T$ is trivial this reduces precisely to a cone over the functor $B(T,S(-)):A\to B$. So the naturality of natural transformations is a generalization of the notion of cone to functors with a covariant and a contravariant dependence on their domain category.

As the vertical morphisms of a cone form a natural family of morphisms with respect to the functor that the cone lives over, the morphisms ${\eta }_a:I\to B(T(a),S(a))$ of a natural transformation form what is called an extraordinary natural family (1.7, p. 17).

Generally, then, this is the definition of an end: not just a universal natural family of morphisms (that would be a limit), but a universal extraordinary natural family.

More precisely for a functor $$T:A^{\mathrm{op}}\times A\to V$$ a (extraordinary) natural family of morphisms from some object $k\in V$ $${\lambda }_a:k\to T(a,a)$$ for all $a\in A$ is one for which for all $f:a\to b$ in $A$ we have: $$\begin{array}{ccc}K& \stackrel{{\lambda }_a}{\to }& T(a,a)\\ {\downarrow }^{{\lambda }_b}& & {\downarrow }^{T(a,f)}\\ T(b,b)& \stackrel{T(f,b)}{\to }& T(a,b)\end{array}.$$ Or rather, this is the condition when it makes sense to speak of morphism in $A$, as when $V=\mathrm{Set}$. More generally one reformulates this into a more robust (but less enlightning on first sight) way which works for all enrichment categories. See equation 1.40 on p. 18.

Then (p. 27) the end

$${\int }_{A}T:={\int }_{a\in A}T(a,a)$$

over a functor $T:A^{\mathrm{op}}\times A\to V$ is the (domain object of the) universal such natural family, in that every other one factors through it.

We get from this back to the motivating example of natural transformations by now noticing that this gives a way to speak of the $V$-object of natural transformations in any enriched context (2.2, p. 29): the $V$-object of natural transformations of $V$-functors $T,S:A\to B$ is defined by the end over the functor $B(T(-),S(-))$

$$[A,B](T,S):={\int }_{a\in A}B(T(a),S(a)).$$

Finally, now, we get to coends, by dualizing ends: the coend ${\int }^{a\in A}G(A,A)$ is defined by (3.67, p. 53) $$B({\int }^{a\in A}G(a,a),b)\simeq {\int }_{a}B(G(a,a),b)$$ naturally for all $b\in B$.

Just as ends over $T:A^{\mathrm{op}}\times A\to V$ reduce to limits when there is no dependency of $T$ on the first (contravariant) variable of $T$, coends reduce to colimits in the same case.

To get an intuition for what is going on with our formula for the $F$-indexed colimit over $G$

$$F\star G\simeq {\int }^{k\in K}F(k)\otimes G(k)$$

it is helpful to consider the special simple case that John described here:

suppose that $V=\mathrm{FinSet}$ such that isomorphism classes in $V$ are given by natural numbers and such that coproduct induced addition of these natural numbers.

Let $A=\mathrm{Disc}(X)$ be the discrete $V$-category over a set $X$: all Hom-objects are trivial.

Moreover, let $B=\mathrm{SetMod}$, the category whose objects are categories with a $\mathrm{Set}$-action on them and whose morphisms are $\mathrm{Set}$-linear functors between these.

(I am hoping that I am right that this $B$ is $\mathrm{Set}$-tensored. If not, just take $B=\mathrm{Set}$ instead in the following.)

Then a functor $$G:A\to B$$ i.e $$G:X\to \mathrm{SetMod}$$ is like a vector-valued function on the set $X$, and a functor $$F:X\to \mathrm{Set}$$ is like a number-valued function on $X$. And $$F(-)\otimes G(-)$$ is like a vector valued function on $X$ obained by multiplying $G$ pointwise by $F$.

Moreover, the coend $${\int }^{x\in X}F(x)\otimes G(x)$$ reduces to just to coproduct $${\oplus }_{x\in X}F(x)\otimes G(x).$$ This is just like the integral of $G$ over $X$ weighted by $F$.

It is amazing how close the notion of coends, and also the notation used, is to ordinary integration theory. But the notation is not perfect. First of all it is a pity that the coend has the integration bounds on top instead of at the bottom of the integral sign. It should be the other way around.

If I had to make up notation from scratch, I’d opt for writing the coend of a functor $G$ with values in a $V$-tensored category $B$ with weight $F$ as

$${\int }_{X}Gd{\mu }_F.$$

Moreover, if products and coproducts coincide, such as in $\mathrm{FinVect}$, I’d write (along the lines of John Baez, of course) $$\langle a,b\rangle :=B(a,b)$$ for $a,b\in B$, which would turn formulas such as 3.67 into pleasant familiar formulas such as $$\langle {\int }_{X}Gd{\mu }_F,b\rangle ={\int }_X\langle G,b\rangle d{\mu }_F.$$