Theorems Into Coffee IV

July 12, 2008

Posted by John Baez

$MathML-enabled post (click for more details).$

I’m in Paris now. I’ve spent this week attending a conference on Algebraic Topological Methods in Computer Science. Yesterday during one of the breaks my host, Paul–André Melliès, introduced me to a student I’d seen somewhere before. I didn’t catch the guy’s name, but his eyes glittered strangely as we sipped our coffee and talked, and then I realized: it was Samuel Mimram, winner of the first Theorems Into Coffee challenge! In this paper:

Samuel Mimram, Presentation of a game semantics for first-order propositional logic, Thm. 14, page 22.

he proved the result I sought, namely:

Theorem: $Mat(\mathbb{N})$ is the PROP for bicommutative bimonoids.

So, I handed him an elegant handmade Korean envelope containing 20 euros — to be spent only on coffee.

$MathML-enabled post (click for more details).$

I’m not sure how my offered prize of 15 dollars turned into 20 euros. I must have been in a good mood.

Earlier at the same conference I spoke to Eugenia Cheng about her work on the Theorems into Coffee problems, and we wound up studying this paper by Steve Lack:

Steve Lack, Composing PROPs, Theory and Applications of Categories 13 (2004), 147–163.

Abstract: A PROP is a way of encoding structure borne by an object of a symmetric monoidal category. We describe a notion of distributive law for PROPs, based on Beck’s distributive laws for monads. A distributive law between PROPs allows them to be composed, and an an algebra for the composite PROP consists of a single object with an algebra structure for each of the original PROPs, subject to compatibility conditions encoded by the distributive law. An example is the PROP for bialgebras, which is a composite of the PROP for coalgebras and that for algebras.

It’s very nice, and Lack probably deserves several kilos of coffee. Let me quickly sketch some of his results before proposing the next Theorems Into Coffee problem.

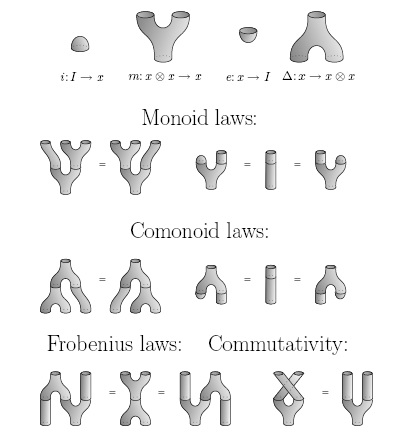
I’ve already explained PROPs and their algebras, but let me remind you of the official definition:

Definition: A PROP is a strict symmetric monoidal category $X$ with natural numbers as objects, for which the tensor product of objects $n$ and $m$ is $n + m$ . Given a symmetric monoidal category $C$ , an algebra of $X$ in $C$ is a symmetric monoidal functor $F: X \to C$ , and a morphism of algebras is a symmetric monoidal natural transformation between such functors. There is a category of algebras of $X$ in $C$ .

However, it’s sometimes convenient to relax our definition a bit and consider any symmetric monoidal category that’s equivalent to a PROP to again be a PROP. This amounts to saying:

Definition: A relaxed PROP is a symmetric monoidal category $X$ with an object $x$ such that every object is isomorphic to one of the form $x \otimes \cdots \otimes x$ .

If we then define algebras and morphisms between algebras as before, it’s clear that for every relaxed PROP there is a PROP with an equivalent category of algbras. So, we’re not losing anything, or gaining anything… except that sometimes it’s easier or more fun to describe the relaxed version of a PROP.

For example, I’ve already mentioned a PROP called $Mat(\mathbb{N})$ , where the morphisms from $n$ to $m$ are $m \times n$ matrices of natural numbers, and composing morphisms is done by matrix multiplication. This is nice, but there’s a more conceptual way to think about it as a relaxed PROP: namely, the category where the objects are finite sets, the morphisms are spans of finite sets, and we compose spans by pullback. I call this category $Span(FinSet)$ .

(Actually, to be perfectly honest, I’ve just described a bicategory rather than a category, since composition of spans is associative only up to isomorphism! But we can take isomorphism classes of spans and get a category — and that’s what I’ll do. So, just for today, I’m secretly using ‘span’ to mean ‘isomorphism class of span’.)

In Section 5.3 of his paper, Steve Lack proves a result equivalent to Samuel Mimram’s result mentioned above:

Theorem: $Span(FinSet)$ is the relaxed PROP for bicommutative bimonoids.

By this I mean that the category of algebras of $Span(FinSet)$ in any symmetric monoidal category $C$ is equivalent to the category of bicommutative bimonoids in $C$ .

The interesting thing is that Lack has a very conceptual way to prove this sort of result, not involving string diagrams (as in Mimram’s proof) or matrices (as in Simon Wadsley’s). Instead, he uses a way of tensoring two PROPs given a rule that says how to slide operations of one past operations of the other. This rule should probably be called a ‘commutative law’ or ‘braiding’, but the term ‘distributive law’ is traditional, since the old-fashioned distributive law

$a(b + c) = a b + a c$

is an example: it tells you how to switch from adding first and then multiplying to multiplying first and then adding!

In particular, Lack starts by proving this:

Theorem: $FinSet$ is the relaxed PROP for commutative monoids.

where $FinSet$ is the category of finite sets and functions. It’s then easy to see:

Theorem: $FinSet^{op}$ is the relaxed PROP for cocommutative comonoids.

Then, using a certain distributive law to tensor these two PROPs, he shows

Theorem: $FinSet^{op} \otimes FinSet \simeq Span(FinSet)$ is the relaxed PROP for bicommutative bimonoids.

Even if you don’t quite follow what’s going on, this should have a ring of plausibility. Every operation $f : A^{\otimes m} \to A^{\otimes n}$ for a bicommutative bimonoid $A$ can be achieved by first doing a bunch of comultiplications and then a bunch of multiplications. Similarly, every span in $FinSet$ looks like this:

$X \leftarrow S \rightarrow Y$

so we’re first doing a morphism in $FinSet^{op}$ and then a morphism in $FinSet$ . A morphism in $FinSet^{op}$ is just what we need to describe a bunch of comultiplications; a morphism in $FinSet$ is just what we need to describe a bunch of multiplications!

Charmingly, Lack also shows:

Theorem: $FinSet \otimes FinSet^{op} \simeq Cospan(FinSet)$ is the relaxed PROP for commutative separable algebras.

If I remember correctly, a separable algebra $A$ is one where the bilinear form $\langle a, b \rangle = tr(L_a L_b)$ is nondegenerate, where $L_a$ means left multiplication by $a$ . This makes $A$ into a Frobenius algebra with the special property that comultiplication followed by multiplication is the identity!

So, a commutative separable algebra is a specially nice Frobenius algebra — maybe just a commutative Frobenius algebra where comultiplication followed by multiplication is the identity.

Note: I’ve slipped into terminology that people use in the category of vector spaces, like calling a monoid an ‘algebra’. But, everything I’m saying makes sense in any symmetric monoidal category. So, you might prefer to cross out ‘algebra’ wherever you see it, and write in ‘monoid’. Go ahead — just don’t damage your computer screen!

But the point is this:

It’s really easy for beginners to get mixed up between bialgebras and Frobenius algebras, since they both have a multiplication and comultiplication, and some classic examples, like the group algebra of a finite group, are both bialgebras and Frobenius algebras. Now we’re seeing a deep relationship between the two, which shows that the beginner’s confusion is not purely stupid.

(There’s at least one other deep relationship, too. A bialgebra may be defined as an algebra that’s also a coalgebra, such that all the coalgebra operations are algebra homomorphisms. A Frobenius algebra $A$ may be defined as an algebra that’s also a coalgebra, such that all the coalgebra operations are $A,A$ -bimodule homomorphisms!)

Lack also describes the PROP for bialgebras… or, if you prefer, bimonoids. This was going to be my next coffee problem, since James Dolan and I had worked out this PROP after quite a bit of struggle and confusion, and I wanted someone to give a nice proof. Here’s the answer:

First, let $P$ be the relaxed PROP where the objects are finite sets and the morphisms are functions where each fiber is equipped with a linear ordering. Lack shows:

Theorem: $P$ is the relaxed PROP for monoids.

The point is that we don’t know how to multiply a bunch of guys in a monoid unless we know what order they’re in. Similarly:

Theorem: $P^{op}$ is the relaxed PROP for comonoids.

and using a certain distributive law to tensor the two:

Theorem: $P^{op} \otimes P$ is the relaxed PROP for bimonoids.

This PROP is a bit strange. A morphism in this PROP is just a span in $P$ , but we don’t compose these spans by pullback! Instead, we need to insert a ‘fiendish twist’. You can see this as a permutation called $\pi$ in the very last diagram of Lack’s paper — a permutation that turns the usual pullback square into a pentagon.

This fiendish twist arises from the fact that there are two natural ways to make the cartesian product of totally ordered sets into a totally ordered set: the lexicographic ordering and the reverse lexicographic ordering.

And, it’s this ‘fiendish twist’ that’s the really interesting thing about the PROP for bimonoids. It gave James and Eugenia and me many hours of suffering and delight!

Alas, I’m getting too worn out to explain it properly here, so let me just say this: Ponder the PROP for bimonoids, try to describe it as above, think about how to compose the operations, and you will discover the fiendish twist.

Now let me pose the fourth Theorems Into Coffee problem — for a prize of 15 dollars worth of coffee, under the usual terms and conditions:

Coffee Problem: Give an elegant description of the PROP for Hopf algebras.

This is more open-ended than the previous ones…

Posted at July 12, 2008 1:30 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1740

27 Comments & 0 Trackbacks

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Here’s another question: what about $P\otimes P^{op}$ ?

(I should admit that what I’m calling $P$ , Lack calls $P \otimes D$ , written in blackboard bold.)

Posted by: John Baez on July 12, 2008 2:13 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

I had a question about rewriting systems that I will pretend is on topic, since “rewriting systems” appear on the list of topics for the conference.

In a computer program, you want to think of rewrite rules as going in one direction to avoid looping, but in a pure mathematical sense, rewrite rules are bidirectional, and just represent generators of an equivalence relation. In that context, what is the next higher-level concept? I assume something corresponds to an “equivalence relation between equivalence relation”. I started working this out, but it gave me a headache. I assume someone has worked it out already.

Posted by: Walt on July 12, 2008 10:35 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Aha.

For the answer to your question, you should have been at ATMCS with John and myself.

This has been worked on, but first I should point out that there are LOTS of pure mathematical situations where rewriting is not bidirectional and in fact even in the theory of groups presentations, and in its computational form, (computational groups theory), it is quite usual for people to use a presentation with paired generators, each pair thought of as $(x,x^{-1})$ with a rewrite to 1 included in the relations and that rewrite cannot be reversible as it destroys information. Rewriting also comes into the various ways of presenting the lambda calculus and that is one of the reasons why Paul-André Melliès and others are interested in it. There is also a link with the theory of locally directed spaces which looks to be a very subtle one, but could be very interesting,

The higher dimensional theory you ask about exists in several forms. One of the neatest is the theory of polygraphs which extend the computads of Street. There were several talks on that subject (the program of ATMCS is available with the abstracts from the conference website, and Eric Goubault hopes to have most of the slides used available there sometime next week…. but I did not use slides for my talk! Chalk and talk for ever.) For the rewriting aspects, one of the talks was by Philippe Malbos, and he dealt with Higher-dimensional categories with finite derivation type which topic could be very useful for the denizens of the café.

Needless to say, the conference was also very good for the food but that is another matter.

Posted by: Tim Porter on July 13, 2008 9:27 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

Tim Porter wrote:

For the rewriting aspects, one of the talks was by Philippe Malbos, and he dealt with Higher-dimensional categories with finite derivation type which topic could be very useful for the denizens of the café.

Thank you Tim for advertising our work. For denizens of the café that might be interested, the slides of Philippe’s talk are now available on his page or mine.

We are currently working to finish the corresponding paper to make it available on the arXiv in the coming weeks.

Posted by: Yves Guiraud on July 15, 2008 3:27 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Walt wrote:

In a computer program, you want to think of rewrite rules as going in one direction to avoid looping, but in a pure mathematical sense, rewrite rules are bidirectional, and just represent generators of an equivalence relation.

As Tim noted, it depends what you want: sometimes it’s good to think of rewrite rules as reversible, but other times it’s good to think of them as having a specified direction. If they’re reversible you get a groupoid — and a groupoid with at most one morphism from one object to another is called an ‘equivalence relation’. If they’re directional you get a category — and a category with at most one morphism from one object to another is called a ‘preorder’… the most famous special case being a ‘poset’.

To discuss ‘terminating and confluent rewrite rules’, we need the rules to be directional.

In that context, what is the next higher-level concept? I assume something corresponds to an “equivalence relation between equivalence relation”.

Right! The old-fashioned name is ‘syzygy’, or ‘relation between relations’. In the old days, pondering these led people to invent homological algebra.

You have an algebraic gadget with some generators and relations, but then sometimes you discover there are relations between relations: two different ways to use the relations to prove the same equation! And then you discover relations between relations between relations, and so on, ad infinitum.

If you treat all these relations between relations between relations as reversible, you get an $\infty$ -groupoid — but the simplest example is a strict $\infty$ -groupoid in the category of abelian groups, and the old-fashioned name for that is ‘chain complex’. This chain complex is called a ‘resolution’ of your original algebraic gadget: it’s a puffed up version where we’re repeatedly replaced equations between $n$ -isomorphisms by $(n+1)$ -isomorphisms.

Then we can use this resolution to apply topological ideas, like cohomology, to our algebraic gadget.

You can read a lot about this in my Spring 2007 seminar. My goal there was to very explicitly make the connection between the $n$ -categorical ideas and the old ideas about syzygies and cohomology. But, I didn’t get as far as I might have wanted.

To go further, I urge you to learn about Craig Squier’s famous theorem relating homology of monoids to the word problem for monoids. You can read an expository account in week70, and then for more details, the paper by Lafont and Prouté referred to there. Since then Lafont and others have gone much further relating rewriting theory, $n$ -categories and homology. It’s great stuff!

Posted by: John Baez on July 13, 2008 10:42 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

Thanks for the links! I’m reading them now.

Posted by: Walt on July 14, 2008 4:06 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

By the way: if you’re left wondering what all the stuff in those links has to do with $n$ -categories, the missing piece is a certain fact I alluded to:

A strict $\infty$ -groupoid internal to the category of abelian groups is the same as a chain complex.

This is a close relative of the Dold–Kan theorem:

An abelian group internal to the category of simplicial sets is the same as a chain complex.

Indeed, if you’re happy with simplicial methods, $\infty$ -categories are overkill for what I’ve described so far, so you can ignore them.

On the other hand, $\infty$ -categories become crucial here.

Posted by: John Baez on July 14, 2008 4:43 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

On the other hand, $\infty$ -categories become crucial here.

From slide 64 on this mentions A folk model structure on $\omega$ Cat, whose existence I am enjoying a lot.

The weak equivalences are $\omega$ -functors $C \to D$ which are essentially $k$ -surjective for all $k \in \mathbb{N}$ in the sense of your lecture on cohomology. (Do you mention that relation to weak equivalences? Maybe you do, but it was only after reading the “folk model” article that I got it).

This notion of weak equivalence is extremely useful for instance when handling strict $\infty$ -groups. Is this mentioned in the context of Behrang’s “butterfly” morphisms? (Didn’t yet find the time to look at that in any detail.)

Posted by: Urs Schreiber on July 14, 2008 6:47 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Is this mentioned in the context of Behrang’s “butterfly” morphisms?

not as far as I could tell. The butterfly morphisms are closer to a localisation - I haven’t worked out the details, but it looks to me that given the (2-)category of crossed modules and strict maps (respecting products on the nose), enough is localised so that the resulting 2-category is equivalent to the 2-category of 2-groups and weak maps between them (respecting the product weakly and all that jazz).

The “localisation”, if that is what it is, is more like Hilsum-Skandalis (but a 2-category version) in that the maps are not spans of objects (say like Pronk), but some sort of bibundle, of which one side is principal. Since we are working internal to groups, a principal bundle is nothing other than an extension of groups, and the ‘non-principal bundle’ is a complex of groups.

If you wanted to recover the span-type version, one could induce a crossed module from $G_1 \to G_2$ given the surjective map of groups $E \to G_2$ . Using the various maps of the butterfly one should be able to show that this new crossed module is weakly equivalent to the domain crossed module. Just a thought.

If you are thinking of $\infty$ -groups as reduced ( $=$ ‘one-object’) simplicial objects, then I’m not sure how to implement a Noohi-style approach, since that is very much from the ‘internal groups’ POV.

Posted by: David Roberts on July 15, 2008 5:10 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

David R. wrote:

it looks to me that given the (2-)category of crossed modules and strict maps (respecting products on the nose), enough is localised so that the resulting 2-category is equivalent to the 2-category of 2-groups and weak maps between them (respecting the product weakly and all that jazz).

Let me try to say that in terms of the “folk” model category structure on $\omega\mathrm{Cat}$ :

the weak equivalences are the $\omega$ -functors $C \stackrel{\simeq_w}{\to} D$ which are essentially $k$ -surjective for all $k$ .

Crossed modules are strict one-object 2-groupoids $\mathbf{B}G \in \omega\mathrm{Cat}$ .

Even though all morphisms in $\omega\mathrm{Cat}$ are strict $\omega$ -functors, this allows, it seems, to get weak 2-functors between strict 2-categories in terms of generalized morphisms

$\array{ & \hat C \\ & {}^{\simeq_w}\swarrow \searrow \\ C && D }$ by letting $\hat C$ be defined as follows:

its objects are those of $C$ , its morphisms are finite sequences of composable morphisms in $C$ , composition is concatenation of sequences. It has 2-morphisms generated from those of $C$ plus new ones generated from triangles $\array{ && b \\ & {}^f\nearrow & \Downarrow^{c_{c,g}}_\simeq& \searrow^g \\ a &&\stackrel{g \circ_C f}{\to}&& c }$ and their formal inverses, subject to the obvious associativity and co-associativity and “Frobenius”-constraints and the obvious compatibility with the original 2-morphisms.

The map $\hat C \stackrel{\simeq_w}{\to} C$ sends objects to obects, sequences of 1-morphisms to their composition in $C$ original 2-morphisms to themselves and the new 2-morphisms to identities.

The associativity and co-associativty and Frobenius conditions ensure that this is a weak equivalence.

Then strict 2-functors $\hat C \to D$ are in bijection with weak 2-functors $C \to D$ . It seems.

Posted by: Urs Schreiber on July 21, 2008 11:34 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

On the other hand, $\infty$ -categories become crucial here.

From slide 64 on this mentions A folk model structure on $\omega Cat$ , whose existence I am enjoying a lot.

Maybe somebody can help me with the following questions on A folk model structure on $\omega Cat$

a) The authors prove the model structure properties by checking that the hypothesis of “Smith’s theorem” are satisfied.

What is the reference for “Smith’s theorem”? They don’t give any.

b) Can anything be said in general about if and how the model structure on $\omega Cat$ would generalize to $\omega$ -categories internal to a topos other than $Sets$ ? In particular to $\omega$ -categories internal to a presheaf topos?

Posted by: Urs Schreiber on September 26, 2008 4:13 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

It seems to me that simplicial methods are just a tool at getting at something more basic. (For example, group cohomology is more than just the bar resolution.)

Posted by: Walt on July 14, 2008 7:46 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

More and less
It’s the homotopy type of the bar resolution that really matters.

Posted by: jim stasheff on July 15, 2008 1:20 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

A useful way to think of simplicial methods may be that they are often naturally there because of a comonad structure. They may not be optimal in a given context (and this is sometimes a question of taste). They do provide a large tool kit for analysis as there is usually a Quillen model category structure around to provide a quick route to some significant theorems. On the other hand they nearly always repeat information many times because of the decompositions of objects of simplices as `semidirect products’ of lower dimensional terms. (This comes from the fact that face maps are always split epimorphisms.)

In the Menagerie notes that John refered to I included a section on the geometric side of group presentation theory and how it interacts with simplicial (and to a limited extent categorical) considerations. It may help to glance at that… the key word is `syzygy.

When one gets to structure other than standard algebraic ones then the usefulness of simplicial methods does decrease.

One question I would like to ask of any computer science experts who read this blog is:

What is the significance of higher `identities between relations’ when looking at rewriting systems? This is to be seen as relating to 2-logic as in other threads. Reducing a term to normal form is clearly important, but what is the usefulness in `practice’ of knowing if it can be done in two different ways?

Posted by: Tim Porter on July 16, 2008 8:09 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

Tim Porter wrote:

One question I would like to ask of any computer science experts who read this blog is:

What is the significance of higher `identities between relations’ when looking at rewriting systems? This is to be seen as relating to 2-logic as in other threads. Reducing a term to normal form is clearly important, but what is the usefulness in `practice’ of knowing if it can be done in two different ways?

I may have two reasons but they come from a mathematician so I do not know if they qualify ;)

A first reason is that identities between relations can be used to design reduction strategies. This can be important because a given reduction path can be much more expensive to compute than another, parallel one. In that case, the programmer may want to specify that the computer should use the cheaper one: a way to do that is to give an explicit reduction strategy. This is already possible in programming languages such as Tom, thanks to a dedicated syntax.

But one can think of another way to specify a strategy. For that, I assume that the considered rewriting system is convergent (i.e. terminating and confluent). A strategy amounts at choosing, whenever one encounters two parallel reduction paths, one of them: from a topological point of view, this means filling the sphere they form with a directed cell. And all these spheres have the same generators as the module of identities between relations.

However, to produce a strategy, these choices must be made in a coherent way: one must be able to choose one path among three, four, five, etc. parallel ones. This means that one needs to fill the higher-dimensional spheres corresponding to identities between identities between identities etc. between relations, until one reaches some acyclic object (this object being a variant of polygraph). This is related to the notion of homotopical dimension of rewriting systems Philippe Malbos has mentioned during the ATMCS meeting.

This leads to a second reason to explore identities between relations: to design algorithmic invariants. Indeed, two programs may implement the same algorithm, yet they may differ synctactically (they may even be written in two different languages). However, their reduction spaces should be equivalent, in some topological way. For example, they should have the same homotopical dimension. Also, they should have the “finite derivation type” property at the same time, i.e. the two modules of identities between relations should be finitely generated at the same time.

Posted by: Yves Guiraud on July 16, 2008 10:59 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

Generic Commutative Separable Algebras and Cospans of Graphs might cast some light on separable algebras.

Looks like to follow the trail back you need A. Carboni, Matrices, relations and group representations, J. Algebra, 138, 497–529, 1991, and before this F. DeMeyer, E. Ingraham, Separable algebra over commutative rings, Springer Lecture Notes in Mathematics, 181, 1971.

Did you hear Walters’ talk at the StreetFest?

Posted by: David Corfield on July 14, 2008 8:43 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

David wrote:

Generic Commutative Separable Algebras and Cospans of Graphs might cast some light on separable algebras.

Good point! Yes, Prop. 3.1 of this paper shows that the category with finite sets as objects and cospans as morphisms is the PROP for ‘commutative separable algebras’.

Better still, they say what a commutative separable algebra is!

Such a gizmo, say $x$ , can live in any symmetric monoidal category. First, it’s a commutative Frobenius monoid — meaning it’s a commutative monoid with multiplication $m$ and unit $i$ :

$m : x \otimes x \to x,$ $i : I \to x$

that’s also a cocommutative comonoid with comultiplication $\Delta$ and counit $e$ :

$\Delta : x \to x \otimes x,$ $e : x \to I$

such that the Frobenius laws hold:

$(1_x \otimes m)(\Delta \otimes 1_x) = \Delta m = (m \otimes 1_A)(1_A \otimes \Delta)$

In terms of pictures, this means:

But then we have the all-important separability condition, which says that comultiplication followed by multiplication is the identity:

$m \Delta = 1_A$

In terms of pictures, this means

So, the category of cospans of finite sets is just like the category $2Cob$ , where morphisms are 2d cobordisms as shown in the pictures above… but with this extra relation:

which James Dolan calls ‘the genus-killer’.

It’s pretty easy to convince oneself that this is true, by drawing some pictures of cospans of finite sets.

David wrote:

Did you hear Walters’ talk at the StreetFest?

Yes, but there were over 60 talks at that conference…

Posted by: John Baez on July 21, 2008 12:06 PM | Permalink | Reply to this

Academy of Lagado; Re: Theorems Into Coffee IV

The humor (I use that term advisedly) of saying that “A Mathematician is a machine for turning coffee into theorems” is that, for the non-mathematician, a person is a machine for turning coffee into urine. What is interesting is that theorems and bodily fluids represent two different streams processed from the same input. One stream is flushed away; the other is published.

I am not trying to be funny here, or piss you off, but to seriously comment on the issues of duality from reversing the direction of arrows, and the plausibility of the term “Foundation” is Mathematics as derived from Architecture, with a theme common to Turning Theorems into Coffee and to Jonathan Swift’s deadly-accurate satire of academe in TRAVELS, PART III: A VOYAGE TO LAPUTA, BALNIBARBI, LUGGNAGG, GLUBBDUBDRIB AND JAPAN, Chapter V.

The Author permitted to see the grand Academy of Lagado. The Academy largely described. The Arts wherein the Professors employ themselves.

… His Employment from his first coming into the Academy, was an Operation to reduce human Excrement to its original Food, by separating the several Parts, removing the Tincture which it receives from the Gall, making the Odour exhale, and scumming off the Saliva. He had a weekly Allowance from the Society, of a Vessel filled with human Ordure about the Bigness of a Bristol Barrel.

I saw another at work to calcine Ice into Gunpowder; who likewise shewed me a Treatise he had written concerning the Malleability of Fire, which he intended to publish.

There was a most ingenious Architect who had contrived a new Method for building Houses, by beginning at the Roof, and working downwards to the Foundation; which he justified to me by the like Practice of those two prudent Insects, the Bee and the Spider.

There was a Man born blind, who had several Apprentices in his own Condition: Their Employment was to mix Colours for Painters, which their Master taught them to distinguish by feeling and smelling. It was indeed my Misfortune to find them at that Time not very perfect in their Lessons; and the Professor himself happened to be generally mistaken: This Artist is much encouraged and esteemed by the whole Fraternity….

There was an Astronomer who had undertaken to place a Sun-Dial upon the great Weather-Cock on the Town-House, by adjusting the annual and diurnal Motions of the Earth and Sun, so as to answer and coincide with all accidental Turnings of the Wind….

Project for improving speculative Knowledge by practical and mechanical Operations. But the World would soon be sensible of its Usefulness, and he flattered himself that a more noble exalted Thought never sprung in any other Man’s Head. Every one knew how laborious the usual Method is of attaining to Arts and Sciences; whereas by his Contrivance, the most ignorant Person at a reasonable Charge, and with a little bodily Labour, may write Books in Philosophy, Poetry, Politicks, Law, Mathematicks and Theology, without the least Assistance from Genius or Study. He then led me to the Frame, about the Sides whereof all his Pupils stood in Ranks. It was twenty Foot Square, placed in the middle of the Room. The Superficies was composed of several bits of Wood, about the bigness of a Dye, but some larger than others. They were all linked together by slender Wires. These bits of Wood were covered on every Square with Paper pasted on them, and on these Papers were written all the Words of their Language, in their several Moods, Tenses, and Declensions, but without any Order. The Professor then desired me to observe, for he was going to set his Engine at Work.

I have commented in another thread about the Combinatorics satirized by Swift, in the last paragraph above, on filtering meaning from randomly generated strings of words, as it relates to Lull and later to Babbage and then “The Library of Babel” by Borges and the mining of ideocosm by Wolfram et al.

Posted by: Jonathan Vos Post on July 16, 2008 7:17 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

I had a question I wanted to ask John Baez. There’s no obvious place to ask it so I thought I’d ask it here.

I read “Fearless Symmetry, Exposing Hidden Patterns in Numbers” by Avner Ash and Robert Gross. It was from their book, that I was introduced to Galois theory. In their book, they explain Galois theory as a group of permutations where if you put in one number that is the root of a polynomial equation, you get back another root of the polynomial equation.

However, in John Baez’s recent This Week’s Finds, he says, “The basic principle of Galois theory says that covering spaces of a connected space are classified by subgroups of its fundamental group”.

How does this relate to the description of Galois theory in the book “Fearless Symmetry” and Avner Ash and Robert Gross?

Jeffery Winkler

http://www.geocities.com/jefferywinkler

Posted by: Jeffery Winkler on July 18, 2008 8:05 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

I think that John’s being a little facile, but not without good reason. There’s some really deep stuff going on here.

Basically, the idea is that a covering space comes with some really useful symmetry transformations: those that shuffle around the “copies” of the base space, but doesn’t change the shadow of any point. It turns out that this group of so-called “deck transformations” is (isomorphic to) a subgroup of the fundamental group of the base space, setting up a correspondence.

On the field theory end, when we extend a field (like the rational numbers) by adjoining the root of some polynomial, we get a larger field. Then there are automorphisms of this larger field which fix all the elements of the original field (sound sort of familiar?). The group of such transformations is called the “Galois group” of the extension. Subgroups of this group correspond to extension fields intermediate between the larger and smaller fields.

These two correspondences share certain formal properties which are very nicely stated in category-theory terms. We call such a situation a “Galois correspondence”.

But if you’re really paying attention, like Grothendieck was, you’ll realize that there’s something really deep going on. When you look with your algebraic geometry glasses (and you have to squint a bit yet) you see that an extension field is a covering space, in a sense. What exactly that means is where I start to lose track, but we can’t all be experts on everything.

Posted by: John Armstrong on July 18, 2008 10:29 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Field extensions are dual to the notion of covering spaces. We get the first clue to this from the fact that there is a surjection from the covering space to the base space, but an injection from the subfield to extension fields.

The next step is to see that (at least in some cases) we get an actual field of rational functions on the covering space, with a subfield consisting of those functions which are well-defined on the base space. (That is, have the same value on the inverse images of each point in the base space.) Obviously, the deck transformations on the space induce Galois transformations on the field. And intermediate covering spaces correspond to intermediate fields and to subgroups of the Galois group.

Posted by: Tim Silverman on July 18, 2008 10:52 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Jeffrey wrote:

I had a question I wanted to ask John Baez. There’s no obvious place to ask it so I thought I’d ask it here.

Okay. The blog entry on fundamental groups in number theory would be most the appropriate one, since it deals with precisely this issue… but it’s no big deal.

(And I don’t actually recommend reading that entry to understand this issue, since it assumes you’re already comfortable with the relation between Galois groups and covering spaces.)

I read “Fearless Symmetry, Exposing Hidden Patterns in Numbers” by Avner Ash and Robert Gross.

That’s a fun book!

It was from their book, that I was introduced to Galois theory. In their book, they explain Galois theory as a group of permutations where if you put in one number that is the root of a polynomial equation, you get back another root of the polynomial equation.

Right, this is the usual way people start explaining Galois theory. A bit more generally, Galois theory assumes you have a little field $k$ sitting in a big field $K$ ; the Galois group is then the group of symmetries of $K$ that are the identity on $k$ . For example, $k$ could be the rational numbers and $K$ could be the larger field formed by throwing in all the roots of some polynomial equation. Then the Galois group as I just explained it reduces to what you just described.

However, in John Baez’s recent This Week’s Finds, he says, “The basic principle of Galois theory says that covering spaces of a connected space are classified by subgroups of its fundamental group”.

How does this relate to the description of Galois theory in the book “Fearless Symmetry” and Avner Ash and Robert Gross?

John Armstrong and Tim Silverman have already given nice explanations, but let me take a crack at it too.

Very roughly, the idea is that we can think of any field as the field of functions on some space. If we have a little field $k$ sitting in a big field $K$ , this corresponds to a big space $S$ that’s a covering space of a little space $s$ . The Galois group then corresponds to the group of ‘deck transformations’ of this covering space: that is, transformations that permute sheets of the covering space.

And, just as spaces covered by $S$ but covering $s$ are classified by subgroups of the group of deck transformations, fields contained in $K$ but containing $k$ are classified by subgroups of the Galois group! This is often called the ‘Galois correspondence’ — but it’s the same as what I was calling the ‘basic principle of Galois theory’.

There are technical subtleties here that I’m omitting for simplicity, but getting a vivid geometrical picture of what’s going on will make it a lot easier to fight your way through those subtleties, if you ever care to do so.

What if you just want to learn a little bit more about this stuff?

Being quite biased, I urge you to start with the quick introduction to Galois groups in week201. See how the Lorentz group is an example of a Galois group! Learn the general concept of a Galois correspondence! And learn a precise statement of the Fundamental Theorem of Galois Theory!

Then, learn more about the analogy between the inclusion of a little field in a big one and the covering of a little space by a big one in week205. See how this is part of a big analogy between geometry and number theory! Learn how in this analogy, primes correspond to points! And learn about some of the subtleties I haven’t mentioned yet. For example, it’s not really fields so much as commutative rings that you should think of as corresponding to spaces, and the inclusion of a little commutative ring in a big one is really more like a branched covering space.

You’ve probably run into ‘branch points’ in complex analysis, and branched covering spaces like the Riemann surface for the square root function. Taking subtleties like this into account makes the analogy between number theory and complex geometry very precise! For more, try week218. It leads up to an analogy chart like this:

NUMBER THEORY                 COMPLEX GEOMETRY


Integers                      Polynomial functions on the complex plane
Rational numbers              Rational functions on the complex plane
Prime numbers                 Points in the complex plane
Integers mod p^n              (n-1)st-order Taylor series
p-adic integers               Taylor series
p-adic numbers                Laurent series
Adeles for the rationals      Adeles for the rational functions
Fields                        One-point spaces
Homomorphisms to fields       Maps from one-point spaces
Algebraic number fields       Branched covering spaces of the complex plane

I should emphasize that this analogy is not some new idea of mine: it’s completely taken for granted in modern number theory! But it’s incredibly cool, so everyone should learn about it.

Posted by: John Baez on July 19, 2008 5:00 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

The fact that Span gives bialgebras and Cospan gives separable algebras was what made me feel the paper was worth writing.

It would be interesting if someone could come up with a precise sense in which these PROPs are dual. Of course for a category E with pushouts and pullbacks we have $Cospan(E)=Span(E^{op})$ (at least as categories, for the bicategories you need to reverse the direction of the 2-cells on one side). That equation looks like something is dual, but as PROPs you don’t really have access to E. Is there some sense in which they really are dual?

Posted by: Steve Lack on July 25, 2008 9:02 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

It’s a great paper, Steve! Clearly you deserve a lot of coffee, even if you didn’t claim your reward in time.

Is there some sense in which they really are dual?

I don’t know the answer to that question, but there are others that might be easier.

First, the group algebra of a finite abelian group is both a bicommutative bialgebra and commutative separable Frobenius algebra, with the same multiplication but different comultiplications. There could be other compatibility relations that hold — I forget.

What’s going on here? Hopf algebraists have some idea about this stuff, involving the concept of an ‘integral’ for a Hopf algebra. Kuperberg’s work on involutory Hopf algebras and 3-manifold invariants should shed some light on this. But what’s the relevant PROP, and why do finite abelian groups give algebras for this PROP? Is some sort of weird ‘blending’ of spans and cospans involved?

Similarly, the group algebra of a finite nonabelian group is both a Hopf algebra and a separable noncommutative Frobenius algebra. Again, there’s an ‘integral’ involved… but what’s the story in terms of PROPs?

And another question: what happens if we take some other nice categories $E$ and work out $Span(E)$ and $Cospan(E)$ ? Do we sometimes get interestingly related PROPs? Are there interesting gadgets that are algebras of both these PROPs?

Posted by: John Baez on July 25, 2008 2:57 PM | Permalink | Reply to this

Re: Theorems Into Coffee IV

Steve,

In section 5 (Example) of your above mentioned paper subsection 5.3. you write: “A morphism in $F \otimes F^{op}$ from $m$ to $n$ consists of morphisms: $p \rightarrow m$ and $p \rightarrow n$ in $F$;”

should $m$ as an element of $F \otimes F^{op}$ be viewed as element of $F$ by some natural embedding also?

subsection 5.9:
What is the tensor product on $D \otimes P$ ? A disjoint union?
What do you mean with the term “order preserving on fibres of $\psi’$” ?
(where $\psi’$ is an order preserving map, what is the fibre of a map?)

May be this question can be answered by explaining why John claims that $D \otimes P$ is the same as P with morphisms being functions equipped with a linear ordering? Can one make this a little bit more precise?

Thanks in advance for the answer!

Posted by: george on August 3, 2008 6:33 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

John, thanks for your comments. Not sure if the things you discuss are easier, but certainly they are interesting.

George, you write

In section 5 (Example) of your above mentioned paper subsection 5.3. you write: “A morphism in $F \otimes F^{op}$ from $m$ to $n$ consists of morphisms: $p \rightarrow m$ and $p \rightarrow n$ in $F$ ;”

should $m$ as an element of $F \otimes F^{op}$ be viewed as element of $F$ by some natural embedding also?

All of these categories are PROPs, which means in particular that for all of them the objects are just the natural numbers. But it’s also true that $F$ can be embedded in $F\otimes F^{op}$ . This corresponds to the case where the arrow $p\to m$ is an identity. It is also analogous to the fact that for a tensor product $R\otimes S$ of rings, we can regard $R$ as sitting inside $R\otimes S$ .

subsection 5.9: What is the tensor product on $D \otimes P$ ? A disjoint union?

Yes.

What do you mean with the term “order preserving on fibres of $\psi$ ” ? (where $\psi$ is an order preserving map, what is the fibre of a map?)

A fibre of a map $f:X\to Y$ is a set of the form $\{x\in X\mid f(x)=y\}$ for some $y\in Y$ .

“Order preserving on the fibres of $\psi$ ” means that it respects the relation $x\le y$ if $\psi x=\psi y$ , but need not respect $x\le y$ for general $x$ and $y$ in the domain of $\psi$ .

May be this question can be answered by explaining why John claims that $D \otimes P$ is the same as P with morphisms being functions equipped with a linear ordering? Can one make this a little bit more precise?

A morphism in $D\otimes P$ from $m$ to $n$ consists of a permutation $\pi$ of $m$ and an order-preserving map $f:m\to n$ . This provides us with a function $m\to n$ , namely the composite $g=f\pi$ . This process is surjective but not injective. How can we recover $\pi$ from $g$ ? Think of $\pi$ as a linear ordering of $m$ . We put $i$ before $j$ if $g i \lt g j$ , but if $g i=g j$ we need some more information to know which of $i$ and $j$ comes first. This is what the order on the fibres does.

Posted by: Steve Lack on August 12, 2008 6:53 AM | Permalink | Reply to this

Re: Theorems Into Coffee IV

$MathML-enabled post (click for more details).$

Here’s a tiny bit of progress on trying to understand the relation between Hopf algebras and Frobenius algebras, and set the fact that a group algebra is often both into its PROPer context.

Lars Kadison and A. A. Stolin, An approach to Hopf algebras via Frobenius coordinates.

These authors work with algebras over commutative rings, but I will attempt to water down their results and work only with algebras over a field $k$ . The idea is to generalize the fact that the algebra of $k$ -valued functions on a finite group $G$ is equipped with an ‘integral’ sending any function $f : G \to k$ to $\sum_{g \in G} f(g)$ . This integral is invariant under translations, and it can be used to make into a Frobenius algebra.

To do this, they recall a notion due to Bodo Pareigis:

Bodo Pareigis, When Hopf algebras are Frobenius algebras, Jour. Algebra 18 (1971), 588-596.

Namely: an FH-algebra is a bialgebra $H$ with a linear functional

$\int : H \to k$

such that the bilinear form

$g(a,b) = \int(a b)$

is nondegenerate and $\int$ is a ‘right integral’ for $H$ . Here a linear map

$\int : H \to k$

is said to be a right integral for the bialgebra $H$ if

$H \stackrel{\Delta}{\to} H \otimes H \stackrel{\int \otimes 1}{\to} H$

is equal to

$H \stackrel{\int}{\to} k \stackrel{i}{\to} H$

(This is a clever way of generalizing the fact that the usual integral for function on $G$ is invariant under right translations.)

Clearly the nondegenerate bilinear form $g$ makes any FH-algebra into a Frobenius algebra; Pareigis also shows that any FH-algebra has an antipode making it into a Hopf algebra! It would be nice to see if we can prove this ‘purely diagrammatically’, so it works inside any symmetric monoidal category.

Kadison and Stolin also show some other tantalizing things:

Theorem: $H$ is an FH-algebra if and only if $H^*$ is an FH-algebra.

(This statement is a bit unclear, since it makes it sound like ‘being an FH-algebra’ is a property of a bialgebra rather than extra structure. The authors also define ‘Frobenius algebra’ in a funny way that makes it sound like being Frobenius is merely an extra property… which it’s not. But I hope all this can be cleaned up; presumably above they mean the usual dualization of Hopf algebras can be extended to a functor sending FH-algebras to FH-algebras.)

Theorem: $H$ is an FH-algebra if and only if it is a Frobenius algebra and a Hopf algebra.

(Again, this way of stating it is not very clear, but presumably they mean something interesting.)

Posted by: John Baez on August 17, 2008 2:46 AM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

July 12, 2008