This Week's Finds in Mathematical Physics (Week 265)

May 26, 2008

This Week’s Finds in Mathematical Physics (Week 265)

Posted by John Baez

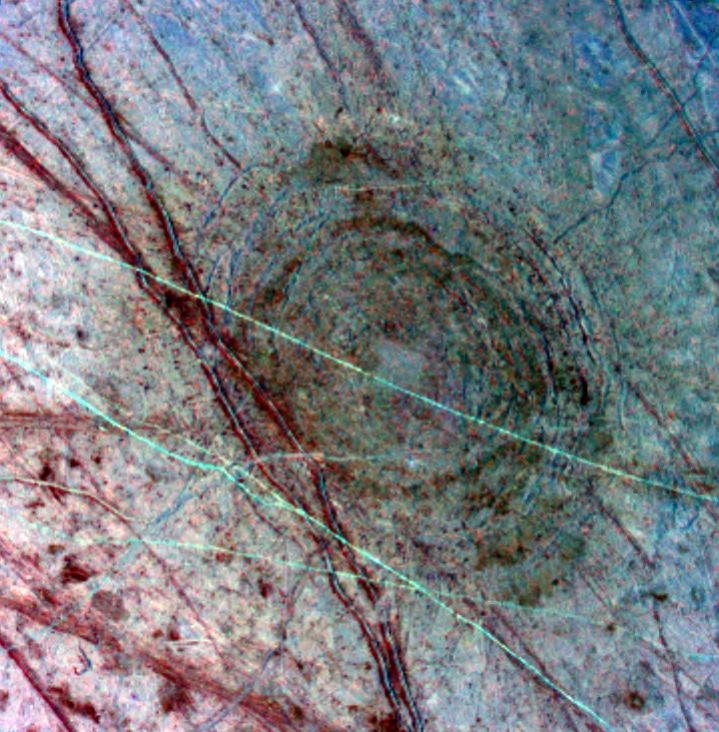
$MathML-enabled post (click for more details).$

In week265 of This Week’s Finds, see Europa, the icy moon of Jupiter:

Then read about the Pythagorean pentagram, Bill Schmitt’s work on Hopf algebras in combinatorics, the magnum opus of Aguiar and Mahajan, and quaternionic analysis!

$MathML-enabled post (click for more details).$

Here’s a nice picture of the cracked icy surface of Europa:

The red stuff in this false color image could be ice containing more salts — maybe magnesium sulfate — or maybe ice mixed with sulfuric acid.

I may give up listing questions raised by writing This Week’s Finds, since nobody seems to answer them! Still:

What’s the red stuff in the picture above? Nobody knows, apparently, but why do folks seem to feel sure it involves sulfur? What’s up with all this sulfur? Why is there so much sulfur on Io? Is it related?
People seem to say the ‘true polar wander’ in Europa is evidence for an ice sheet floating on an ocean, but there’s also true polar wander on Mars. What’s up? Is it just the enormous amount of polar wander on Europa that suggests a floating ice sheet?
What textual evidence is there concerning the Pythagoreans? The silly stories of Diogenes Laertius surely can’t be trusted too far. There’s a bit in Aristotle’s Physics. But this business about Pythagoreans and pentagrams — while it’s discussed quite extensively on Wikipedia, there are no references, and a lot concerns “medieval neoPythagoreans”. I want to know what we really know about the Greek Pythagoreans, and how we know it.
What’s going on with the big table of variant binomial coefficients on the first page of Aguiar’s paper Braids, q-binomials and quantum groups? It looks like one of those mystical Rosetta stones linking diverse subjects… I love those.
Precisely how are Aguiar and Mahajan’s $n$ -monoidal categories related to the $n$ -fold monoidal categories of Fiederowicz, Forcey and others? Do they still give $n$ -fold loop spaces? How do the combinatorial examples of $n$ -monoidal categories work?
How are Aguiar and Mahajan’s Fock space constructions related to the categorified and $q$ -deformed Fock spaces that I like? How is their work on $A_n$ Coxeter groups related to the groupoidified Hecke algebras that Todd, Jim and I are studying? I note that they mention positive braids.
Why do Frenkel and Libine say the quaternionic analogue of the Cauchy–Riemann equations is like Maxwell’s equations, when it so visibly resembles the Dirac equations?

Posted at May 26, 2008 7:02 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1694

49 Comments & 0 Trackbacks

Re: This Week’s Finds in Mathematical Physics (Week 265)

You say each pentagram is 1/phi times as big as the one before. Do you mean that each pentagram is 1/phi^2 times as big, or that it’s lines are 1/phi times as big, instead of the area being 1/phi times as big?

Posted by: anon on May 26, 2008 3:40 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

I’m measuring sizes by length, not area. I’m saying that each red line segment here is $1/\Phi$ as long as the bigger one below it:

By the way, a lot of people use $\Phi$ to mean $1.618...$ and $\phi$ to mean $1/\Phi = 0.618...$ , so it’s good to be careful about “Phi” versus “phi”.

Posted by: John Baez on May 26, 2008 6:45 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

I belatedly posted a list of questions I’d love help on for this Week’s Finds. I hope people will take a crack at some of these…

Posted by: John Baez on May 26, 2008 7:38 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

On Pythagoras and Pythagoreanism, you could do worse than follow the references in Wikipedia.

The absolute classic investigation of what is really known is Walter Burkert’s Lore and Science in Ancient Pythagoreanism. This is a very dense and scholarly discussion of the sources and related material (archaeological, mythographical), which demolishes much of the traditional picture of Pythagoras—classical scholarship at its best. Burkert is a towering figure in this field, and this book has massively influenced all serious later studies of Pythagoras. It’s very dense, and some readers will think it very slow going, but I found it absolutely exhilarating.

For a nice short review of the present situation in Pythagorean studies, there’s this web article by M F Burnyeat, with pointers to some other books.

There are many books on the presocratics in general, starting with the extensive collection of fragments and testimonials in Diels, Krantz Fragments of the Presocratics, as well as particular studies. Some of them discuss Pythagoras directly, or as part of the background. I can recommend more books if you want, but I’m not sure what I can add to a search through the library catalogues.

Posted by: Tim Silverman on May 26, 2008 9:52 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Thanks a zillion! I’ll try to grab Burkert’s Lore and Science in Ancient Pythagoreanism when I go by the library tomorrow. I think my wife has Fragments of the Presocratics — doesn’t any well-equipped classicist?

But you’ve already done a lot of study of this stuff. What stands out in your mind as a big thing you’ve learned?

(I already knew Pythagoras gets a fairly low score in the people who may or may not actually exist game.)

Posted by: John Baez on May 26, 2008 10:14 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

What stands out in my mind is how much less I know than when I started! Once upon a time, things seemed so clear …

The other things that stand out (now that you’ve put me on the spot) are mainly meta-things: how long it took the Greeks to move over from a mythological way of thinking to a scientific way of thinking, and how spectacular the change was, once it really got going. How hard historians try to interpret the thought of the past in terms of their own interests, and how much better this works when there is some sort of natural sympathy between their outlook and that of their subjects; otherwise, we have philosphically inclined historians (or historically inclined philosophers) trying to interpret science as a branch of philosophy; or mathematical historians trying to interpret mythology as mathematics. And how such a surprisingly large proportion of people who study mythology fall into just two classes: either they understand it, but they’re a bit nuts; or they’re sane, but they don’t really get it. Not all of them, but an amazingly large number.

I feel I should say something about actual mathematical content, seeing as that’s the subject of this blog. But it’s all a bit hazy. The importance of harmonics in stimulating early interest in number theory stands out; so does the importance of the split between the akousmatikoi and the mathematikoi—those who passed on traditional sayings and those engaged in some kind of theorising, perhaps—even though the details are a bit obscure.

It’s still very unclear to me what the relationship was at an early stage between geometry and number theory; or where geometry came from; or what was the relationship between Pythagorean mathematics, or mathematicians, and other possible mathematicians (did the Pythagoreans borrow from others? influence others? both? were they more or less sophisticated mathematicians than other presocratic philosophers? It’s clear—or as clear as anything in this murky area can be— that their beginnings were far from auspicious, but how much did Pythagorean mathematics develop? and how? and why? And what was going on in the sixth century, before Pythagoras came on the scene?) As I said, all this is much less clear to me now than it once was. In a sense, it doesn’t matter much—it’s all part of the prehistory of mathematics, more than its real history—but it’s all very tantalising, precisely because it is so tempting to speculate about the true form of those shapes dimly seen in the mist. It’s the same sort of tantalising glimpses that made me fascinated by ancient Central Asian history, so dimly seen by both the Greek writers looking to their uttermost east and the Chinese writers looking to their uttermost west.

So, as usual, I am of very little help at all…

Posted by: Tim Silverman on May 27, 2008 11:15 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Actually your comments are very helpful, even if they’re mainly descriptions of things you (along with the rest of us, I suppose) don’t understand. It’s indeed fascinating how mathematics, supposedly so precise, has such poorly understood origins, so mixed with mysticism.

… how long it took the Greeks to move over from a mythological way of thinking to a scientific way of thinking, and how spectacular the change was…

I’m lucky that my wife studies such things, and has friends who do too. Right now she’s writing a book on divination in China and Greece. Without her, I probably wouldn’t know about Geoffrey Lloyd’s works on the history of science. If you haven’t read them, you might especially like Magic, Reason and Experience: Studies in the Origins and Development of Greek Science — but also Adversaries and Authorities: Investigations into Ancient Greek and Chinese Science and The Ambitions of Curiosity: Understanding the World in Ancient Greece and China.

Today I got the book you recommend, and a few others too!

Posted by: John Baez on May 29, 2008 3:59 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Indeed, I have a dog-eared copy of Magic, Reason and Experience on my shelves, which has been in my possession for many years. I haven’t re-read it for a while; perhaps I should. I also have Science, Folklore and Ideology, and recently found and devoured Polarity and Analogy (his first, I think—it had the definite feel of a young man’s book, more focused and less discursive than his later ones.) In fact, I attended one of Geoffrey Lloyd’s lectures when I was at university, although all I can remember of it now is what a flamboyant figure he cut among the otherwise rather tweedy dons, with his colourful clothes—a bright silken kerchief about his neck (or that is how I remember it)—and his deep, rolling and melodious voice (though perhaps I am imagining things here); his tremendous, very youthful-seeming, enthusiasm for his subject, and his great delight at the thought of the young minds assembled before him about to embark on this great intellectual adventure.

I haven’t got the last couple of books you mentioned, though, and I ought to, because I know almost nothing about Chinese science or mathematics, and need to know more; and about Indian science and mathematics, too. In fact, this is particularly true because one of the most intriguing things to me about the period of early Greek philosophy is the many parallels with contemporaneous developments in India (as well as the differences). What is more fascinating still is that if a lot of this stuff was going on at the same time, there is always the possibility that some of the similarities were not independent parallels but indirect influences. We know for sure that cultural influences did spread back and forth among the cultures of the Mediterranean, Middle East, Persia and India (as well as even Central Asia and China), but how, when, where, why and, largely, what is hopelessly murky, leaving that awful tantalising situation where it is so much easier to speculate than to know. Heigh ho!

But that’s enough rambling for now, I think. So much to learn, and so little time to learn it!

Posted by: Tim Silverman on May 29, 2008 9:20 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Tim wrote:

In fact, I attended one of Geoffrey Lloyd’s lectures when I was at university, although all I can remember of it now is what a flamboyant figure he cut among the otherwise rather tweedy dons, with his colourful clothes—a bright silken kerchief about his neck (or that is how I remember it)—and his deep, rolling and melodious voice (though perhaps I am imagining things here); his tremendous, very youthful-seeming, enthusiasm for his subject…

He’s older now, but that description still rings true. I last saw him in Beijing a few summers ago, along with his collaborator Nathan Sivin, a famous sinologist who played a key role in helping Lloyd branch out from Greece to China. (And since we’re talking about clothes, check out this.)

What is more fascinating still is that if a lot of this stuff was going on at the same time, there is always the possibility that some of the similarities were not independent parallels but indirect influences.

Past a certain point, these influences are quite well-attested, but when you get back to the Warring States period (475-221 BC, when a lot of cool intellectual stuff was happening in China and also Greece) there is no solid evidence of any information transfer between China and Greece — just ghostly possibilities, like Zoroastrian physicians travelling along some early version of the Silk road. There’s not even any solid evidence of Indian influence on China until considerably later.

So, while some people enjoy speculating about these things, my wife (Lisa Raphals, who focuses on the Warring States period) prefers to compare classical China and Greece as examples of what civilizations can do, without worrying much about the possibility of causal connections.

Much later, of course, we get incredibly cool stuff like Graeco-Buddhist art in Khotan, and that bronze Buddha found in a Viking hoarde on an island off Sweden. Oh, it would be so fun to have a time machine…

Posted by: John Baez on May 29, 2008 10:07 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

On parallels versus influences: I’m not so concerned about China, but the closer you get to Greece, the more possibility there is of actual cultural transfer. It worries me, when I’m thinking about parallel developments, that, while I am imagining that similar ideas are arising because of, say, comparable political or economic situations, the real reason is, say, the spread of a religious cult. These two types of similarity (homology and analogy in biological terms) are very different, and require different sorts of explanation. I don’t want to mix them up, but it seems it’s unavoidable! But then I might end up making the same sort of mistake as those mildly crackpotty websites about a supposed historical basis for mythical Great Flood stories, which cite Flood stories from Greece, Egypt, Ancient Israel, the Hittites and Babylonia as though they were independent sources.

On Graeco-Buddhist art, wow, yes. Not only have I blinked in surprise at Gandharan artefacts on the Silk Road, but once spent an eye-opening afternoon in the British museum watching the influence of Greek sculpture spread east, through cultural influence in Asia Minor, to Greek architects at Persepolis, to Alexander’s conquests in Bactria, and then, carried by Buddhism, through Central Asia and India into Java and ultimately to Indo-China, many centuries after it started. It was absolutely amazing to see the ‘before’ and ‘after’ versions of local sculpture.

Not just a time machine, but a time machine and several lifetimes to use it in. That’s what we need.

Posted by: Tim Silverman on May 29, 2008 11:31 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

On the other hand, consider the truncation of Greek influence after the fall of Rome
if not earlier. I used to teach projective geometry illustrated with the development of perspective during the Renaissance, as if such accurate rendering were new then. I was totally ignorant of the riches of Greek renderings cf.walls or floors in Pompeii.

Posted by: jim stasheff on June 2, 2008 1:39 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Thanks for hinting to these books! Conc. greek philosophy and math. , here a book about “platonic number theory”. The author’s talks „Die Bedeutung der Mathematik in der Philosophie des antiken Platonismus“ , „Phantasia als Organon. Anschauung und Phantasie in der platonischen Wissenschaftstheorie am Beispiel der Geometrie“ touch interesting issues too.

Posted by: Thomas Riepe on June 1, 2008 2:08 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

My talk on the number 5 featured some not–too-serious musings on how the Pythagoreans may have invented the dodecahedron after seeing pyrite crystals in Sicily, and been fascinated by the pentagram because of how it contains a built-in proof of the irrationality of the golden ratio. So, it’s interesting to read this passage in Burnyeat’s review:

Theodorus of Cyrene was the first to prove, case by individual case, the irrationality of the square roots of the prime numbers from 3 to 17, while his pupil Theaetetus of Athens early in the fourth century produced the first general theory of irrationality and the first general account of the construction of the five regular solids (cube, tetrahedron, octahedron, dodecahedron, icosahedron).

This is powerful, mainstream mathematics, a far cry from the numerology of marriage. Yet not one of the names just mentioned is that of a Pythagorean, not one comes from southern Italy. Still, there is one name that prompts a question. Why would Theodorus begin his proofs with the irrationality of $\sqrt{3}$ if not because the irrationality of $\sqrt{2}$ was already known? Who, then, discovered this, the first and most elementary case of irrationality?

The simple answer is that no one knows. Numerous books (Penrose’s included) will tell you that the discovery was felt by the Pythagoreans as a great shock, for it threatened their attempt to explain the world in terms of whole-number ratios on the model of the musical concords. Ancient testimony to this claim is non-existent. All there is is a late story, found in the Neoplatonist Iamblichus’ Life of Pythagoras (fourth century AD), that divinity drowned at sea the Pythagorean who made the discovery public, in breach of the ban (itself of dubious historicity) on divulging to outsiders any detail of what took place within the school.

Enter now the first Pythagorean to be credited with a significant mathematical discovery, Hippasus of Metapontum in southern Italy. Date uncertain, the best estimate being that he was active around 450 BC in the generation before Theodorus. Now, according to the same late compilation by Iamblichus, Hippasus was the first to show how to construct a dodecahedron and to publish his discovery – in punishment for which he was drowned at sea. For all that sea travel in antiquity was a hazardous undertaking, with shipwreck a common occurrence, some scholars unite the two drowning stories and suppose that Hippasus’ punishment was for revealing both the fact of irrationality and the construction of the dodecahedron; it has even been suggested that he discovered irrationality in the course of working on the dodecahedron.

Posted by: John Baez on May 29, 2008 6:10 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

“The Suan shu shu is the earliest known extensive Chinese writing on mathematics.” (Found on the Needham site.)

Posted by: Thomas Riepe on May 30, 2008 8:19 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Here a related review:
http://online.wsj.com:80/article/SB121099042973500689.html

Posted by: Thomas Riepe on May 31, 2008 11:37 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

The Pythagoreans were object of an antique equivalent of an investigative reporter, Empedocles. They excluded him and interdicted any future participation of writers, but Empedocles had already published.

Posted by: Thomas Riepe on June 3, 2008 8:41 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Frenkel and Libine don’t say that the quaternionic analogue of the Cauchy-Riemann equations is like Maxwell’s equations; in fact, they identify it as the massless Dirac equation in the introduction on page 6. Rather, Maxwell’s equations show up as the quaternionic analogue of the (second-order) Cauchy formula:

(1)

f'(w) = \frac{1}{2\pi i} \int \frac{f(z)\,dz}{(z - w)^2}

Well, almost. For functions for which $\text{Mx}\,F\,\text{:=}\,\nabla F \nabla - \square F^+ \equiv 0$ (which we are supposed to interpret as the analogues of constant functions, for which $f' \equiv 0$ ), this equation can be seen to be a formulation of Maxwell’s equations in a vacuum. I wonder if there’s any fruitful interpretation of the general Maxwell’s Equations in this setting.

Posted by: Evan Jenkins on May 26, 2008 10:37 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

I wonder if there’s any fruitful interpretation of the general Maxwell’s Equations in this setting.

Well, as I’ve remarked in previous posts , geometric algebra does precisely this… if I understand you correctly. As per usual, one combines the charge density and charge current into a four-vector $J$ , and the electric and magnetic fields into a bivector $F$ . ‘Old-school’ differential-form calculus tells us that Maxwell’s equations are

(1)

dF = 0 \quad \text{and} \quad d * F = J,

but geometric algebra (if you insist, ‘quaternionic analysis’, but so far I have to admit to preferring the simple intuitive geometric algebra formulation) goes one better. It combines both these equations into one equation:

(2)

\nabla F = J.

The geometric derivative of the force bivector is the source bivector.

Posted by: Bruce Bartlett on May 27, 2008 12:13 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Woops, that was a slip-up on my behalf… $F$ is of course the electromagnetic field, not the “force”. The force comes from the Lorentz force law… or alternatively from the geodesic equation. In geometric algebra, the role of the Lorentz force law is played by the rotor equation:

(1)

\dot{R} = \frac{1}{2} F R

Here is a cool overview. Warning: if one gets into geometric algebra, sooner or later one starts to believe that the mathematical world has been suffering from a thought virus for over a century. Sometimes I am tempted by this philosophy :-)

Posted by: Bruce Bartlett on May 27, 2008 12:41 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Speaking of thought viruses, what I find strange is when fans of geometric algebra act as if Clifford algebras a were secret weapon used only by a few rebels. It seems to me that ever since the work of Atiyah and Bott — not to mention Dirac — Clifford algebras have been central to ‘mainstream’ work on differential geometry and physics! If you read Michelson and Lawson’s Spin Geometry, you’ll see what I mean.

Posted by: John Baez on May 27, 2008 1:01 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

I have two things to say in response. Firstly, I would argue that Clifford algebras have not been as mainstream as they should have been - especially in those parts of theoretical physics not directly connected with string theory or quantum gravity. I regard Frenkel and Libine’s recent paper as direct proof of this!

Secondly, I would argue that Michelson and Lawson’s Spin Geometry, while in 99% of ways a fantastic text, actually has contributed in some sense to this situation, because it often eschews the geometric and intuitive for the algebraic and formal; witness “The Clifford algebra is the quotient of the tensor algebra by such and such an ideal”. That’s fine; I don’t argue with that. Formal definitions are okay as long as one is sure that the majority of readers will form the appropriate geometric conceptions. But history has shown that most mathematicians didn’t “flesh out” these formal definitions with the appropriate geometric intuition. Why are foundational papers on quaternionic analysis still being published over a century later?

Consider Figures 11 of Hestene’s review:

I find it a shocking indictment on the mathematical community that it was the physicists and computer scientists who produced these sorts of diagrams - which are in any case simply a return to Clifford’s original formulation. I know most mathematicians will say that privately they had this kind of intuition all along… but that’s the old depressing state of affairs, where the most important insights are the ones which never make it into mathematical books. And that left a gap in the market for the geometric algebra people.

Let me close by saying that I agree with you in the following sense: the geometric algebra group targeted their papers to “traditional” physicists, and not to mathematicians. In many ways we are innocent of their critique… but not completely.

Posted by: Bruce Bartlett on May 27, 2008 10:05 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Okay, I basically agree with your comments, which seem well-balanced and not too fanatical. I especially agree about the “the old depressing state of affairs, where the most important insights are the ones which never make it into mathematical books.” The problem, I guess, is that mathematicians learn to present definitions, theorems and proofs, but not ‘insights’. Those aren’t part of the structure of mathematics as currently formalized! Let’s hope that someday this seems like a primitive state of affairs.

Posted by: John Baez on May 29, 2008 5:00 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

To add a couple of comments from someone who uses mathematics in the context of engineering. There are a two problems with the geometric algebra approaches. The first is that almost everything they present is a recasting of something already known, which isn’t a completely convincing for saying that the approach is more insightful and hence powerful than conventional views. Secondly and more importantly, a lot of the things they present are the “neatest” cases where lots of things fall into place automatically without this fact ever being noted in the text. If you take one of their calculations and try and make some minor change to the basic problem and try to redo it there’s often something that crops up so the calculation bogs down in complications that happen not to manifest in the demonstrated calculation. I’d like to invest more time using (and hence studying) geometric algebra but I’d like to see lots more work available before I could state for sure it’s not the equivalent of the way some photographs make the handsome parts of a subject stand out and the problems like the beer gut become unnoticeable in the shadows that happen to fall. (To be clear, I’m emphatically not suggesting any deceptiveness, merely that only the best bits have been reported so far.)

Posted by: bane on May 30, 2008 10:50 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Hi bane, yes I understand where you’re coming from about how many of the advertised examples only work in the “neatest” cases; I’ve had that experience before as well. I suspect though most of the time it just needs more thought; one should be able to come up with an elegant geometric explanation for all the constructions.

Their main point is: Look guys, this Clifford algebra stuff is really simple and intuitive, why are you all doing it in such a roundabout and complicated way?

That’s why it resonates with me — it is very similar to the zeitgeist on this blog!

Posted by: Bruce Bartlett on June 4, 2008 1:38 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Bruce Bartlett wrote:

Formal definitions are okay as long as one is sure that the majority of readers will form the appropriate geometric conceptions.

As a dumb layman, I wish more mathematicians and physicists would be willing to state the (near) obvious. Even the very reader-friendly and illustration-packed Gravitation by Misner, Thorne and Wheeler gives us Killing’s equation:

$\xi_{\mu;\nu} + \xi_{\nu;\mu} = 0$

with no further comment. Now, I suppose you could argue that anyone who’s reached Chapter 25 of this book should be so immersed in tensor geometry that they can immediately see that what this means in English is the covariant derivative of $\xi$ in any direction u will be orthogonal to u, and will then realise that this is an infinitesimal version of an almost primary-school-level geometric fact about rigid motion … but still, I wish they had taken the effort to spell it out. Though I suppose this is a marginal example, given that the baseline exposition in MTW is already set to a very high level, I suspect that the mathematics and physics literature in general could probably increase its accessibility by a factor of 10 with an increase of maybe 25% in word length, just by pointing out things that the authors find obvious but readers might not.

Posted by: Greg Egan on May 31, 2008 4:42 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Greg wrote:

As a dumb layman, I wish more mathematicians and physicists would be willing to state the (near) obvious.

Let’s not forget how easy it is for professionals to manipulate formulas without knowing what they mean. I’ve spent many years taking the equations I learned in physics class and struggling to translate them into something resembling plain English. It can be a lot of work!

The most embarrassing example was when, after a few years of working on quantum gravity, I realized that I couldn’t say what Einstein’s equation meant. Nobody had ever told me!

Right now Jim Dolan and I are struggling to do something similar for wads of modern number theory, from elliptic curves and modular forms and $L$ -functions on up to the modularity theorem and the Langlands program. Trying to get a simple explanation of this stuff out of the books I’ve seen is like trying to pull teeth… from a chicken.

Anyway, what I’m saying is that mathematicians and physicists often fail to state the obvious because they’ve never thought about it.

Posted by: John Baez on May 31, 2008 6:54 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

So what proportion of the time are the experts ‘sitting’ on the answer of what’s really going on compared to not having thought it out? I suppose there is also a middle ground of tacit knowing.

It’ll be interesting to see reactions to your ‘getting to the bottom of Langlands’ program, something so many top people have thought about.

Posted by: David Corfield on June 2, 2008 8:08 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

David wrote:

So what proportion of the time are the experts ‘sitting’ on the answer of what’s really going on compared to not having thought it out?

It’s hard to find out politely by asking: “Are you ‘sitting’ on your insights, or don’t you actually have any?”

It’ll be interesting to see reactions to your ‘getting to the bottom of Langlands’ program, something so many top people have thought about.

We certainly haven’t ‘gotten to the bottom’ of the Langlands program yet — we’re just starting. There’s a lot of background material! We spent a couple years learning about class field theory, which is sort of the abelian special case of the Langlands game. Even that, I still want to understand better — but at least on good days I see how there’s a sense in which some of the key results of class field theory, like Artin reciprocity, are ‘visually plausible’ if you freely take for granted the analogy between number fields and Riemann surfaces.

(This is well-known to experts, mind you; we’re just catching up. However, even some fairly serious books on number theory make it sound like the use of cohomology in class field theory is a scary or bad thing — when it actually means class field theory makes conceptual and geometrical sense)

I haven’t gotten anywhere near seeing some sense in which the Langlands program is similarly ‘plausible’ — and the annoying thing is that I can’t even tell if it is to experts, or not!

Of course even plausible things can be darn hard to prove — but I’m not hoping to prove anything about the Langlands program, just enjoy it as a kind of appreciative spectator.

I think I need to learn a bit more before I even dare start pestering experts. When I asked Minhyong about this stuff, he started talking about perverse sheaves, and it’s taken me about a year to recover.

Posted by: John Baez on June 2, 2008 10:31 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

I suppose “Are you sitting on your insights…?” is a little brusque. But surely you could elicit the fact with a more subtle line of questioning.

What would be very annoying would be to expose the bottom line of a theory only to have the experts say “Yes, of course we knew that clearly all the time”. Pleasanter would be “We knew that but didn’t have the means to express it.” Pleasantest, “Now we have a powerful insight into the field, and how to extend it, etc.”.

But even in the former case, and even if they were speaking the truth, in a reasonable world you’d receive great credit for your exposition. Which brings us back to the old point of why there is insufficient credit for novel exposition, raised by all sorts of leading figures – Rota, Thurston,…

Those on the other side of the two cultures divide from us are planning a Tricks wiki to gather their expositary insights. If we ever get our wiki going, a page of slogan-like insights (those juicy, capitalised statements of TWF) linking to their exposition would be good.

Posted by: David Corfield on June 3, 2008 9:33 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

David wrote:

I suppose “Are you sitting on your insights…?” is a little brusque.

Yeah — I’d never actually say that, but sometimes I’m really tempted.

What would be very annoying would be to expose the bottom line of a theory only to have the experts say “Yes, of course we knew that clearly all the time”. Pleasanter would be “We knew that but didn’t have the means to express it.” Pleasantest, “Now we have a powerful insight into the field, and how to extend it, etc.”.

Since I do a lot of exposition that tries to ‘expose the bottom line’ of different subjects — why all these metaphors involving the rear end, David? — I have some sense of what tends to happen.

For starters, everyone is very happy when someone else’s bottom line is exposed. Why? Mainly because experts in subject $A$ are always wondering what expert in subject $B$ are really doing! So, they’re glad to get any sort of simplified exposition that cuts through the technicalities and explains the big ideas.

But, it’s harder to please experts in a subject when you’re explaining that same subject. There are lots of obvious reasons for this, which I needn’t list.

Things get the most interesting when you’re doing exposition that seeks to improve a subject while explaining it. There’s a lot to say about this, but I’ll just pass one on obvious tip.

If you take a subject and explain some idea in it by showing that it’s a special case of some more general (often category-theoretic) idea, people can become actively hostile. Especially if you say it’s just a special case. Never do that! The word ‘just’ suggests that you’re looking down on their subject with the bemused interest of someone watching an anthill — so they’ll fight back with phrases like ‘abstract nonsense’, ‘mere formalism’, etc.

Posted by: John Baez on June 3, 2008 6:47 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

David wrote:

I suppose “Are you sitting on your insights…?” is a little brusque.

Yeah — I’d never actually say that, but sometimes I’m really tempted.

What would be very annoying would be to expose the bottom line of a theory only to have the experts say “Yes, of course we knew that clearly all the time”. Pleasanter would be “We knew that but didn’t have the means to express it.” Pleasantest, “Now we have a powerful insight into the field, and how to extend it, etc.”.

But, it’s harder to please experts in a subject when you’re explaining that same subject. There are lots of obvious reasons for this, which I needn’t list.

Things get the most interesting when you’re doing exposition that seeks to improve a subject while explaining it. There’s a lot to say about this, but I’ll just pass one on obvious tip.

Posted by: John Baez on June 3, 2008 6:48 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

John asks

why all these metaphors involving the rear end, David?

Well, we are accusing certain people of being retentive about their ideas.

Posted by: David Corfield on June 4, 2008 8:53 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

‘mere formalism’ - how developed the reception of e.g. derived categories, stacks,… in algebraic geometry?

Posted by: Thomas Riepe on June 4, 2008 9:39 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Thomas wrote:

‘mere formalism’ - how developed the reception of e.g. derived categories, stacks,… in algebraic geometry?

I don’t know. Surely someone will write a biography of Grothendieck or history of Bourbaki that chronicles the reaction of algebraic geometers to wave after wave of increasing abstraction. I get the feeling that by the time Grothendieck reached topoi, most algebraic geometers were sort of tired.

By the way, it’s against the rules to write “how developed the reception?” in English: we have to say “How did the reception develop?”

Good: “The queen danced.”

Good: “The queen did dance” — but beware, this means something slightly different, which I’m not smart enough to explain.

Good: “How did the queen dance?”

Bad: “How danced the queen?”

German and English are similar enough that we both easily get mixed up when trying to use each other’s verb tenses!

Posted by: John Baez on June 5, 2008 9:49 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Perhaps a more fundamental question is whether or not the Cauchy-Riemann equations need to be extended to quaternions and octonions in order to be able to define meaningful differentiation.

We are all familiar with properties lost along the way going from reals to octonions, like multiplicative commutation and associativity. I have no problem leaving the Cauchy-Riemann equations as requirements for only complex regularity.

I have defined H and O differentiation using the limit on ratio of hypersurface to hypervolume as the volume approaches zero as done with the integral definitions for standard divergence, curl, etc. This can nicely be cast in a diffeomorphic form showing transformation properties in terms of the fundamental definition of differentiation. Before you dismiss it out of hand since anything resembling the Cauchy-Riemann equations are no where to be found, I suggest you try it with something like familiar spherical-polar forms expected from quaternions.

I have presented octonion representations of electrodynamic fields, work, forces, energy and momentum conservation, along with non-electrodynamic fields, forces etc, that come along for the ride, available in a PDF on my website. This was announced in a post on SPR. The only play I got was Uncle Al, asking what I have that metric gravitation does not have. Oddly enough, my attempts to answer were not posted, and no explanation was ever offered by the moderators. Hmmm.

The lack of feedback is something like the flip side of the above sidetrack on this thread. The disclosure was made, but those experts in a position to respond and critique are the ones sitting on it.

I would especially like to know John’s opinion on what I have presented. As I told him three years ago when I sent him earlier work, I value his knowledge on the subject. Still do.

www.octospace.com

Rick Lockyer

Posted by: Rick Lockyer on June 6, 2008 1:36 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

I would presume the function f represents potential functions, and hence the first order differentiation would produce fields, which by the stated extension of the Cauchy-Riemann equations would be zero valued. Am I missing something here?

I would suggest a better cover of electrodynamics is offered by octonions, since the magnetic and electric field components have distinctly different fundamental multiplication characteristics which are matched by 6 of the seven octonion components. This can’t be done with quaternions without also going up in tensor rank. Not necessary with octonions. By casting electrodynamics inside octonion algebra, there appears a separate but analogous field to the electric field, gravitation?

For more information, see my website:

www.octospace.com

Posted by: Rick Lockyer on June 3, 2008 4:30 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

In regard to the questions about versions of iterated monoidal categories: these have been defined a bunch of times, with the loose pattern of “more recent implies more lax.”

Joyal and Street define “tensor categories with a multiplication” in section 5 of Braided tensor categories. Interchange is an isomorphism.

Baez and Dolan’s k-tuply monoidal n-categories also have isomorphisms for the interchanges.

Batanin defines monoidal globular categories as special sequences of iterated monoidal categories, with increasing numbers of products. Structure maps are isomorphisms. There are also source and target maps to the category with one less product.

Fiedorowicz, Vogt et.al. define n-fold monoidal categories. Interchange is just a natural transformation but unit maps are identities, and the unit is common.

Forcey, Siehler and Sowers define n-fold monoidal categories with distinct units, and unit maps that are isomorphisms. Units respect each others’ products. We also consider examples with associators that are not isomorphisms.

Aguiar and Mahajan’s definition removes all trace of isomorphisms, except the associators.

I’m not sure whether the versions with distinct units and structure maps that are not isomorphims still have nerves that are loop spaces.

The examples in the book/paper by Aguiar and Mahajan are of pairs of products on species. I’d like to know how they relate to our combinatorial examples of 2-fold and n-fold monoidal categories. In our example categories the morphisms are ordering, so the axioms are inequalities that are always satisfied. There are examples based on sequences, and on Young diagrams and n-dimensional Young diagams.

Here are powerpoint slides that start by describing some of the basic examples using Young diagrams.

Here’s the paper
Operads in iterated monoidal categories.
Also available from

JHRS.
Here’s
even more fun–higher products for Young diagrams.

And finally here’s a

way to take your favorite 2-fold monoidal category and get a twisted version by composing the interchange with a natural transformation of the identity functor. We give an example using free Z-modules.

Posted by: Stefan Forcey on May 29, 2008 9:19 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Terry Bollinger has given me permission to post his email response to ‘week265’:

Apparently there exists a pretty good argument that five-pointed stars were of interest to ancient astronomical because over a long enough period of time, Venus pops up (morning and evening) in a repeating five-point pattern across the constellations. See Carl G. Liungman’s Dictionary of Symbols. The relevant online excerpt (expect… unique… ads) is here.

None of the other planets do this, apparently. I would assume it’s an orbital resonance of some sort, but I’ve not looked into it. It could just be an unusual coincidence.

Mercury could also trace pop-up patterns, I suppose. (Hmm, isn’t Mercury in a resonance with Venus? I wonder how that would multiply out visually from here…). However, even in ancient times it was never easy to see, and always against a bright sky. I’ve seen it twice, but only with some very careful locating.

Uranus is actually far easier to see with the naked eye. I still find it quite bizarre, and likely a reflection of some kind of enforced numeric orthodoxy – “seven moving heavenly bodies max, and off with your head literally if you disagree” – that it is not listed as one of the eight persistent moving objects in the heavens, given that it pokes by Mars, Saturn, and Jupiter every so often. It’s almost inconceivable that old timers who lived under a real sky with a visible Milky Way did not take notice of it now and then. It was just moving too slowly, perhaps?

Posted by: John Baez on May 30, 2008 9:57 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Terry wrote:

… over a long enough period of time, Venus pops up (morning and evening) in a repeating five-point pattern across the constellations.

I would assume it’s an orbital resonance of some sort, but I’ve not looked into it.

A quick scan suggests that this appearance of the number 5 arises from the fact that Venus goes around the Sun about 13 times every 8 Earth years.

(I can hear Fibonacci fans world-wide sitting up in their chairs.)

More precisely,

$Earth year / Venus year \approx 1.6256$

while

$13/8 = 1.625$

However, it seems to be controversial whether this is a real resonance.

I still find it quite bizarre, and likely a reflection of some kind of enforced numeric orthodoxy – “seven moving heavenly bodies max, and off with your head literally if you disagree” – that it is not listed as one of the eight persistent moving objects in the heavens…

On the other hand, we can excuse Hegel from the persistent accusation that his dissertation contains a ‘proof’ that there can be only 7 planets.

What’s so great about 7? Last night I read that certain Pythagoreans — whoever they were — venerated the number 7 because among the first ten it’s the only number that neither divides nor is divisible by any other. For this they called it ‘motherless’, or ‘Athena’.

(In case you’re wondering, the Greeks did not consider 1 a number.)

That’s interesting, but it only pushes back the question: what’s so great about the number 10? To understand this, you have to realize that, in an amusing parody of current-day superstring theorists, the early Pythagoreans were really into the number 10. The reason was their fondness for the tetractys:

The identified the rows 1, 2, 3, 4 with the point, interval, triangle and tetrahedron — along with lots of other things. This is sort of cute, since it foreshadows the idea of taking the nerve of a totally ordered set and getting a simplex.

Warning: numerology is dangerous. It should be left to trained mathematicians.

Posted by: John Baez on May 30, 2008 10:18 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

What’s so great about 7?

I like to think it’s actually about music theory. “Everyone” knows that doubling the frequency of a note raises the tone by an octave. The next most harmonious interval is multiplying by 3/2, which corresponds to a perfect fifth.

So keep multiplying by 3/2 and divide by 2 when you need to stay within the 1-2 interval. After 12 factors you get 531441/524288 = 1.0136, which is the closest approach to 1 for a very long time.

It makes sense, then, to chop the interval up into 12 roughly equal spaces (methods of choosing these 12 ratios that multiply to give 2 are called “temperaments”). And then 12 is a very special number indeed, as we see over and over in antiquity.

But what happens to our old friend the perfect fifth? How many of these little pieces add, er, multiply up to give 3/2? Seven!

Posted by: John Armstrong on May 31, 2008 2:05 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

John B. wrote:

What’s so great about 7?

John A. wrote:

I like to think it’s actually about music theory.

Interesting point! Thanks to Tim Silverman’s suggestions, I’ve been reading about Pythagoreanism. The historical record of who did what when is incredibly murky. The so-called Pythagorean tuning system definitely faces up to the circle of fifths and the resulting Pythagorean comma

$\frac{(3/2)^{12}}{2^{7}} = 531441/524288 \simeq 1.0136$

However, I haven’t bumped into any references to Greek texts that relate the circle of fifths to the magical properties of the number 7. They instead talk about how 7 is the only number between 1 and 10 that neither divides nor is divisible by any other.

Again, 1 was not a ‘number’ to the Pythagorean numerologists, and 2 only became regarded as such relatively late! The reason may be that Ancient Greek and Attic Greek have, in addition to the usual ‘singular’ and ‘plural’, a dual’ form. The dual was common in early Indo-European languages, but English has it only vestigially, e.g. in words like ‘both’ (as opposed to ‘all’).

So, instead of being considered numbers, 1 and 2 were regarded as the building blocks from which numbers were made. This is somehow related to a story about how even is to odd as female is to male: you add male to female and the male wins! (Don’t ask me about male plus male.) It’s also for some reason like this that $5 = 2 + 3$ symbolized ‘marriage’.

In short, while your idea is logically satisfying, it could be that the early Greek thoughts about the number 7 were tied to other ways of thinking that seem quite alien to us now.

To add to the confusion, I have no idea who first coined the term ‘Pythagorean tuning’ or ‘Pythagorean comma’. Later scholars loved to attribute everything to Pythagoras. But it seems that the so-called ‘Pythagorean tuning’ goes back to Babylonians texts circa 3500 BC! At least that’s what they say in Wikipedia… and they’re never wrong.

Maybe someone can track this down and report on it:

M. L. West, The Babylonian musical notation and the Hurrian melodic texts, Music & Letters, Vol. 75, no. 2. (May 1994), pp. 161-179.

Posted by: John Baez on June 3, 2008 7:24 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

John B. wrote:

So, instead of being considered numbers, 1 and 2 were regarded as the building blocks from which numbers were made.

By the way, if you think the early Greeks were idiots for taking so long to decide 2 was a number, even longer to consider 1 a number, and never getting around to 0…

… just think what future scholars will think when they see we first invented 2-categories, then the term ‘1-categories’ for categories, then the term ‘0-categories’ for sets, and only recently (-1)-categories and (-2)-categories (which sort of suggest our whole numbering system for $n$ -categories is screwed up).

Humans notice patterns when they’re already underway, and then need to ‘back up’ to see where these patterns started.

Posted by: John Baez on June 3, 2008 7:35 PM | Permalink | Reply to this

From Greece to Zeta function; Re: This Week’s Finds in Mathematical Physics (Week 265)

pi quick points.

(1) When I took Category Theory at UMass in 1973 and argued for a (-1)-category I was shot down.

(2) As to 1 and primes as “building blocks” in 4 levels of abstraction (Chris Caldwell argument):

The number one is far more special than a prime! It is the unit (the building block) of the positive integers, hence the only integer which merits its own existence axiom in Peano’s axioms. It is the only multiplicative identity (1.a = a.1 = a for all numbers a). It is the only perfect nth power for all positive integers n. It is the only positive integer with exactly one positive divisor. But it is not a prime. So why not? Below we give four answers, each more technical than its precursor.
Answer One: By definition of prime!
The definition is as follows.

An integer greater than one is called a prime number if its only positive divisors (factors) are one and itself.

Clearly one is left out, but this does not really address the question “why?”
Answer Two: Because of the purpose of primes.
The formal notion of primes was introduced by Euclid in his study of perfect numbers (in his “geometry” classic The Elements). Euclid needed to know when an integer n factored into a product of smaller integers (a nontrivially factorization), hence he was interested in those numbers which did not factor. Using the definition above he proved:

The Fundamental Theorem of Arithmetic
Every positive integer greater than one can be written uniquely as a product of primes, with the prime factors in the product written in order of nondecreasing size.

Here we find the most important use of primes: they are the unique building blocks of the multiplicative group of integers. In discussion of warfare you often hear the phrase “divide and conquer.” The same principle holds in mathematics. Many of the properties of an integer can be traced back to the properties of its prime divisors, allowing us to divide the problem (literally) into smaller problems. The number one is useless in this regard because a = 1.a = 1.1.a = … That is, divisibility by one fails to provide us any information about a.
Answer Three: Because one is a unit.
Don’t go feeling sorry for one, it is part of an important class of numbers call the units (or divisors of unity). These are the elements (numbers) which have a multiplicative inverse. For example, in the usual integers there are two units {1, -1}. If we expand our purview to include the Gaussian integers {a+bi | a, b are integers}, then we have four units {1, -1, i, -i}. In some number systems there are infinitely many units.

So indeed there was a time that many folks defined one to be a prime, but it is the importance of units in modern mathematics that causes us to be much more careful with the number one (and with primes).
Answer Four: By the Generalized Definition of Prime.
(See also the technical note in The prime Glossary’ definition).

There was a time that many folks defined one to be a prime, but it is the importance of units and primes in modern mathematics that causes us to be much more careful with the number one (and with primes). When we only consider the positive integers, the role of one as a unit is blurred with its role as an identity; however, as we look at other number rings (a technical term for systems in which we can add, subtract and multiply), we see that the class of units is of fundamental importance and they must be found before we can even define the notion of a prime. For example, here is how Borevich and Shafarevich define prime number in their classic text “Number Theory:”

An element p of the ring D, nonzero and not a unit, is called prime if it can not be decomposed into factors p=ab, neither of which is a unit in D.

Sometimes numbers with this property are called irreducible and then the name prime is reserved for those numbers which when they divide a product ab, must divide a or b (these classes are the same for the ordinary integers–but not always in more general systems). Nevertheless, the units are a necessary precursors to the primes, and one falls in the class of units, not primes.

See, for example, the section on factoring primes in A Brief Introduction to Adelic Algebraic Number Theory.
Another prime page by Chris K. Caldwell

(3) From “Music of the Primes” on how we got from the Greek conception to the Zeta function

Euler discovered there is an alternative formula or recipe for the zeta function which depends on knowing the prime numbers:
(1) calculate px for each prime number p
(2) take the reciprocal of all the numbers in (1)
(3) take 1 away from all the numbers in (2)
(4) take the reciprocal of all the numbers in step (3)
(5) multiply all the numbers in step (4) together

That the two recipes cook the same cake depends on the fact that all the numbers 1,2,3,4… can be written as prime numbers multiplied together.

For example the number 60 is 2x2x3x5.

Euler realised that every term in his infinite sum like 1/60 could be pulled apart using the property that 60 is built out of its prime building blocks. So he wrote:

1/60=(1/2)x(1/2)x(1/3)x(1/5)
= (1/22)x(1/3)x(1/5)

But if he did this to every term in his infinite sum he could pull all the calculations apart and write them as:

1+1/2+1/3+…+1/60+…=
(1+1/2+1/22+…)(1+1/3+1/32+…)(1+1/5+1/52+…)…(1+1/p+1/p2+…)…

where each bracket contains all the powers of a particular prime. So each fraction 1/N in the infinite sum is built by multiplying a fraction from each bracket. If p is one of the building blocks of the number N appearing A times then take the fraction 1/pA from the p-bracket. If p is not a building block then simply choose 1.

You can try this on the first 10 fractions of the harmonic series:

1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+1/10+…
=(1+1/2+1/4+1/8+…)(1+1/3+1/9+…)(1+1/5+…)(1+1/7+…)(1+1/11+…

To get one of the fractions in the harmonic series, you have to pick one term from each bracket and multiply them together to get your choice from the harmonic series. For example to get 1/10, you’ll choose 1/2 from the 2-bracket and 1/5 from the 5-bracket and 1 from every other bracket.

OK, that admittedly was quite a heavy burst of equations. What you should take away from this is Euler’s observation that the infinite sums in which he was interested have connections with the primes because by multiplying together all the primes in different combinations you can reconstruct Euler’s sums. It is somehow a very neat way to express in one infinite equation the Greeks’ observation that numbers are built out of primes. Euler’s expression, known today as Euler’s product, can be summed up as “Adding fractions=Multiplying reciprocals of primes”.

It was when he took the logarithm of the harmonic series that Euler discovered this cryptic expression for the sum of the reciprocals of primes that began our tour of these infinite sums.

(.141592653589793…)

In fiction by the late Robert Sheckley, the viewpoint character (under strange circumstances) sees empty space filled with vast numbers of “gunmetal gray cubes.” He asks “what are those?” and is told:

“Oh, those are the fundamental building blocks of reality.”

Posted by: Jonathan Vos Post on June 6, 2008 12:54 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

The picture of Europa, at least the enlarged rectangle, seems to show that the lines going / seem to cross OVER \ !! Any one know of an explanation for that?

Posted by: jim stasheff on July 13, 2008 10:03 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Jim, braided rivers, and rivers in ice, are prone to form channels which pass over and under each other.

Posted by: Kea on July 14, 2008 7:25 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Counterintuitive but OK
Reference please

Posted by: jim stasheff on July 14, 2008 1:33 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

$MathML-enabled post (click for more details).$

Interesting question! As far as I know, these cracks don’t arise from ancient rivers. I think they’re caused by stresses in the ice, such as meteors crashing into the surface:

or the motion of plates of ice due to convection of the ice and liquid water underneath:

or the 30-meter-high tides that happen as Europa orbits Jupiter every 85 hours:

(Click on the pictures for more information on each phenomenon.)

I’m not sure I see see any ‘braiding’ phenomena in the cracks… that would be interestingly tricky to explain! But it’s easy to imagine how one crack could form on top of another, given all these processes.

Posted by: John Baez on July 14, 2008 3:22 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

As in braid knot diagrams, are we seeing the `over’ crack really breaking through the lower
or those the lower continue to exist below the upper?

Posted by: jim stasheff on July 15, 2008 1:24 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 265)

Europa and Mars

Posted by: al on December 10, 2009 8:33 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

May 26, 2008