The Globular Extended QFT of the Charged n-Particle: Definition
Posted by Urs Schreiber
After thinking about it for a while (A B C D E F G H I J) it seems that I am finally at a point where I can venture to state a comprehensive formal definition of the structure whose working title was the charged quantum -particle.
The following definition is taken from the beginning of
The Globular Extended QFT of the String propagating on the Classifying Space of a strict 2-Group
which develops one of simplest interesting examples in more detail (to be discussed in a followup post).
The two definitions, discussed in detail below, roughly go like this:
Definition 1. A charged -particle is a setup internal to .
Definition 2. The quantization of a charged -particle is the -functor on obtained by pull-pushing through the correspondence
There is a mystery that demands to be understood:
Mystery: The theory of gerbes with connection in terms of local data exhibits a lot of structural resemblance to state sum models of 2-dimensional quantum field theory, topological as well as conformal.
Why is that?
Does this point to a deeper pattern that we might want to understand?
Can we maybe understand these involved state sum models from first principles?
After a little bit of reflection, I think the pattern is this:
- -Bundles with connection are naturally conceived in terms of parallel transport -functors.
- Coupling these -connections to an -particle amounts to transgressing these -functors to a suitable configuration space.
- Quantizing these charged -particles amounts to pushing the transgressed -functors forward to a point.
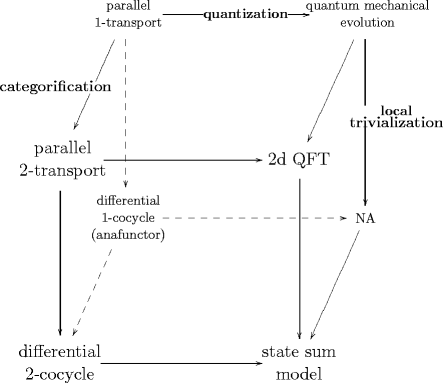
From this point of view, evolution in the quantum field theory of the charged -particle is an -functor that is inherently obtained from the parallel transport -functor that expresses the background field that the particle propagates in.
Both, the original parallel transport -functor as well as the resulting quantum propagation -functor may be locally trivialized. For the former this yields the local description of gerbe holonomy. For the latter this yields the state sum description of QFT.
This situation may be visualized by the following cube, a more detailed description of which is given here.
The essence of the quantization step, going horizontally from left to right in the above cube, is, as I now believe, well captured by the following two definitions.
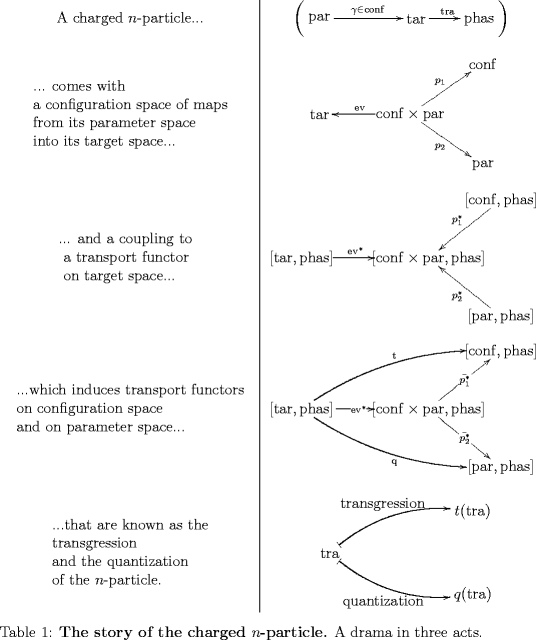
Definition 1. A charged -particle is
- an -category , called parameter space and thought of as modelling the shape and internal structure of the -particle
- an -category, , called target space and thought of as modelling the space that the -particle propagates in
- an -category , being the -category of some notion of -vector spaces
- an -functor , thought of as encoding the parallel transport in an -bundle with connection on target space
- a choice of sub--category , thought of as encoding the configuration space of the -particle.
Of course this data wants to be interpreted internal to a suitable context. Depending on the strictness or weakness of notion of -category one uses, and depending on which additional structures – usually smooth local trivializability – one imposes on , we are dealing with a strict or weak, continuous or smooth -particle, etc.
The main point is now
Definition 2. Given a charged -particle its globular extended quantum field theory is the -functor which is the image of under the morphism indicated in the following diagram.
Here is the obvious evaluation map coming from restricting along the inclusion .
Precomposition with this defines a pull-back -functor and denotes the adjoint of this -functor, a push-forward.
This quantization procedure sends a transport functor on target space to a transport functor on parameter space.
The meaning of the above definition is indicated by the following table.
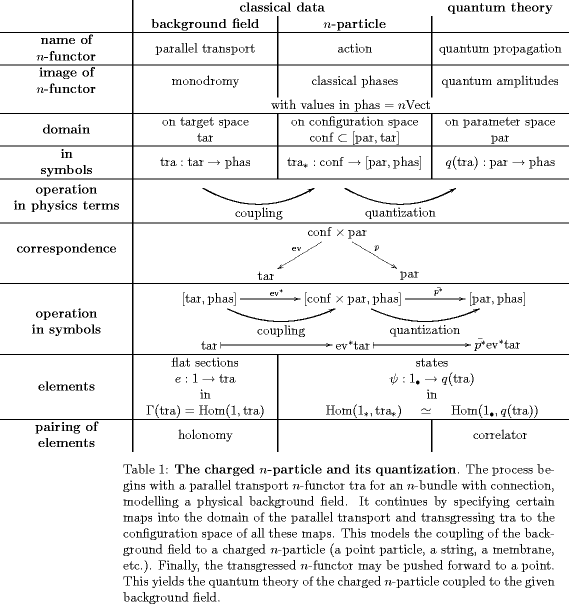
This -functor on parameter space is an extended QFT in that refines the original definition of a QFT as a 1-representation of a cobordism 1-category to an -functorial representation on -vector spaces, which assigns data at all dimensional levels of its domain.
I call the quantized transport a globular extended QFT in order to distinguish it from a bunch of other proposals to define extended QFTs as representations of extended cobordisms categories. In such extended cobordisms categories, objects correspond to collections of points on parameter space (possibly empty), morphisms correspond to collections of arcs in parameter space (possibly empty), and so on.
On the other hand, in a globular extended QFT, an -morphism in the domain is precisely a single -arc in parameter space.
This greatly streamlines the handling of all local aspects of parameter space. It does however come at the cost that no topological nontrivial cobordisms can be handled globally without performing traces, as briefly indicated in section 1.3 of Transport Theory.
Caveat. Without further qualification, the above reproduces only the kinematics of what one ordinarily considers as quantization. Dynamics should follow the same pattern, but is more subtle.
On the other hand, whereas ordinary quantization produces a mere 1-functor the above, being an extended QFT, produces an -functor which contains quite a bit of information, even at the kinematical level. In particular, higher phenomena such as D-branes, string fusion, closed bulk insertions and various other higher structures – that may not even have names yet – are captured.
But more important is this:
there is a phenomenon (a kind of holography) which says, formulated as a principle, roughly that
dynamics of the quantum -particle kinematics of the quantum -particle
This is one of the main motivations for the entire setup discussed here. I shall come back to that later.
Quantization and Transgression.
We can understand the above definitions in a broader context. Notice that, given a charged -particle we can form the diagram and use this to push-pull transport functors on target space either to parameter space – this is the quantization we discussed – or to configuration space. The latter procedure is known as transgression.


Re: The Globular Extended QFT of the Charged n-Particle: Definition
Just a very preliminary comment, provoked by
the definition of quantization of a charged
n-particle via a correspondence. That’s
very similar to one way of generating higher
homotopies, cf. inverting quasiisos (aka quisms).
And that in turn is relevant to the (some kind of ) equivalence of n-groupoids and n-homotopy types.
Some of the talks at the IHP Higher
Structures meeting are now posted at
http://www.math.psu.edu/ping/IHP07/slides/
and hopefully more will be added soon.
Breen’s talk was particularly relevant.