D-Branes from Tin Cans, III: Homs of Homs
Posted by Urs Schreiber
In D-Branes from Tin Cans, I: Arrow Theory of Disks I had started talking about the exercise of finding the right arrow theory for -disk holonomy - in the classical as well as in the quantized world.
For this is quite familiar:
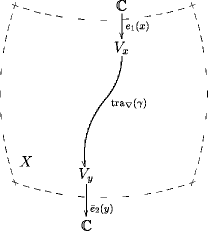
Classically, we have a vector bundle with connection over a space . A path in is a 1-disk. Picking a section of over and over , respectively, i.e. morphisms and amounts to choosing a boundary insertion on the 1-disk.
The disk holonomy of the 1-disk under the transport of with boundary insertions and is the number
where denotes the parallel transport induced by .
There is a quantum version of this. After quantizing the above setup (for instance by pushing it forward to a point) we obtain a vector transport functor on the abstract worldline of the particle, which sends a worldline of length to a morphism in .
Now we can compute the “quantum 1-disk holonomy”. This is known as the (1-)disk correlator. If is a vector in the Hilbert space and is a covector in that space, then the quantum mechanical 1-disk correlator with and as “boundary insertions” looks like this: You may be more familar with this entity in the equivalent notation
The goal of the exercise now is to reformulate this situation arrow-theoretically in such a way, that
a) it is possible to blindly categorify it
b) and that blindly categorifying it yields all the structure we expect to see for 2-disk correlators of strings (= 2-particles), for 3-disk correlators of membranes (= 3-particles), and so on.
Since for higher this will involve lots of tin can diagrams

and since all information about the existence and the nature of D-branes is hopefully contained in these (unless that exercise remains unseccessful), the name of the game is building D-branes from tin cans. Obviously.
When I started doing this exercise, I noticed a curious fact: the arrow-theory for the 2-disk-correlator of the 2-particle looked almost exactly like the arrow-theory for the section of the 3-particle, living over the disk.
This was encouraging, because this relation between states of a 3-dimensional QFT and correlators of a 2-dimensional QFT is precisely one of the things whose better underdstanding motivates going through this exercise here in the first place.
But at that time I did not fully appreciate what was going on. Even though, with hindsight, I could have:
pairing an -section of an -transport functor with an -cosection involves the --functor, as described in the section 1.2 “A Rosetta Stone: arrow theory of quantum mechanics” in On 2D QFT - from Arrows to Disks. But the result of the pairing is itself an ()-transport functor. So we can take its sections, in turn, and pair them. The result is an -transport functors. And so on.
The general mechanism at work here is quite general and not restricted to the funny context that I am applying it to. I bet somewhere out there some category theorists have long ago thought about what I will briefly describe next:
Notes: -Fold Iterated -Pairings
We are faced with the situation where we have a bunch of -functors, here called with a tensor product on them. The tensor unit functor I denote
A “section” of is a morphism
A “cosection” is a morphism
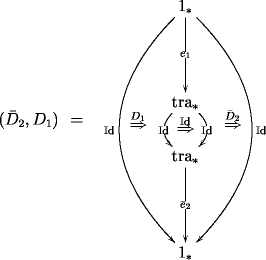
The natural pairing between them, giving rise to the morphism should be thought of as the image of under the Hom--functor
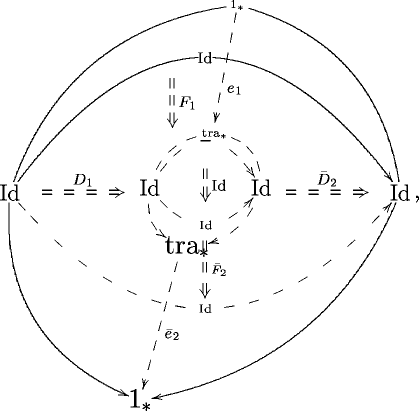
But since is itself monoidal (of course), with tensor unit being , we find that we can, in turn, try to consider sections of the pairing itself. And cosections And hence the corresponding pairing:
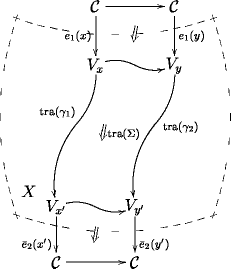
If one thinks about it, one sees that, for 2-functors and in components, this diagram expresses the decoration of disks by diagrams of the sort
In the center we have the value of over the disk in question. On top and bottom we see the “open string insertions” given by the sections and . The semi-disks on the left and right come from the second order sections and . They describe how the endpoints of the string move along the boundary of the disk.
It was exactly this diagram that I considered in Arrow Theory of Disks. But there I added the semi-disks on the left and right more or less “by hand”.
My point here is that we should really be thinking of these D-branes as arising from a “higher order inner product” given by an iterated Hom-construction, in the above sense.
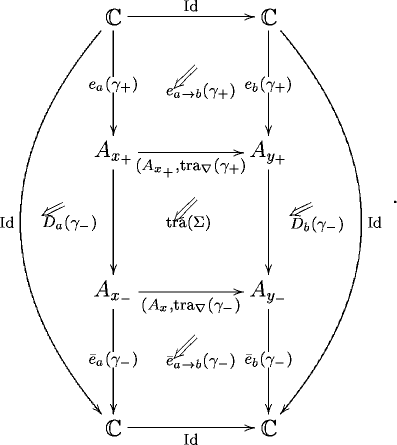
Of course there is then an entire hierarchy of higher order pairings. At level three it looks roughly like this:
Here, now, we have first order sections , second order sections and third-order sections . All of them paired in the indicated way.
It becomes increasingly hard to draw this stuff. In components and for 3-functors, the above globe gives rise to a decoration of disks by diagrams like
This is supposed to remind you of the third diagram on p. 10 in hep-th/0512076. More on that later.

Re: D-Branes from Tin Cans, III: Homs of Homs
This is interesting… I think I’m beginning to understand it. It worries me that it gets difficult to draw as increases though.
Its tough to keep up, but some of Urs’s ideas are slowly starting to sink in, and I’m still wrestling with a few of them.
The one point which Urs (and I) seem to stress is that one should think of bundles (with connection) as transport functors (bottom up) rather than as total space things (top down). So, for instance, one thinks of a vector bundle with connection on a space X as a functor , rather than as a bundle of vector spaces, equipped with a connection.
I’m still not completely certain of where that takes one at the end of the day… perhaps it leads to complications, and I’d like to know what others think about this philosophy.
For instance, take a presheaf on a category C. One can think of it bottom-up as a functor . This is Urs’s (and my) way, and it also happens to be the standard way. You can even think of it as a bundle with connection on C. The space of flat sections of the presheaf is then the space where is the trivial presheaf, which sends everything to .
The space of flat sections of the presheaf is then the space where is the trivial presheaf, which sends everything to .
Alternatively, you can think of it top-down as a discrete fibration . A section is then a functor such that . Passing between these two pictures is a standard exercise in category theory.
Here’s the thing. When you go to higher dimensions, things get a bit more tricky. Given a 2-category , a presheaf of categories on is a weak 2-functor . The space of sections is theen the space of pseduonatural transformations and modifications , where is the trivial presheaf of categories.
Note the words ‘pseudo’ appearing above. It shows that things get a bit tricky, perhaps, in the bottom-up approach.
The top-down approach now says that a presheaf of categories on is a 2-functor . A flat section is a weak 2-functor such that . Passing between the two pictures is called the Grothendieck construction.
Anyhow, the latter picture is perhaps slightly more simple… or perhaps that’s an illusion, since a section is still pseudo stuff.