The n-Category Café

Here’s the conference announcement:

The abstract theory of traces has had a fundamental impact on a variety of fields within mathematics. These range from functional analysis and noncommutative geometry to topology and knot theory, and more recently to logic and theoretical computer science. The theory of traced monoidal categories, due to Joyal, Street and Verity, is an attempt to unify various notions of trace that occur in these diverse branches of mathematics. More recent developments include several theories of partial traces in monoidal categories.

The Logic and Foundations of Computing Group at the University of Ottawa, with funding from the Fields Institute, is proud to host a workshop to explore these topics. The purpose of this workshop is to bring together researchers in these fields to look for common developments, models, and applications of trace theory. Among the applications are various notions of parametrized traces arising in operator algebras, in the theory of feedback and recursion in theoretical computer science, in braid closure in knot theory, and in dynamics of proofs as expressed by Linear Logic and the Geometry of Interaction.

Some invited speakers include:

• Samson Abramsky (Oxford)
• Robin Cockett (Calgary)
• Andre Joyal (UQAM)
• Louis Kauffman (Illinois)
• Mathias Neufang (Carleton)
• Timothy Porter (Bangor)

We will be announcing further speakers shortly. This is intended to be a workshop, with student participation in mind, including introductory lectures. We will have some funding for student travel and accommodation. Students interested in receiving financial aid should contact the organizers by January 30th.

Anyone interested in attending or contributing a talk should contact us by the same date.

You may know about the trace of square matrix, which is a number: just the sum of its diagonal entries. In index notation:

$$Tr(f) = f^i_i$$

where the Einstein summation convention says we sum over the repeated inde $i$.

In quantum physics we often do something more general: we take the ‘partial trace’ of a density matrix describing the state of a two-part system, to get the state of one of the parts. Mathematically, the partial trace of a linear operator

$$f: A \otimes U \to B \otimes U$$

is an operator

$$Tr^U_{A,B}(f): A \to B$$

given by

$$Tr^U_{A,B}(f)^a_b = f^{ai}_{bi}$$

where $i$ runs over a basis of the vector space $U$.

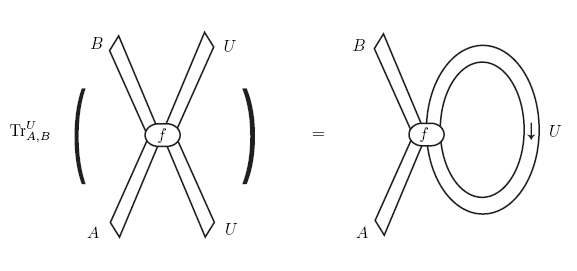
In terms of diagrams, the partial trace looks like this:

Time in this diagram goes up, as in traditional Feynman diagrams. If we’re talking about linear operators, the loop stands for the summation over the repeated index $i$. But these diagrammatic methods are much more general: we can define partial traces in a large class of monoidal categories, including all compact symmetric monoidal categories — but also others! For example, in logic and computer science, partial traces are used to describe ‘fixed points’.

The picture above is from a talk by Paul-André Melliès, which explains some of the uses of traces in logic. Click on it and learn more!