Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

October 26, 2006

Classical vs Quantum Computation (Week 4)

Posted by John Baez

Here are the notes for the latest installment of my course on Classical versus Quantum Computation:

  • Week 4 (Oct. 26) - Currying and uncurrying, evaluation and coevaluation. Basic aspects of the "quantum lambda calculus": so far, the fragment of the lambda calculus that works in any monoidal closed category. The "name" of a morphism. Compact categories.

Last week’s notes are here; next week’s notes are here.

This week we used lambda-terms and also string diagrams to describe “currying” and “uncurrying”. Currying, named after Haskell Curry, is the process of turning a morphism

f:X⊗A→Yf : X \otimes A \to Y

into a morphism

f˜:X→hom(A,Y)\tilde{f}: X \to hom(A,Y)

where hom(A,Y)hom(A,Y) is an object in our category called the “internal hom”. Currying is usually done in a cartesian closed category - but to spice things up a bit, we did our currying in a monoidal closed category. We used currying to construct morphisms called evaluation and coevaluation, and something called the “name” of morphism.

We illustrated these concepts with two main examples. The first is Set\mathrm{Set}: the category of sets, which is cartesian: the tensor product is just the cartesian product, defined by a universal property. The second is Vect, the category of finite-dimensional vector spaces with its usual tensor product. This is compact, meaning that

hom(A,Y)≅Y⊗A *hom(A,Y) \cong Y \otimes A^*

for an object A *A^* called the “dual” of AA.

We saw that string diagrams work a bit better in the compact case than the cartesian case. This is probably why Feynman diagrams were only invented after quantum mechanics, though similar diagrams are also applicable to the category of sets.

Posted at October 26, 2006 9:16 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1005



4 Comments & 2 Trackbacks

Read the post Classical vs Quantum Computation (Week 3)
Weblog: The n-Category Café
Excerpt: Guest lecture by James Dolan: Holodeck strategies and cartesian closed categories.
Tracked: October 26, 2006 9:30 PM

Re: Classical vs Quantum Computation (Week 4)

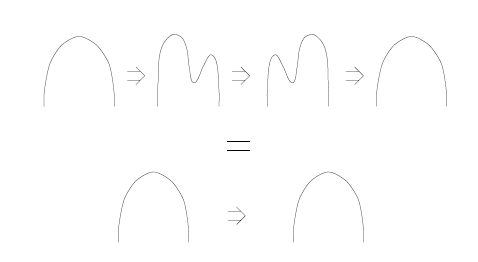
Obvious comment: shouldn’t currying and uncurrying only be inverses up to some sort of natural isomorphism? Or are we already abstract enough for the moment?

Posted by: John Armstrong on October 27, 2006 12:07 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 4)

Currying and uncurrying are maps not between categories but between sets. So, they’re inverses on the nose, not up to natural isomorphism.

In the category of sets, for example, currying is a 1-1 and onto map from the set of functions

{f|f:X×A→Y}\{f |\; f : X \times A \to Y \}

to the set of functions

{f|f:X→Y A}\{f | \; f : X \to Y^A \}

The same idea works in any monoidal closed category, where we use sets of morphisms instead of sets of functions, X⊗AX \otimes A instead of X×AX \times A, and the object hom(A,Y)hom(A,Y) instead of the power set Y AY^A.

Later we may consider monoidal closed 2-categories, and then currying and uncurrying will be functors between categories, and they’ll probably be inverses only up to a natural isomorphism.

Posted by: John Baez on October 27, 2006 1:39 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 4)

Well yes they’re between hom-sets now, but aren’t we supposed to try to replace all sets with categories?

In fact, consider the category of the diagrams you’ve been drawing. You’ve got a couple equalities on the last page (referring to compact categories) that can be weakened as we categorify.

Posted by: John Armstrong on October 27, 2006 2:00 AM | Permalink | Reply to this

Re: Classical vs Quantum Computation (Week 4)

John Armstrong wrote:

Well yes they’re between hom-sets now, but aren’t we supposed to try to replace all sets with categories?

Yes, and then replace all categories with 2-categories, and so on forever. I was talking about what we’ve actually done so far in the course - not what happens when we categorify everything we’ve done.

You’ve got a couple equalities on the last page (referring to compact categories) that can be weakened as we categorify.

Right: the adjunctions

i:1→x⊗x *i : 1 \to x \otimes x^*

e:x *⊗x→1e : x^* \otimes x \to 1

we have in a compact category can be weakened to lax adjunctions in a sort of “compact 2-category”, where the zig-zag equations I drew - also known as triangle equations - get replaced by 2-morphisms.

Either of these 2-morphisms - called triangulators - looks like a process of straightening out a zig-zag:

And, these 2-morphisms satisfy an equation of their own, called the swallowtail identity:

because the top part looks like a swallow’s tail if you draw it in 3 dimensions, instead of drawing the 2d “slices” shown above.

(It was René Thom who first pointed out the importance of the swallowtail catastrophe as part of his classification of catastrophes.)

Categorifying the notion of compact category is crucial when we go from tangles to 2-tangles - and the pictures above come from pages 29-30 of Laurel Langford’s and my paper on 2-tangles.

But, as Todd pointed out, a similar sort of thing is crucial when we try to understand the process of computation. Then, instead of treating beta-reduction and eta-expansion as giving a mere equivalence relation, we think of them as giving 2-morphisms! And again, the equations they satisfy - another version of the triangle equations - get replaced by triangulators, satisfying a swallowtail identity.

I definitely plan to talk about this stuff, later in this year’s course.

Posted by: John Baez on October 27, 2006 3:44 AM | Permalink | Reply to this
Read the post Classical vs Quantum Computation (Week 5)
Weblog: The n-Category Café
Excerpt: The naturality of currying - and a new "bubble" notation for currying and uncurrying.
Tracked: November 2, 2006 10:16 PM

Post a New Comment