Quantum Computation and Symmetric Monoidal Categories
Posted by John Baez
This entry is an excuse to start talking about generalizations of cartesian closed categories (CCCs) suitable for quantum computation. In this discussion, let’s focus on symmetric monoidal categories with duals. Unlike CCCs, these don’t let us duplicate or delete information - as Wootters and Zurek put it, you can’t clone a quantum. But, they permit quantum entanglement, since a state of a two-part system needn’t be just a state of each of its two parts.
All this comes from the fact that the tensor product needn’t be cartesian. On the other hand, the presence of duals for objects lets us draw morphisms as diagrams with lots of input wires and output wires, where we can take any input and bend it around to become an output, or vice versa. These diagrams are a generalization of the Feynman diagrams that physicists know and love:

In quantum field theory, such diagrams describe how particles come in and go out… but in quantum computation, they describe how data flows in and flows out! They’re like “quantum flow charts”.
I’ll start by listing some references….
For the easiest introductions to this stuff, try these:
- John Baez, Quantum quandaries: a category-theoretic perspective.
- John Baez, Higher-dimensional algebra: a language for quantum spacetime.
- Bob Coecke, Kindergarten quantum mechanics
- Bob Coecke, Introducing categories to the practicing physicist.
The first is written for philosophers who only know a little math. All four have lots of pictures - that’s part of the fun here!
To dig a bit deeper, try these:
- Samson Abramsky and Bob Coecke, A categorical semantics of quantum protocols
- Samson Abramsky, Abstract scalars, loops, and free traced and strongly compact closed categories.
- Peter Selinger, Towards a quantum programming language.
- Peter Selinger, Dagger compact closed categories and completely positive maps.
You’ll see lots of diagrammatic reasoning in symmetric monoidal categories here!
There are also attempts to define a “quantum lambda calculus”. Various flavors of this should provide a syntax for various flavors of symmetric monoidal closed category, just as the lambda calculus provides a syntax for cartesian closed categories:
- Peter Selinger and Benoit Valiron, A lambda calculus for quantum computation with classical control.
- Andre van Tonder, A lambda calculus for quantum computation, with simulator program in SCHEME.
- Pablo Arrighi and Gilles Dowek, Linear-algebraic lambda-calculus.
There is also a whole lot of work on linear logic, but I’ll only mention two kinds of linear logic, which both apply to the category of finite-dimensional Hilbert spaces:
-
MILL (multiplicative intuitionistic linear logic) is the syntax for symmetric monoidal closed categories.
-
CMLL (compact multiplicative linear logic) is the syntax for symmetric monoidal categories with duals for objects.
It’s probably worth listing some definitions here. Suppose is a symmetric monoidal category. Then we say:
-
is closed if the functor of tensoring with any object : has a right adjoint, the internal hom In other words, we have a natural isomorphism Here HOM denotes the usual set of morphisms from one object to another, while hom is the “internal hom”, which is an object in our category.
-
has duals for objects if it is closed and for any object there is an object , the dual of , such that for all . If has duals for objects, it’s common for category theorists to say is compact or compact closed; algebraic geometers say it’s rigid.
-
has duals for morphisms if for any morphism there is a morphism such that and all the structural isomorphisms (the associator, the left and right unit laws, and the braiding and balancing) are unitary, where a morphism is unitary when is the inverse of .
-
has duals if it has duals for objects and morphisms. If has duals, Abramsky and Coecke call it strongly compact closed, while Selinger calls it dagger compact closed.
The category of finite-dimensional Hilbert spaces is symmetric monoidal, and it has duals. The same is true for nCob, whose morphisms are n-dimensional cobordisms, like this (for n = 2):
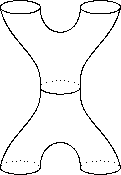
These examples are worked through in Track 1 of my Fall 2000 and Winter 2001 Quantum Gravity Seminar notes, featuring Oz and the Wizard.
I’m also fond of another symmetric monoidal category with duals, where the morphisms are spin foams:
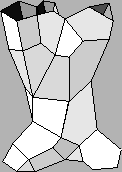
All this stuff is part of a bigger theory, just beginning to be developed, of n-categories with duals and their relation to tangles, cobordisms, and n-Hilbert spaces - see page 22 here to get started on that.
So, what should we talk about? As part of his thesis, Mike Stay wants to work out the syntax for symmetric monoidal categories with duals. It should include all the features of MILL and CMLL. So, one thing we could talk about is those logical systems…


Re: Quantum computation and symmetric monoidal categories
How will this differ from what Abramsky and Duncan have done?