Multiplicative Intuitionistic Linear Logic
Posted by John Baez
The following guest post is by Mike Stay:
I’ve been trying to understand multiplicative intuitionistic linear logic (MILL) from a category-theoretic perspective, and I think I’ve figured out what’s going on — see below. As Richard Guy would say, this is “probably well-known to those who know it.” If you’re one of those, I’d appreciate any references you can think of.
In what follows I’ll say “a MILL,” since we say “a symmetric monoidal closed category”. I’ll use the sequent calculus presentation instead of the natural deduction presentation.
Here are the inference rules, copied from this paper by Benton, Bierman, de Paiva, and Hyland:
A MILL is, apparently, a poset. (Recall that a poset is a category with at most one morphism, called , between any pair of objects). The objects are propositions or resources. if is deducible from .
There are three functors of particular note:
- the tensor product, denoted either by the crossed circle () or by a comma (,). [The comma, as far as I can tell, is a remnant from the standard presentation of intuitionistic (nonlinear) logic.]
the external Hom functor, denoted by a turnstile , written \vdash in TeX. [Note that the Hom set here is really more of a truth value, since given any two objects , either or it isn’t.]
finally, the internal hom functor, denoted by a dash with a circle at the right end , written \multimap in TeX.
A line of the proof is a functor for some . The Hom functor is one of these, but there are more complicated ones, like the first line in the rule:
The inference rules themselves are natural transformations between such functors.
In a symmetric monoidal closed category, we have two natural isomorphisms
satisfying the pentagon and triangle equations. In a poset, these equations are satisfied automatically.
We have a natural isomorphism
satisfying the hexagon equations and . As before, in a poset, these equations are satisfied automatically.
The final natural isomorphism is currying:
Now we have
Identity: this is a natural isomorphism between the constant functor taking every object to the one-element set and the functor that assigns to each object its set of endomorphisms (which, since this is a poset, can contain at most one element). Since identity morphisms always exist, .
Exchange: follows from the braiding.
Cut: this is just composition of morphisms. [Just as there’s a Hom functor, there’s a composition natural transformation.]
: follow from the unit law
: follow from the functoriality of tensor
: this is “internal composition”
: this is exactly currying
As I asked before, if you’ve seen this somewhere, could you post a reference, please?

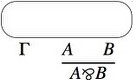 ), why not (?), and bottom (⊥) because they require multiple conclusions (e.g. they’re separated by commas on the right of the turnstile) even when the assumptions have only one conclusion. We also leave out the additive conjuctions to get the multiplicative fragment.
), why not (?), and bottom (⊥) because they require multiple conclusions (e.g. they’re separated by commas on the right of the turnstile) even when the assumptions have only one conclusion. We also leave out the additive conjuctions to get the multiplicative fragment.
Re: Multiplicative Intuitionistic Linear Logic
This seems like the perfect opportunity to make my first post here. I’m a graduate student at McGill university in Montreal, and I’m co-supervised by Michael Barr (of *-autonomous categories fame).
Although I’m a new student this year, and still in the process of figuring these things out, I can nevertheless point you to a paper that I’m sure you’ll find useful.
The paper is written by Robert Seely, who’s an adjunct professor here at McGill , and also a former student of Dr. Barr. It’s called “Linear logic, *-autonomous categories and cofree coalgebras “, and you can find it here…
http://www.math.mcgill.ca/rags/nets/llsac.ps.gz