Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

January 24, 2007

Quantization and Cohomology (Week 11)

Posted by John Baez

In this week’s lecture on Quantization and Cohomology, we’ll start digging deeper into what quantization is really about:
  • Week 11 (Jan. 23) - Action as a functor from a category of “configurations” and “paths” to the real numbers (viewed as a one-object category). Three things physicists do with this functor: find its critical points, find its minima, and integrate its exponential. The analogy between the (classical) principle of least action and the (quantum) principle of path integration. The underlying analogy between the real numbers equipped the operations min and +, and the complex numbers with operations + and ×.

Last week’s notes are here; next week’s notes are here.

Loyal customers of the n-Category Café will see where this is heading! We’ll see how quantization is related to a deformation of rigs. But so far we’re just gathering evidence that this is the case…
Posted at January 24, 2007 1:28 AM UTC

TrackBack URL for this Entry:   http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1124



72 Comments & 4 Trackbacks

Read the post Quantization and Cohomology (Week 10)
Weblog: The n-Category Café
Excerpt: Classical versus quantum mechanics: the Lagrangian and Hamiltonian approaches
Tracked: January 24, 2007 1:52 AM

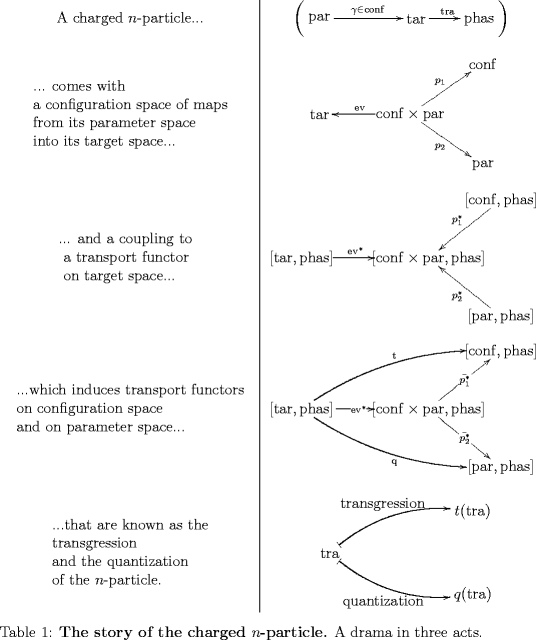
Action as a functor

John writes, in this week’s lecture notes:

What’s really going on?

Is “quantization” some arbitrary trick, or does it have some deeper meaning? Let’s try to dig deeper! What sort of entity is the action?

Incidentally, when reading this I am in the middle of writing up a new refinement of the description of the cube.

I am going to post more details in a while, but I am also trying to condense the main idea into a single table, that organizes all the physics terms and tries to show what’s really going on.

The action functor is featured in the middle column:

I will describe this in more detail in a seperate post and discuss examples.

Two caveats:

(1) The above can be applied blindly only to the kinematical part of the quantization. Dynamics should follow the same pattern, but is more subtle.

But, on the other hand, we have a kind of holography at work, which says that the kinematics of the n-particle looks like the dynamics of the (n−1 )-particle. I am gradually better understanding the details of the formalism behind that, but not sufficiently yet.

I do wonder, though, if, in the end, we want to turn that around and make it a definition: instead of directly saying what the quantum dynamics of the n-particle is, we define it as the quantum kinematics of the (n+1 )-particle.

I’ll need to think about this and work through more examples.

(2) Where the above table says “transgression” I am slightly abusing common terminology.

Ordinary transgression is the composition of a pullback along conf×par→evtar, as above, but then followed by “integrating out parameter space”, by pushing forward along the projection conf×par ↓ conf. As you can see, I don’t use this push-forward in the prodecure indicated in the above table.

Instead, I retain the information of parameter space and get out an extended QFT, namely a functor on par in one step (instead of successively integrating out various parts of parameter space).

So, maybe I shouldn’t say “transgression” in the above. But it actually does, in the end, amount to the same sort of construction. (See this discussion for more on how “my transgression” relates to ordinary transgression)

Posted by: urs on January 24, 2007 11:37 AM | Permalink | Reply to this

Re: Action as a functor

Back here, John said:

the process of reinterpreting ‘dynamics for p-branes’ as ‘statics for (p+1 )-branes’ is a process of categorification, together with Wick rotation. For clarity, we should probably separate this categorification process from the Wick rotation.

Now, you’re saying:

instead of directly saying what the quantum dynamics of the n-particle is, we define it as the quantum kinematics of the (n+1 )-particle.

Do these comments square with each other? Should John have spoken about ‘categorification’ there? Doesn’t it only come in from your perspective when you jump up a level from

dynamics of the n-particle = kinematics of the (n+1 )-particle

to

dynamics of the (n+1 )-particle = kinematics of the (n+2 )-particle

And then I still don’t see why Wick rotation enters in even in classical situations.

Posted by: David Corfield on January 24, 2007 11:59 AM | Permalink | Reply to this

Re: Action as a functor

Do these comments square with each other?

I think they do when you take into account that John was talking about statics, whereas I was talking about kinematics,

which are not exactly the same concepts (though somehow related) – and if you allow for the fact that, as I said, the fully precise statement of a kind of holography that is at work here still escapes me.

The basic motivating fact is this:

it is known that states of Chern-Simons theory encode correlators of WZW theory.

Chern-Simons theory is the theory of a 3-particle (a membrane) propagating on the classifying space BG of a Lie group G, and coupled to a 3-bundle on that.

WZW theory is the theory of a 2-particle (a string) propagating on G itself, and coupled to a 2-bundle on that.

The “correlators” of the WZW theory (i.e. the quantities that encode the dynamics of the WZW 2-particle) are encoded in the states of the CS 3-particle.

This goes back to Witten’s famous paper on CS theory and the Jones polynomial.

More importantly, for our purposes, this fact has been greatly amplified by the FFRS description of WZW theory.

In a way, the FFRS theorem does exactly what I vaguely mentioned under point (1) above: it defines the WZW dynamics in terms of the CS kinematics.

The exercise I am trying to work out is this:

understand the FFRS prescription from first principles and answer a few questions with that understanding.

I think I have completed the puzzle to a degree that the total picture is already visible. But a few pieces are still missing.

Anyway, that’s the motivation for me: n-kinematics vs. (n−1 )-dynamics.

Now, I had never before really thought about what John was discussing in week 2 of Quantization and Cohomology, namely that there is another curious relation between n-particles and (n−1 )-particles: the relation between (n−1 )-dynamics and n-statics.

This is not manifestly the same as the relation (n−1 )-dynamics to n-kinematics. But it feels rather similar! Doesn’t it?

So, I am guessing that in the end, after we understand all this really well, the direct relation between John’s kind of holography and the kind of holography that I am talking about here will become clear. But it’s not fully clear to me at this moment.

Posted by: urs on January 24, 2007 12:31 PM | Permalink | Reply to this

Re: Action as a functor

How would you define ‘kinematics’? Is Wikipedia’s entry good?

In physics, kinematics is the branch of classical mechanics concerned with describing the motions of objects without considering the factors that cause or affect the motion. By contrast, the science of dynamics is concerned with the forces and interactions that produce or affect the motion.

Presumably the restriction to classical mechanics is wrong.

Posted by: David Corfield on January 24, 2007 12:49 PM | Permalink | Reply to this

Re: Action as a functor

How would you define ‘kinematics’?

Classically, a system is specified by

a) a Poisson manifold (X,ω)

b) a certain function h∈C(X) (the “Hamiltonian”).

a) is kinematics. b) is dynamics.

Quantum mechanically, a system is specified by

a) the Hilbert space of states, obtained from sections of a bundle cooked up from (X,ω)

b) an operators ĥ on that space, cooked up from the Hamiltonian function h.

Again, a) is kinematics, while b) is dynamics.

You can see how the quote from the Wikipedia article you gave alludes to this situation by noticing that it is the Hamiltonian which encodes

the forces and interactions that produce or affect the motion

As I tried to indicate in my little table

from the functorial point of view on quantum mechanics we have the slogan

kinematics ↔ objects

dynamics ↔ morphisms

Posted by: urs on January 24, 2007 2:21 PM | Permalink | Reply to this

Re: Action as a functor

John said back in week 1 that (morally) the classical dynamics of point particles is the same as the statics of point particles, except that instead of using X, configuration space, you use PX, path space.

Could one look at statics as that part of dynamics whose solutions are constant paths? That would explain why categorification is relevant in the relation between the dynamics of a point and the statics of a string, as the latter would be a subdiscipline of dynamics of a string.

Posted by: David Corfield on January 24, 2007 6:59 PM | Permalink | Reply to this

Re: Action as a functor

Could one look at statics as that part of dynamics whose solutions are constant paths?

I don’t know, but your saying this immediately reminded me of the (dual?) fact a bundle without connection is like a bundle with connection but involving only constant paths. That is, a principal Gbundle over B is given by a (smooth) anafunctor from the categorially discrete 2space B to the one-object groupoid G (as remarked in Section 2.2.4 of my PhD dissertation), while a principal Gbundle with connection over a space B is given by a (smooth) anafunctor from the 2space of paths in B to the one-object groupoid G (as remarked by Urs). Yet the categorially discrete 2space B is simply the 2space of constant paths in B (as also remarked by Urs).

Posted by: Toby Bartels on January 24, 2007 10:02 PM | Permalink | Reply to this

Re: Action as a functor

Could one look at statics as that part of dynamics whose solutions are constant paths?

I don’t know, but your saying this immediately reminded me of the (dual?) fact a bundle without connection is like a bundle with connection but involving only constant paths.

I am not sure about the relevance of this fact to the dichotomy statics/dynamics.

But I do know that this fact – that parallel transport on constant paths is just a bundle without connection – is at the very heart of that other dichotomy:

kinematics/dynamics.

It goes like this:

on a (“target”) space P 1 (X) we have a vector bundle with connection, (E,∇), given by its parallel transport(-ana-)functor: tra:P 1 (X)→Vect.

Coupling a particle {•} to this bundle amounts to specifying the configurations of the particle in (target) space, i.e. to choosing a sub-category conf⊂[{•},P 1 (X)]≃P 1 (X).

The importance of this choice of sub-category concerns the morphisms. Every isomorphism in P 1 (X) that we retain in conf will make the source and target configuration isomorphic.

So we only want to retain those morphisms in conf that connect “gauge equivalent” configurations.

For instance, if P 1 (X) were the groupoid of paths in an orbifold, regarded itself as a groupoid, we would want to retain all those morphisms in conf that relate points which are identitfied under the orbifold action.

So in particular, if P 1 (X) is just the ordinary path groupoid on an ordinary space, we keep only the identity morphisms in conf, since all points in X we then want to regard as different configurations of our particle {•}.

This is why we would set conf=Disc(X).

Now, the general procedure for finding the quantum kinematics of the particle

{•}

on target space

P 1 (X)

with configurations

Disc(X)

and coupled to the background field

tra:P 1 (X)→Vect

is to pull-push tra through the correspondence

Disc(X)×{•} ev↙ ↘ P 1 (X) {•}.

In our case here this just means that we

- first restrict tra to the constant paths

- and then push it forward to a point.

The result is, indeed, the space of sections of the original vector bundle (this process is described here) which is indeed the quantum kinematics of our particle.

Posted by: urs on January 25, 2007 11:18 AM | Permalink | Reply to this

Re: Action as a functor

But to get straight on my point, is it not obvious that statics can be seen as a part of dynamics? I mean if we have a classical particle in some dynamical situation, we find its path by minimising the action. If the particle is motionless, mustn’t it be because the constant path where it is situated minimises the action?

I’m slightly wary as I note John says elsewhere:

statics, with its minimization of energy, is very different than dynamics, with its minimization of action…If you work hard you can see how statics and dynamics fit together, but if you’re just starting to get an intuition for action, it can be very confusing to think about them both at once, as you seem to be trying to do. Dynamics has an extra dimension - it’s about spacetime, rather than space - and a different thing being mimimized - action, rather than energy.

Posted by: David Corfield on January 25, 2007 11:45 AM | Permalink | Reply to this

Re: Action as a functor

is it not obvious that statics can be seen as a part of dynamics?

Yes, certainly.

If the particle is motionless, mustn’t it be because the constant path where it is situated minimises the action?

Yes, that’s right.

That’s what I can say. Apart from that, I haven’t, myself, thought about the relation n-statics ↔ (n−1 )-dynamics the way that John has. So I cannot really offer much more enlightment on that point at the moment.

Posted by: urs on January 25, 2007 8:03 PM | Permalink | Reply to this

Re: Action as a functor

How’s this for the kinematics/dynamics distinction:

The particular law of actual motion is accompanied by another law which is not the actual law, but which “would be if there were no forces”, as Newton put it. This accompanying law is called inertial or geodesic or spray. The latter merely means that the law is homogenous with respect to the monoid R of time-speedups.

It’s from p. 7 of Lawvere’s Toposes of Laws of Motion.

By the way, two more physics papers by Lawvere are available from IMA preprints. They are

86 State Categories, Closed Categories, and the Existence Semi-Continuous Entropy Functions

87 Functional Remarks on the General Concept of Chaos

Don’t you sometimes get the feeling, reading papers like these, that we should become even more category-minded?

Posted by: David Corfield on January 26, 2007 1:27 PM | Permalink | Reply to this

Re: Action as a functor

Don’t you sometimes get the feeling, reading papers like these, that we should become even more category-minded?

Lawvere took classical mechanics, continuum mechanics, etc., and extracted its category theoretic essence. I have only read fractions of this work, but what I did see I found very inspiring.

What is missing is a similar distillation of quantum physics!

I expect there to be great enlightment to be found in the Lawvere-ification of quantum physics…

Posted by: urs on January 26, 2007 2:01 PM | Permalink | Reply to this

Aristotle on Quantum Field Theory

It’s from p. 7 of Lawvere’ Toposes of Laws of Motion.

I had looked at this quite a while ago. But I had not made it to p. 7, then.

Now I see there, that it says

Already with Aristotle it became customary to analyze Becoming into two aspects, Time and States, with the Time somehow acting on the States.

So Aristotle considered

Becoming:time→Σ(End(states))

I assume he was aware that, for nonrelativistic purposes, time≃Σ(ℝ). And every kid actually thinks of the right hand side here implicitly as Σ(ℝ)≃1 Cob Riem. (Really: that’s how we teach kids , in kindergarten, to think of the reals!)

While I am not an Aristotle specialist, it seems safe to assume that he considered it self-evident that what becomes of a state that has come from another state is the same as what would have become of the latter.

So he knew that Becoming(•→t•→t•)=states→Becoming(t)states→Becoming(t)states.

I conclude that Aristotle knew that Becoming is a functor Becoming:1 Cob Riem→Σ(End(states)).

Posted by: urs on January 26, 2007 3:50 PM | Permalink | Reply to this

Re: Aristotle on Quantum Field Theory

I can go on like this:

Lawvere writes (still p. 7)

the States may involve velocities, or memories, or destinies, but in any case they themselves should be more structured than just points which abstract static Being particularized as configurations.

As if he were on the very verge of finding the need to look at evolution in phase space – and hence maybe the quantum version of what he considers:

So here is the space of configurations conf, and here is a point which abstracts static Being staticBeing:{•}→conf.

Indeed, this is not yet a state, since a state

may involve velocities, or memories, or destinies,

A state, then, is really a point in T *conf, or rather – as we know – a section of a line bundle over conf:

the projection down to conf is Lawvere’s static being, while the remaining information (in the fiber of cotangent space over conf or in the phase of the wave function over staticBeing) is “velocity […] and destiny”.

I cannot quite tell, yet, if this connection to phase space is actually made by Lawvere. Does anyone know?

Posted by: urs on January 26, 2007 4:15 PM | Permalink | Reply to this

Re: Aristotle on Quantum Field Theory

I wrote:

I cannot quite tell, yet, if this connection to phase space is actually made by Lawvere.

On p.9 he writes

Of course, the symplectic or Hamiltonian systems that are also much studied do address this question of states of Becoming versus locations of Being, but in a special way which it may not be possible to construe as a topos

Seems to say that he does not (want to) consider Hamiltonian physics.

On the other hand, while I cannot tell if I fully understand the theorem that follows, it could be that the section s Lawvere is talking about can encode something like momentum or the like.

I think I see the general idea behind the construction of that last theorem, but I find it hard to re-translate the result into something which I am familiar with.

Posted by: urs on January 26, 2007 4:30 PM | Permalink | Reply to this

Re: Aristotle on Quantum Field Theory

So, is he saying that if you just want to study conservative systems, you can do things the Hamiltonian way. But, (1) they don’t form a topos, and (2) most systems we deal with aren’t conservative?

I see some people do work with nonconservative Hamiltonians. Whether that’s enough to regain you a topos, I don’t know.

Do you know how to translate:

all the virtues that that [forming a topos] entails such as internal logic, good exactness, function space of ‘dynamical systems’, etc.

into some tangible examples? All the dynamical maps from one system to another form a dynamical system, hmm.

Posted by: David Corfield on January 27, 2007 3:27 PM | Permalink | Reply to this

Re: Action as a functor

Urs wrote:

Lawvere took classical mechanics, continuum mechanics, etc., and extracted its category theoretic essence.

That’s only partially true. His stuff is definitely worth understanding — I only understand part of it — but it suffers a certain crucial limitation, as you note:

Lawvere wrote:

Of course, the symplectic or Hamiltonian systems that are also much studied do address this question of states of Becoming versus locations of Being, but in a special way which it may not be possible to construe as a topos…

Seems to say that he does not (want to) consider Hamiltonian physics.

Right… because you probably can’t create a topos of Hamiltonian systems!

The problem is that the product of classical phase spaces in Hamiltonian mechanics is not cartesian. There’s an obvious physically correct way to take the product of two symplectic (or Poisson) manifolds M and N and put a symplectic (or Poisson) structure on M×N. But, the obvious candidates for projections

p M:M×N→M p N:M×N→N

are not symplectic (or Poisson) maps! And the obvious candidate for a diagonal map

Δ:M→M×M

suffers from the same defect.

This means you can’t duplicate or delete classical information using a machine whose time evolution is governed by Hamiltonian mechanics.

Lawvere thinks this is a bad thing. I believe he has a strong aversion to noncartesian monoidal structure. As a founder of topos theory, he must feel that intuitionistic logic makes sense — but not the stranger features of logic in a noncartesian monoidal category, where the noncartesian tensor product makes it impossible to duplicate and delete information.

These strange features are well known in the context of quantum mechanics, thanks to the ‘no cloning theorem’ and the violation of Bell’s inequality. But, these features also infect classical mechanics when we take the Hamiltonian approach!

I believe this is why Lawvere prefers to avoid Hamiltonian classical mechanics, and quantum mechanics. He prefers to work with a topos of dynamical systems. So, he sticks to a more Newtonian approach.

I have a different attitude. I think the noncartesian tensor products in the categories of symplectic and Poisson manifolds are a good thing: a fascinating taste of the quantum realm lurking in classical mechanics!

Of course, this is not so surprising if you remember that the Poisson bracket in classical mechanics comes from the commutator of operators in quantum mechanics. And it’s even less surprising once you realize that classical mechanics, like quantum mechanics, can be understood in terms of matrix mechanics — the main difference being a different choice of ground rig.

Since I’m willing to learn logic from Mother Nature, I think we should accept matrix mechanics and learn to love noncartesian monoidal categories.

Posted by: John Baez on January 28, 2007 1:32 AM | Permalink | Reply to this

Re: Action as a functor

So what should we do with nonconservative systems from your perspective?

Posted by: David Corfield on January 28, 2007 8:09 AM | Permalink | Reply to this

Re: Action as a functor

I guess that even though I’ve given up working on quantum gravity, I’m still enough enamored with ‘fundamental physics’ that I don’t spend much time thinking about nonconservative systems. So, I may not be the right person to ask about this. But I’m here, so…

I think it’s one of the great discoveries of humankind that in any system where it seems dissipation is going on — friction, energy turning irreversibly into heat — it’s just an artifact of our ignorance. By taking extra degrees of freedom into account, the system is revealed to be conservative, i.e. described by the Hamiltonian/Lagrangian framework. This is a truly empirical discovery, not a logical necessity (as far as we can tell).

This doesn’t mean that dissipative systems are unimportant. On the contrary, life as we know it is all about entropy increase.

But, it does suggest that a good way to study dissipative systems is as open systems: systems in which we are only describing some of the degrees of freedom.

The working mathematician lives in an open system where he seems able to freely duplicate and delete information. Every math department has its copier room — and next to the copying machine, a waste basket! So, mathematicians, especially logicians, are naturally drawn to cartesian monoidal categories: they describe the logic of our idealized workaday world.

But the physicist can’t help noticing that xerox copies are never perfect, that papers thrown into the wastebasket wind up getting recycled or decomposing in a landfill somewhere, and that it takes electric power to run the copying machine. The idealized workaday world is an open system, part of a bigger physical system described by Hamiltonian/Lagrangian mechanics, in which information cannot be perfectly duplicated or deleted.

So, the topoi that categorical logicians love should somehow sit inside categories with noncartesian monoidal products…

Posted by: John Baez on January 28, 2007 7:10 PM | Permalink | Reply to this

Re: Action as a functor

So, to give a simple case, there you are sitting in a box with a finite number of objects. Your two operations are to dispose of one or to copy one. You think you’re deleting and creating, but really the waste bin is linked to the world outside you box, so adds one to the outside, and the copier is also linked, so when used takes one from the world.

So you thought your world was FinSet, or perhaps Set, but all the time the larger world was a boring fixed number of objects.

So, the topoi that categorical logicians love should somehow sit inside categories with noncartesian monoidal products…

If you think of what’s traced out by 2 points on the x-axis, one starting each side of the origin. The two points converge on the y-axis, and the right hand object passes through to negative x, while the left hand one rebounds back into negative x. So from a God’s eye view there’s a braid being traced out. But seen from the ‘room’ to the left of the y-axis, FinSet is being acted out.

Posted by: David Corfield on January 29, 2007 1:36 PM | Permalink | Reply to this

Re: Action as a functor

David wrote:

So, to give a simple case, there you are sitting in a box with a finite number of objects. Your two operations are to dispose of one or to copy one. You think you’re deleting and creating, but really the waste bin is linked to the world outside you box, so adds one to the outside, and the copier is also linked, so when used takes one from the world.

Right! I’m glad you managed to extract the simple intuition from my obscure and jargonesque comments.

But, there are some subtleties that always confuse me when I try to think about this stuff. For one, there’s a difference between the limitations imposed by reversible computation and the limitations imposed by quantum or even classical computation — where by ‘classical’ I’m referring to the Hamiltonian formalism.

When we talk about reversible physical processes we’re talking about a groupoid with states as objects and processes as morphisms. A category can never have finite products and also be a groupoid unless it has just one object, so reversibility imposes strong limitations on the duplication and deletion of data. Here are two groupoids that show up in the discussion of reversible physical processes:

  • The groupoid of symplectic manifolds and symplectomorphisms.
  • The groupoid of Hilbert spaces and unitary operators.

On the other hand, we can consider possibly irreversible physical processes, but still demand that they fit into some sensible framework for classical or quantum physics… and we still get limitations on duplication and deletion of data, because we get categories that still don’t have finite products, even though they’re not groupoids. Examples include:

  • The category of Poisson manifolds and Poisson maps.
  • The category of Hilbert spaces and bounded linear operators.

Something subtler is going on here!

But, maybe more important than these subtleties is the overall strange idea of taking ‘categories of physical states and processes’ and comparing them to ‘categories of mathematical entities and structure-preserving maps’. The archetype of the latter is the category of sets and functions, and this is where we get our ideas about logic — but then we can transport our ideas about logic to the former sort of category, and get strange notions like ‘quantum logic’ or ‘classical logic’, meaning the logic suitable to the category of (say) Poisson manifolds and Poisson maps.

Should we even be doing this? Should we even try to compare the physical world and the logical world in this way, and be puzzled or at least interested when they differ?

I think we should: I think the ‘disembodied logician’ should be confronted with the fact that his reasoning is a physical process, subject to physical laws. I think something interesting could come of this!

Posted by: John Baez on January 30, 2007 6:16 AM | Permalink | Reply to this

Re: Action as a functor

I’m getting confused now about when you mean the objects of the category to be systems of the same kind, and when you mean the category to have “states as objects and processes as morphisms”.

Your bullet pointed examples suggest the former. But isn’t that the kind of thing you study when you want to show the circle equipped with angle-doubling map is isomorphic to infinite binary strings equipped with the shift map? The morphism between them is not a physical process.

A category of reversible systems is a subcategory of the category of groupoids, which is not itself a groupoid. Symplectic reduction is not reversible.

Posted by: David Corfield on January 30, 2007 8:47 AM | Permalink | Reply to this

Re: Action as a functor

David wrote:

I’m getting confused now about when you mean the objects of the category to be systems of the same kind, and when you mean the category to have “states as objects and processes as morphisms”.

I’m sorry, I meant spaces of states as objects and processes as morphisms.

For example, a Poisson manifold is a space of states in classical mechanics, and a Poisson map describes a physical process. mapping states to states.

But isn’t that the kind of thing you study when you want to show the circle equipped with angle-doubling map is isomorphic to infinite binary strings equipped with the shift map? The morphism between them is not a physical process.

That’s a matter of opinion.

I can imagine building a machine which reads the position of a point on the circle and spits out a string of bits; this machine carries out a physical process implementing the isomorphism you describe.

You may prefer to call this isomorphism a ‘change in our description’ of a physical system, rather than a ‘physical process’. But, trying to decide which isomorphisms are ‘truly physical processes’ and which are ‘just a change of how we describe the same system’ seems to be a loser’s game. One of the big lessons of special relativity was that there’s no cut-and-dried line between dynamics and ‘change of frames of reference’!

Posted by: John Baez on January 31, 2007 7:15 AM | Permalink | Reply to this

Re: Action as a functor

I suppose strictly we’re not allowed angle-doubling/string-shifting as they’re not reversible.

I guess I’m still confused. You say reversible physical processes form a groupoid. What are the connected components of this groupoid? Isomorphism classes of systems? So processes are always redescriptions of the ‘same’ system.

Lawvere’s idea is to form categories whose objects are systems, i.e, spaces acted on by a monoid, T corresponding to time. Choosing T to be a group would relate to reversibility.

Posted by: David Corfield on January 31, 2007 8:24 AM | Permalink | Reply to this

states and processes

Lawvere’s idea is to form categories whose objects are systems, i.e, spaces acted on by a monoid, T corresponding to time.

After thinking about this for a while, I had come to the semi-comclusion that these categorical descriptions of smooth flow ought to also have a reformulation that is a little more hands-on and concrete than this idea of synthetic differentials.

(By the way, is there in any of Lawvere’s papers on this issue a worked example of an application of his abstract topos-theoretic reasoning to something familiar, like a differential equation or something of this sort?)

In a this comment a while ago I describe a way how to formulate the concept of a vector field and of the flow along that vector field in arrow-theoretic terms.

I expect that this is one of the things that Lawvere’s topos-theoretic formulation would also apply to, but the description I mention at the above link seems a little less scary to me – and in fact quite useful.

I have used that to describe the concept of “translation operators” in quantum physics (and indeed in n-quantum physics) on p. 13,14,15 of From Arrows to Disks in a completely arrow-theoretic way.

So from these arrow-theoretic flows one does indeed obtain a process that acts on the space of (n-)states of some system.

That entire section 1.2 of the above document is supposed to provide some arrow-theoretic understanding of “processes on (n-)states of a (n-)quantum system”.

I am not claiming that this is the last word on this issue, but I did find this description helpful and useful. As I try to indicate there, I think that one can understand “n-disk holonomy” and “n-disk correlators” this way #.

Posted by: urs on January 31, 2007 1:38 PM | Permalink | Reply to this

Re: states and processes

By the way, is there in any of Lawvere’s papers on this issue a worked example of an application of his abstract topos-theoretic reasoning to something familiar, like a differential equation or something of this sort?

Back when I was in high school I took a basic physics (E&M) course at a nearby university. Of course I was already into knots, so when I thought about running a current around a knot and letting it find an equilibrium I thought that it might be able to model atoms and molecules. When I brought this silliness to the professor, he was nice enough about it, but told me to show him the hydrogen atom. You need an actual example of some simple, well-known system worked out in detail as proof-of-concept.

So the hydrogen atom is a bit complicated here. Show me Hooke’s Law in topos-theoretical terms.

Posted by: John Armstrong on January 31, 2007 2:30 PM | Permalink | Reply to this

Re: states and processes

I should add that lots of things are made more or less concrete in the work by Anders Kock (see in particular his book).

What I was thinking of, though, was in particular an example of an application of the construction at the very end of Lawvere’s text that we discussed above.

Intuitively, I can sort of see what this is supposed to model, but I would need to work harder to translate that into an actual working example.

Posted by: urs on January 31, 2007 4:00 PM | Permalink | Reply to this

Re: states and processes

John Armstrong wrote:

Back when I was in high school I took a basic physics (E&M) course at a nearby university. Of course I was already into knots, so when I thought about running a current around a knot and letting it find an equilibrium I thought that it might be able to model atoms and molecules. When I brought this silliness to the professor, he was nice enough about it, but told me to show him the hydrogen atom.

I guess you later learned that Kelvin invented knot theory precisely for the same purpose: describing atoms and/or molecules as knotted and/or linked electromagnetic field lines, or ‘vortices in the aether’. And then his pal Tait started compiling a table of knots and links and looking to see if it resembled the periodic table. Of course it did not — but at least this attempt spawned the Tait conjectures, which were solved about a century later using an idea that originated from ideas in mathematical physics: the Jones polynomial. And then, to add to the bizarreness of the whole story, the Jones polynomial turned out to be related to a popular theory of physics saying that everything is made of little bits of string!

So, even if your idea was ‘silliness’, you were at least working your way towards a very fruitful failed theory — Kelvin’s theory of vortex atoms:

Posted by: John Baez on February 1, 2007 2:26 AM | Permalink | Reply to this

Re: states and processes

Kelvin invented knot theory precisely for the same purpose: describing atoms and/or molecules as knotted and/or linked electromagnetic field lines, or ‘vortices in the aether’.

…a very fruitful failed theory — Kelvin’s theory of vortex atoms.

I think its cool that Kelvin really had the `right’ idea, in essence. He just didn’t know how to verbalize it properly. His idea was that atoms are sort of like `knotted electromagnetic field lines’. If one were to go back in time, and offer to him that perhaps he would like to describe it as `the holonomy around a knot of connections on principal G-bundles’ (the modern way to understand gauge theories such as electromagnetism) I have a hunch he might have nodded his head, and said - “Yes! That’s what I was meaning to say!”.

Posted by: postgrad on February 1, 2007 7:28 PM | Permalink | Reply to this

Re: states and processes

I don’t see any evidence Kelvin didn’t fully believe in the ether. There’s no indication that he was thinking metaphorically here. He really meant knotted vortex tubes of ether, like the knotted smoke rings he figured out how to blow.

Posted by: John Armstrong on February 1, 2007 8:12 PM | Permalink | Reply to this

Re: states and processes

I think you’re right - Kelvin probably fully believed in the ether. But then again, when general relativity is phrased in terms of mathematics, I sometimes find it hard to see exactly how the notion of “ether” has been debunked. For, mathematically speaking, we think of the universe as a fixed space-time manifold M, equipped with a Lorentzian metric. Thus, in some sense, there really -is- an “ether”, a fixed background mist in which all worldy phenomena take place : it is precisely the set of points of M.

I quote from the wikipedia article on the “Luminiferous aether”:

…the aether was hypothesized as the absolute and unique frame of reference in which Maxwell’s equations hold. That is, the aether must be “still” universally, otherwise c would vary from place to place.

I can’t help feeling that a lot of the ideas and confusion around the notion of “ether” was tied up with the feeling that somehow there must be a co-ordinate independent way to do geometry, and manifolds in general. Unfortunately I don’t think they had such a theory at the time. Nowadays, as everybody knows, its very easy, and elegant, to formulate Maxwell’s equations in a co-ordinate free way.

Its true that there is no preferred choice of local co-ordinates, which seems to be the standard modern rebuttal of the idea of an “ether”. Nevertheless, there it is : mathematically speaking, its completely true that all wordly phenomena take place in the context of a fixed God-given set M (at least, before one starts doing -quantum- gravity, thereby introducing a bull into the china shop). The “ether” (conceived of as the set M) even has ‘mechanical’ properties : this is nothing but gauge theory, coupled with the ‘modern’ idea of a particle having interal degrees of freedom.

To summarize : its unclear to me exactly how the idea of an “ether” has been rubbished. It seems we just fleshed it out with more precise mathematical notions, more palatable to our modern tastes.

Posted by: postgrad on February 1, 2007 9:06 PM | Permalink | Reply to this

Re: states and processes

A quick self-advertisement. I wrote something about the Kelvin-Tait vortex theory and its relation to their theological views, intended to be part of a popular book. It’s the ‘Smoke Rings’ paper listed here.

Posted by: David Corfield on February 4, 2007 9:30 PM | Permalink | Reply to this

Re: states and processes

Nice! For some reason I’d never read Smoke Rings.

Posted by: John Baez on February 5, 2007 7:14 AM | Permalink | Reply to this

Re: states and processes

Thanks. Note you can also download the figures for the chapter from the same site.

Posted by: David Corfield on February 5, 2007 12:43 PM | Permalink | Reply to this

Re: states and processes

More history of knot theory.

Posted by: David Corfield on March 6, 2007 11:52 AM | Permalink | Reply to this

Re: states and processes

Well, mostly I called it silly because of the fact that I really should have known a bit of history, and that the professor very possibly knew this history already. It’s to his credit that he didn’t throw that back at me.

I just hope that his knowing my father was undergraduate math chair didn’t affect his treatment. Within the department they knew better than to give me any breaks, but in other departments…

Posted by: John Armstrong on February 1, 2007 2:47 AM | Permalink | Reply to this

Re: Action as a functor

Urs wrote:

By the way, is there in any of Lawvere’s papers on this issue a worked example of an application of his abstract topos-theoretic reasoning to something familiar, like a differential equation or something of this sort?

Since you already know about Anders Kock’s work on the Bianchi identity, I assume you’re looking for a topos-theoretic treatment of some differential equations that are honest ‘laws of physics’, not just identities.

I don’t know what’s been done along those lines. I haven’t read all Lawvere’s papers on physics! Here they are, as part of his complete list of papers:

17. Categorical Dynamics in Proceedings of Aarhus May 1978 Open House on Topos Theoretic Methods in Geometry (1979), Aarhus/Denmark.

18. Toward the Description in a Smooth Topos of the Dynamically Possible Motions and Deformations of a Continuous Body, Cahiers de Topologie et Géométrie Différentielle Catégorique XXI (1980), 337-392.

20. State Categories, Closed Categories, and the Existence of Semicontinuous Entropy Functions - IMA Research Report #86, University of Minnesota (1986).

21. Functorial Remarks on the General Concept of Chaos - IMA Research Report #87, University of Minnesota (1986).

22. Introduction to Categories in Continuum Physics, Springer Lecture Notes in Mathematics No. 1174, Springer-Verlag (1986).

36. Unity and Identity of Opposites in Calculus and Physics, Proceedings of ECCT 1994 Tours Conference, Applied Categorical Structures, 4: 167-174 Kluwer Academic Publishers, 1996.

41. Volterra’s functionals and covariant cohesion of space, Supplemento ai Rendiconti del Circolo Matematico di Palermo, Serie II, Numero 64, 2000, Ed. R. Betti and F.W. Lawvere.

43. Categorical algebra for continuum micro physics , Journal of Pure and Applied algebra 175 (2002) 267-287.

I don’t know if he ever tackles specific examples. I remember him discussing #18 in Florence, but the emphasis was on how something like a flexible piece of rubber gives at any time a smooth map f:R→S from the rubber into space which must be one-to-one — a constraint that’s a bit annoying mathematically!

Posted by: John Baez on February 1, 2007 2:29 AM | Permalink | Reply to this

Re: Action as a functor

Since you already know about Anders Kock’s work […]

Yes, I think I understand some of it. But actually, what I understand best is that where the topos-theoretic underpinning is not directly visible.

What is so great about Anders Kock’s papers is that he shows how by simply accepting the fact that infinitesimals exist – pretty much in the “naive” (or not so naive) sense in which they are used throughout physics textbooks anyway – one can access many otherwise apparently subtle concepts by rather elementary reasoning.

I have sort of a feeling for how this notion of “infinitesimal” can be made precise using topos theory. But I have yet to convince myself of this relation in a more thorough way.

Let me be more concrete: I would, for instance, like to see the abstract construction at the very end of Lawvere’s text that we talked about realized in a hands-on way, somehow. (I understand that the second part of Anders Kock’s book should be helpful here, but last time I looked at it I wasn’t mature enough yet to handle it.)

For definiteness, here is what this construction looks like (starting on p. 9):

So we fix some “topos of spaces” (?) and consider, internal to that topos, first of all a diagram T→A.

Here A can be any object of the topos, and T is an object of the kind that Lawvere in this text calls an a.t.o.m (for “amazingly tiny object model” )

An a.t.o.m T is an object (definition on . 6) such that the functor hom(T,⋅) has not just the usual left adjoint T×⋅ but also a right adjoint, denoted (⋅) 1 /T.

I can accept that definition (did I even get it right?) but something inside me is asking for an example.

Okay, so much about what the diagram f:T→A is supposed to be like.

Given this, Lawvere next wants to consider some space X (i.e. an object of our topos), as well as the space hom(A,X) of maps from A to X, and the pullback of these maps along T→A to maps from T to A: f *:hom(A,X)→hom(T,X), which is simply pre-composition with f.

All right. The crucial ingredient now is a choice of section of this map: a morphism going the other way around:

s:hom(T,X)→hom(A,X), or rather one such morphism s(x):hom(T,X)→hom(A,X), for a given x:T→X.

In summary, then, the situation is this: T → A x↘ ↓s(x) X.

As usual, we can think of a map x:T→X as a vector on X. In the “standard example” (the only one I have some understanding of, thanks to Anders Kock) we think of T:={a→b} as the “parameter space of an infinitesimal string” (okay, sorry, that was my own idiosyncratic terminology): two points, a and b, that are infinitesimally close. Then a map T→X is nothing but a choice of two infinitesimally close point on X: hence a vector on X.

As the text explains, in this standard example we are to think of A as something like A={a → b ↓ c}, where a, b are infinitesimal neighbours, as are b and c, so that a and c are second order infinitesimal neighbours (“parameter space of two composable infinitesimal strings”).

So a map s:A→X is something like an infinitesimal square in X, a little loop, to be thought of as the synthetic version of an element in T ∧2 X – as far as I understand.

So, somehow, the above setup is meant to characterize something like a second order ODE, I guess.

It seems like this sentence (p. 10) is meant to explain this:

An actual motion following a law s would be a map (in the dynamical topos) whose domain is a relatively small object idealizing the state space of a clock, i.e. an interval of time equipped with its own (often homogeneous) law which the map must preserve.

But, unfortunately, I don’t really understand what this sentence is saying.

Nor do I understand the message of the theorem that follows.

Theorem: For any given map T→A in a topos with natural number object, where T is an a.t.o.m., the category of all pairs X, s as above, with the obvious motion of morphism, is a topos lex-comonadic over the given topos. In fact, the resulting ‘surjective’ geometric morphism is essential.

It is maybe saying something about second order ODEs (or maybe not). But what is it?

Posted by: urs on February 1, 2007 9:54 AM | Permalink | Reply to this

Re: Action as a functor

An a.t.o.m T is an object […] such that the functor hom(T,⋅) has not just the usual left adjoint T × ⋅ but also a right adjoint, denoted (⋅)1/T. I can accept that definition (did I even get it right?)

Yeah, I think that you got it right. (Of course, I’ve only read the same paper that you have!) Notice that the right adjoint doesn’t really have the algebraic properties that one might associate to such a symbol, so we must be careful with it.

In the “standard example” (the only one I have some understanding of, thanks to Anders Kock) we think of T := {a→b} as […] two points, a and b, that are infinitesimally close. Then a map T→X is nothing but a choice of two infinitesimally close point[s] on X: hence a [tangent] vector on X.

Yeah, that’s the only example that I understand as well, but it bugs me — I don’t think that it has the required right adjoint! That is, given any space Y, what is this alleged space Y1/T such that a map from X to Y1/T is the same thing as a map from hom(T,X) to Y? (Note that hom(T,X) is simply the tangent bundle over X.)

Posted by: Toby Bartels on February 2, 2007 10:45 PM | Permalink | Reply to this

Re: Action as a functor

I’m not an expert, but I guess the existence of the “amazing right adjoint” is a matter of which model of SDG one is working in. According to the book by Moerdijk and Reyes, Models for Smooth Infinitesimal Analysis, which is the book I presently have open on my desk, all the good ones have it.

By “a model of SDG” is meant a topos of sheaves on a site (C,J) where the underlying category C has enough figures to support smooth infinitesimal analysis. Specifically, one often takes C to be the opposite of the category of finitely generated C ∞-rings. (This is supposed to be like algebraic geometry, where one considers sheaves on a site given by the category opposite to finitely generated rings, equipped with a suitable topology.)

C ∞-rings are defined in the style of Lawvere algebraic theories. An ordinary ring (or really an R-algebra) can be thought of as an object A where all polynomial functions R n→R m are interpretable as operations A n→A m. Formally, consider the category Poly whose objects are finite products of copies of R and whose morphisms are polynomial functions between them. Then an R-algebra A is tantamount to a product-preserving functor Poly→Set; the underlying set of A is the value of R under the functor. To get C ∞-rings, apply the same idea except replace polynomial functions with all smooth functions as morphisms.

For example, for any smooth manifold M, the product-preserving functor hom(M,−) gives a C ∞-ring. Hence the category of (finite-dimensional) smooth manifolds is fully embedded in the opposite of (finitely generated) C ∞-rings, also called the category of loci. But the category of loci also admits finite limits (whereas the category of manifolds does not), and hence includes other things like the infinitesimal space T, defined as the locus of intersection between the x-axis and the parabola y=x 2 . Similarly, the representing objects for jet bundles can be obtained as infinitesimal loci.

Okay, so we have this nice category of loci, and a model of SDG allegedly involves sheaves of some sort, Y:Loci op→Set. Let’s forget for the moment what the topology on the site might be, and consider just presheaves. Then, it’s awfully easy to see what Y 1 /T should be: Y 1 /T(L)=Y(L T)! (The walking-tangent vector T is in fact exponentiable in the category of loci.)

Passing to sheaves, it is necessary and sufficient that taking a sheaf to its tangent bundle sheaf preserves colimits of sheaves (and then the same formula for the right adjoint works). That’s true for just about every reasonable topology considered in SDG. See pages 375-376 of the text referenced above for more information.

Posted by: Todd Trimble on February 4, 2007 7:32 PM | Permalink | Reply to this

Re: Action as a functor

Y 1 /T(L)=Y(L T)

Whew — I’m glad someone here understands this stuff. But alas, Todd, I’m still completely in the dark: given a manifold Y, what is the differential-geometric meaning of this space Y 1 /T?

Is it the cotangent bundle of Y, for example? No, of course not.

What is it? Anything familiar? I can’t imagine what it’s like! Some weird space that can only be visualized by people who’ve grown really accustomed to infinitesimals?

In fact, I spent the morning chopping up palm fronds that fell into our yard during the big wind storms we’ve been having, and I kept muttering to myself “maps from TL to Y are the same as maps from L to what?”

(Well, I didn’t use those letters, but you get the idea.)

While wonderful in its own right, this locus hocus pocus doesn’t seem to help me grok Y 1 /T.

Posted by: John Baez on February 4, 2007 11:10 PM | Permalink | Reply to this

Amazing right adjoint

Whew – I’m glad someone around here understands this stuff.

Who, me? Don’t look at me!

But I was really only trying to be responsive to Toby:

Yeah, that’s the only example that I understand as well, but it bugs me – I don’t think that it has the required right adjoint!

by trying to set one context that I think Lawvere might have had in mind, and which has been developed by a number of people as an application of sheaf theory. In terms of “spaces” one is familiar with, what can I say? Y 1 /T is some weird-ass sheaf which behaves like no manifold you’ve ever seen before (its points are points in Y, but its curves are surfaces in Y, just to give a sense of its weirdness).

But in this Grothendieck topos, its existence is no more bizarro than the statement that the tangent bundle functor preserves colimits, which I don’t think is too weird (e.g., sums are preserved, directed colimits are preserved, and so on). That’s all that’s goin