The n-Category Café

I think we should make manifest the following identifications of familiar concepts in quantum theory with functorial notions:

- system/model -
$\begin{array}{ccccccc}\sigma -\text{model:}& & \text{world volume}& \stackrel{\text{field configuration}}{\to }& \text{target space}& \stackrel{\text{exponentiated action}}{\to }& \text{phases}\\ \\ \text{charged particle:}& & 1{\mathrm{Cob}}_{\mathrm{Riem}}& \stackrel{\gamma }{\to }& P_1(X)& \stackrel{{\mathrm{tra}}_{\nabla }}{\to }& \mathrm{Vect}\\ \\ \text{WZW:}& & 2{\mathrm{Cob}}_{\mathrm{conf}}& \stackrel{\Sigma }{\to }& P_2(G)& \stackrel{{\mathrm{tra}}_{{\nabla }_2}}{\to }& 2\mathrm{Vect}\\ \\ \text{general:}& & \text{parameter space}& \stackrel{\text{field configuration}}{\to }& \text{configuration space}& \stackrel{\text{exponentiated action}}{\to }& \text{phases}\\ \\ \text{Chern-Simons:}& & 3\mathrm{Cob}& \stackrel{V}{\to }& P_3(BG)& \stackrel{{\mathrm{tra}}_{{\nabla }_3}}{\to }& 3\mathrm{Vect}\end{array}$

- quantization -
$\begin{array}{ccccc}\text{general:}& & \text{parameter space}& \stackrel{\text{integral of exp. action over field conf.}}{\to }& \text{amplitudes}\\ \\ \text{charged particle:}& & 1\mathrm{Cob}& \stackrel{{⨁}_{\begin{array}{c}\gamma \end{array}}{\gamma }^{*}\mathrm{tra}}{\to }& \mathrm{Hilb}\end{array}$

The main issue is to set up the category of morphisms $n\mathrm{Cob}\to n\mathrm{Vect}$ in a way such that the coproduct

is the $n$-functorial version of the path integral. This is supposed to be an operation which swallows an $n$-vector $n$-transport on a “configuration space” $P_n(X)$, together with a collection of field configurations $n\mathrm{Cob}\to P_n(X)$ and spits out an $n$-QFT $n$-functor:

I think it works like this:

Path integral over a vector transport 1-functor:

I take the liberty of slightly adapting the definition of the various categories involved, just to avoid some technical issues that are irrelevant for the main idea I want to express.

So consider this:

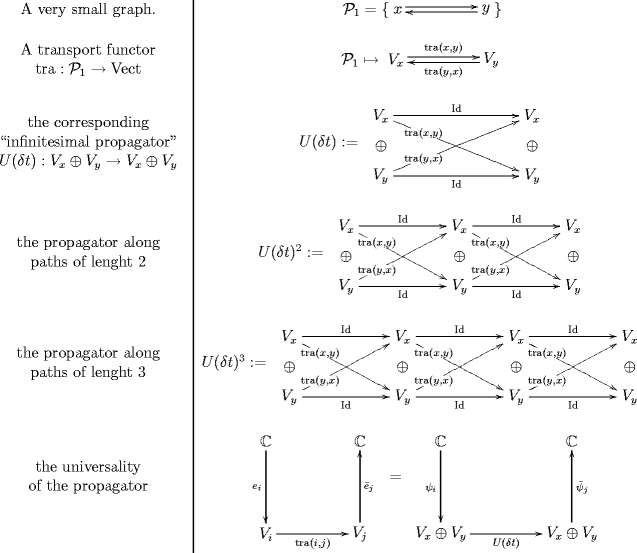
Instead of using the category of 1-dimensional Riemannian cobordisms, I’ll here use the graph

Even though it is abuse of notation, I feel like calling this graph

because this graph will play the role of the time line, or the worldline of a non-relativistic particle.

For $X$ some finite set, let $P_1(X)$ be groupoid freely generated from the free directed graph over $X$. So morphisms here are sequences of elements of $X$, like $x_1\to x_2\to x_3$, and reversing an edge is inverting the corresponding morphism, $(x\to y\to x)={\mathrm{Id}}_x$.

We want to couple our particle to a gauge field on $X$ and then find its quantum dynamics.

Let $E\to X$ be a vector bundle with connection $\nabla$ on $X$. (You should think actually of a complex line bundle, but I won’t need this assumption.) For me, this is a parallel transport functor

This is our “action functional” for a particle coupled to a gauge field.

I take a morphism of graphs

to be a map that sends sequences of edges to sequences of edges, like this

This is a path traced out in $X$, a possible configuration of our “field” (namely the embedding field from the worldline into the target space) on a small piece of worldline.

Composing with our action $\mathrm{tra}$, we find the generalized phase associated with this field configuration

Notice how ${\gamma }^{*}\mathrm{tra}$ naturally extends to a functor from the graph category associated to $1\mathrm{Cob}$ to $\mathrm{Vect}$. (compare Anders Kock’s description of parallel transport #).

Now, the crux of path integral quantization is to “sum” all phases over all possible field configurations.

In our setup everything is categorical and “sum” cannot mean anything but a coproduct-like object. “Field configuration” means “functor $\gamma$” and “phase” means “image of ${\gamma }^{*}\mathrm{tra}$”.

Hence “sum of phases over field configurations” must be some morphism, which I’ll denote

such that all other such functors have morphisms into it

and such that it is the universal object with this property.

In order for this to yield the desired result, one has to find a suitable notion of morphism of graph maps. Something that does seem to work, is the following.

Let the morphisms of the category

be given on each graph edge by something like a naturality square, but with one arrow reversed, like this:

This does not make sense for functors, but it does make sense for graph maps with codomain a category.

Let

be the object in this category which has morphisms into it from every ${\gamma }_i^{*}\mathrm{tra}$, and such that for any other object $Q$ with this propert there is a morphism ${⨁}_{\gamma }{\gamma }^{*}\mathrm{tra}\to Q$.

In order to compute this object, we have to consider commuting diagrams of the form

in $\mathrm{Vect}$.

I think (but you should check it) that this ${\oplus }_{\begin{array}{c}\gamma \end{array}}{\gamma }^{*}\mathrm{tra}$ is precisely the strange kind of sum that we want.

Namely

where $U(\delta t)$ is the $\mid X\mid \times \mid X\mid$-matrix whose $(x,y)$-entry is the linear map

This is indeed the quantum mechnical propagator in the limit where $\delta t$ is a tiny period of time.

As we have seen before, we should think of

as the space of sections of the bundle $E\to X$, hence in fact as the Hilbert space of states of our charged quantum particle.

(In a more detailed derivation we would start with a hermitian vector bundle, which carries a scalar product on each of its fibers. This would then induce the expected scalar product on our Hilbert space of states. Square integrability of sections is one of the technicalities that we are ignoring here, since $\mid X\mid$ is assumed to be finite.)

Moreover, $U(\delta t)$ is evidently that linear endomorphism of this Hilbert space which is obtained by using the classical action along every possible path (of elementary length) between any two points in $X$.

Accordingly, the power

is the linear operator on $H$ which is obtained by a path integral over all paths of total parameter length $n\delta t$.

But that’s precisely the propagator that we are after:

Voilà, the path integral in terms of something like coproducts of transport functors.

Of course the point of this exercise is to go from $n=1$ to $n>1$.

Here is a pdf with some related notes.