The n-Category Café

Lie $n$-algebras in terms of differential algebra

Lie $n$-groups are hard to understand, beyond low $n$ and without restrictive assumptions on their structure.

Lie $n$-algebras are easier to understand:

a (semistrict) Lie $n$-algebra is an $n$-category $g_{(n)}$ internal to $\mathrm{Vect}$ equipped with an antisymmetric bracket functor $$[\cdot ,\cdot ]:g_{(n)}\times g_{(n)}\to g_{(n)}$$ which satisfies the Jacobi identitiy up to coherent equivalence.

What makes this easier to handle is that this entire structure turns out to arrange itself into one single ordinary differential algebra. Or coalgebra, rather.

First, take $V$ to be the vector space of $n$-morphisms of $g_{(n)}$. This is naturally $\mathbb{Z}$-graded: $$V={\oplus }_{k=0}^{n-1}{V}_k.$$ The subspaces $$V_0\oplus \cdots \oplus V_{k-1}$$ are the space of $k$-morphisms of $g_{(n)}$. Alternatively, we may think of $V_k$ alone as the space of $k$-morphisms that start at the vanishing $(k-1)$-morphism.

The funny shift I have inserted ($n-1$ instead of $n$) has very important meaning: we should really think of a Lie $n$-algebra as a one-object Lie $n$-algebroid. This means that what looks like an object in a Lie $n$-algebra is best thought of as a 1-morphism, instead.

To reflect this, we pass from $$V$$ to its suspension $$sV.$$ This is the same vector space, but with the grading shifted by one $$sV={\oplus }_{k=1}^b(\mathrm{sV}{)}_k.$$

So $\mathrm{sV}$ is the space of morphisms of our Lie $n$-algebra $g_{(n)}$. In addition to that information, $g_{(n)}$ carries all the remaining information that make it a monoidal $n$-category:

- source and target maps for all $k$-morphisms

- identity-assigning maps for all $k$-morphisms

- $n$ different composition laws of $n$-morphisms - one of them the bracket functor $[\cdot ,\cdot ]$ itself.

Remarkably, all this information is equivalently encoded in a single operator: a codifferential operator $$D:S^c(sV)\to S^c(sV)$$ of degree -1 on the free graded-co-commutative coalgebra $S^c(sV)$ over $\mathrm{sV}$. All the coherence conditions on the above structures are entirely encoded in the condition that this codifferential squares to 0 $$D^2=0.$$

So

(Semistrict) Lie $n$-algebras are the same as free graded-co-commutative coalgebras on generators in degree $1\le k\le n$ equipped with a nilpotent degree -1 codifferential.

Moreover, free graded-cocommutative coalgras with nilpotent odd codifferential are, in turn, the same as what are called $L_{\mathrm{\infty }}$-algebras. So we may equivalently say

(Semistrict) Lie $n$-algebras are the same as $L_{\mathrm{\infty }}$-algebras concentrated in degree $0\le kkeq(n-1)$.

Furthermore, it is often useful to pass to the dual description: the quasi-free (since the algebra is free, but not the differential) codifferential coalgebra $(S^c(sV),D)$ gives rise to a quasi-free differential algebra $$({\wedge }^{•}(s{V}^{*}),d)$$ simply by setting $$d\omega :=-\omega (D(\cdot ))$$ for all dual elements $\omega \in {\mathrm{sV}}^{*}$.

Hence finally we get

(Semistrict) Lie $n$-algebras are the same as free graded-commutative algebras on generators in degree $1\le k\le n$ equipped with a nilpotent degree +1 codifferential.

This bridge

categorified Lie algebra $\leftrightarrow$ ordinary differential algebra

connects two huge continents. Hence crossing this bridge back and forth is very fruitful. On the left we have conceptual understanding that helps to understand the large-scale properties of our constructions. On the right we have computational control, which allows us to handle the small-scale properties of our constructions.

Universal $n$-Bundles in terms of groupoids

It turns out that for $G_{(n)}$ an $n$-group, one obtains a sequence $$\begin{array}{c}{G}_{(n)}\\ \downarrow \\ {\mathrm{INN}}_0(G_{(n)})\\ \downarrow \\ \Sigma G_{(n)}\end{array}$$ of $n$-groupoids (discussed up to $n=2$ here) which plays the role of the universal $G_{(n)}$-$n$-bundle in the following sense:

For $X$ any space and $Y\to X$ a good cover of it, morphisms of $n$-groupoids $$Y^{[2]}\to \Sigma G_{(n)}$$ classify $G_{(n)}$-$n$-bundles over $X$. The total “space” of such an $n$-bundle, in it’s groupoid incarnation is the pullback $$\begin{array}{ccc}{Y}^{[2]}{\times }_{\Sigma G_{(n)}}{\mathrm{INN}}_0(G_{(n)})& \to & {\mathrm{INN}}_0(G_{(n)})\\ \downarrow & & \downarrow \\ Y^{[2]}& \to & \Sigma G_{(n)}\end{array}.$$ But more its true. As described in more detail (though still not in full detail) in Tangent Categories, the fact that ${\mathrm{INN}}_0(G_{(n)})$ is itself an $(n+1)$-group lets us iterate this construction and form $$\begin{array}{ccccc}{G}_{(n)}& \to & {\mathrm{INN}}_0(G_{(n)})& \to & \Sigma G_{(n)}\\ \downarrow & & \downarrow & {\Downarrow }^{\simeq }& \downarrow \\ {\mathrm{INN}}_0(G_{(n)})& \to & {\mathrm{INN}}_0({\mathrm{INN}}_0(G_{(n)}))& \to & \Sigma {\mathrm{INN}}_0(G_{(n)})\\ \downarrow & {\Downarrow }^{\simeq }& \downarrow \\ \Sigma G_{(n)}& \to & \Sigma {\mathrm{INN}}_0(G_{(n)})\end{array}.$$ Here ${\mathrm{INN}}_0({\mathrm{INN}}_0(G_{(n)}))$ is the total space (in terms of $n+1$-groupoids) of the universal ${\mathrm{INN}}_0(G_{(n)})$-$(n+1)$-bundle. Since ${\mathrm{INN}}_0(G_{(n)})$ is trivializable, so is this $(n+1)$-bundle. We may think of this trivializable $(n+1)$-bundle as the universal trivializable $(n+1)$-bundle which is trivialized by the universal $G_{(n)}$-$n$-bundle.

While important in general, this is not the aspect of the above diagram which shall concern us here. Rather, we note that by pushing our pullback $$\begin{array}{ccc}{Y}^{[2]}{\times }_{\Sigma G_{(n)}}{\mathrm{INN}}_0(G_{(n)})& \to & {\mathrm{INN}}_0(G_{(n)})\\ \downarrow & & \downarrow \\ Y^{[2]}& \to & \Sigma G_{(n)}\end{array}$$ sideways to the right over the above tableau, we choose a connection (in terms of parallel $n$-transport) on our $G_{(n)}$-bundle. The morphism

$$\begin{array}{c}{Y}^{[2]}\\ \downarrow \\ \Sigma G_{(n)}\end{array}$$ which encodes the transition function/descent data of the $n$-bundle may be extended to a morphism $$\begin{array}{ccc}{Y}^{[2]}& \to & C_2(Y)\\ \downarrow & & {\downarrow }^{(g,\mathrm{tra},\mathrm{curv})}\\ \Sigma G_{(n)}& \to & \Sigma {\mathrm{INN}}_0(G_{(n)})\end{array}$$ which encodes

- the nonabelian $G_{(n)}$-cocycle data $g$

- a compatible $G_{(n)}$-connection $\mathrm{tra}$ (hence a nonabelian differential $G_{(n)}$-cocycle)

- and the corresponding curvature $\mathrm{curv}$.

This is the situation in the world of Lie $n$-groupoids. It is conceptually powerful, but hard to deal with in detail. So pass it over our bridge: by looking at this very situation in the world of Lie $n$-algebras and their differential algebra description, we shall arrive at an understanding of characteristic classes of these $n$-bundles.

The general strategy is to some extent summarized in this figure:

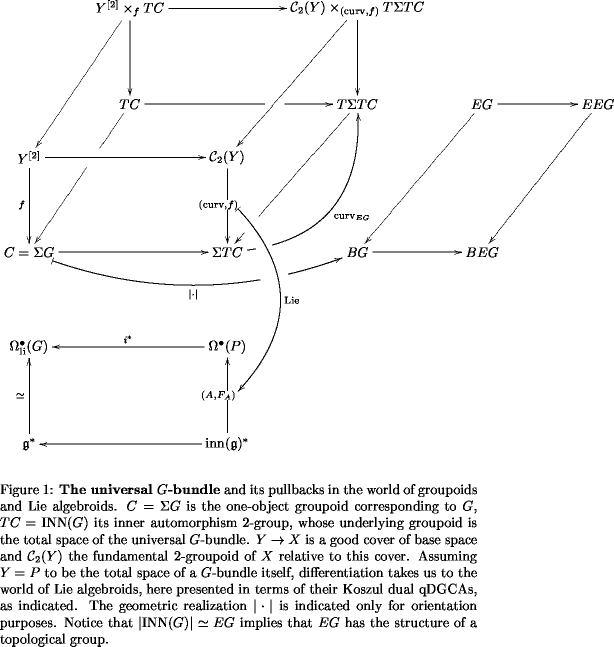
Universal $n$-bundles in terms of Lie $n$-algebras

The Lie $n$-group $G_{(n)}$ turns into the Lie $n$-algebra $g_{(n)}$. The Lie $(n+1)$-group ${\mathrm{INN}}_0(G_{(n)})$ turns into the Lie $(n+1)$-algebra $\mathrm{inn}(g_{(n)})$.

The Lie $n$-algebra invariant polynomials give rise to an abelian Lie $r$-algebra, $$b{g}_{(n)}$$ where $r$ is the degree of the maximal degree invariant polynomial

Notice that $b{g}_{(n)}$ is not the Lie $n$-algebra of $\Sigma G_{(n)}$.

In this business here it is very important to distinguish between $n$-groups regarded as monoidal $(n-1)$-groupoids and the corresponding one-object $n$-groupoids:

- $G_{(n)}$ is an $n$-group. Its Lie $n$-algebra is $g_{(n)}$

- $\Sigma G_{(n)}$ is then, in general, not monoidal any more. Hence it has, in general, no Lie $(n+1)$-algebra associated with it.

But the Lie $r$-algebra $b{g}_{(n)}$ is something like the “best approximation” to this non-existent Lie $n$-algebra:

the graded-commutative algebra underlying $\Sigma G_{(n)}$ is $${\wedge }^{•}(ss{g}_{(n)}^{*}).$$ That there is, in general, no $(n+1)$-group structure on $\Sigma G_{(n)}$ is reflected in the fact that the differential $d_{g_{(n)}}$ coming from $G_{(n)}$ does not extend to the above algebra. On the other hand, the differential $d_{\mathrm{inn}(g_{(n)})}$ can be restricted to this algebra. But it doesn’t close, in general, on that algebra. $b{g}_{(n)}$ corresponds to the maximal subalgebra on which $d_{\mathrm{inn}(g)}$ does vanish. And this turns out to be nothing but the algebra of invariant polynomials on $g_{(n)}$ $$b{g}_{(n)}^{*}:=\mathrm{inv}(g_{(n)})$$

(Compare slide 135-140.)

There is surely a more abstract way to understand what $b{g}_{(n)}$ is. But for the moment let’s use this pedestrian description.

Then $$\begin{array}{c}{g}_{(n)}^{*}\\ \uparrow \\ \mathrm{inn}(g_{(n)}{)}^{*}\\ \uparrow \\ b{g}_{(n)}^{*}\end{array}$$ is supposed to play the role of the universal $g_{(n)}$-$n$-bundle in the world of Lie $n$-algebras.

For $X$ a smooth space, we address a morphism of differential graded algebras

$${\Omega }^{•}(X)\leftarrow b{g}_{(n)}^{*}$$

as a classifying map of $g_{(n)}$-bundles in the world of Lie $n$-algebras. A choice of such morphism is precisely a choice of a closed $r$-form $$K_i\in {\Omega }^{•}(X)$$ on $X$ for each degree $r$ invariant polynomial $$k_i$$ on $g_{(n)}$.

Hence we write

$${\Omega }^{•}(X)\stackrel{\{K_i\}}{\leftarrow }b{g}_{(n)}^{*}.$$

Completing the cone

$$\begin{array}{ccc}& & \mathrm{inn}(g_{(n)}{)}^{*}\\ & & \uparrow \\ {\Omega }^{•}(X)& \stackrel{\{K_i\}}{\leftarrow }& b{g}_{(n)}^{*}\end{array}$$

to the left amounts to choosing a bundle

$$p:P\to X$$

over $X$ together with a $g_{(n)}$-valued connection $A$ on its total space

$$\begin{array}{ccc}{\Omega }^{•}(P)& \stackrel{(A,F_A)}{\leftarrow }& \mathrm{inn}(g_{(n)}{)}^{*}\\ {\uparrow }^{p^{*}}& & \uparrow \\ {\Omega }^{•}(X)& \stackrel{\{K_i\}}{\leftarrow }& b{g}_{(n)}^{*}\end{array}$$

which is such that feeding its $n$-curvatures $F_A$ into all invariant $g_{(n)}$ polynomials $k_i$ produces the previously fixed characteristic classes

$$K_i=k_i(F_A)\in {\Omega }^{•}(X).$$

Demanding furthermore that the pushout of

$$\begin{array}{ccc}& & g_{(n)}^{*}\\ & & \uparrow \\ {\Omega }^{•}(P)& \stackrel{(A,F_A)}{\leftarrow }& \mathrm{inn}(g_{(n)}{)}^{*}\\ {\uparrow }^{p^{*}}& & \uparrow \\ {\Omega }^{•}(X)& \stackrel{\{K_i=k_i(F_A)\}}{\leftarrow }& b{g}_{(n)}^{*}\end{array}$$

exists,

$$\begin{array}{ccc}{\Omega }_{\mathrm{li}}^{•}(\mid G_{(n)}\mid )& \stackrel{\simeq }{\leftarrow }& g_{(n)}^{*}\\ {\uparrow }^{i^{*}}& & \uparrow \\ {\Omega }^{•}(P)& \stackrel{(A,F_A)}{\leftarrow }& \mathrm{inn}(g_{(n)}{)}^{*}\\ {\uparrow }^{p^{*}}& & \uparrow \\ {\Omega }^{•}(X)& \stackrel{\{K_i=k_i(F_A)\}}{\leftarrow }& b{g}_{(n)}^{*}\end{array}$$

amounts to imposing the first Cartan condition: that the connection $A$ restricted to the fibers of $P$ mimics the Lie algebra cohomology of $g_{(n)}$.

(I expect, judging from Jim Stasheff’s hint that requiring the lower of the two squares to also be suitably universal, probably a pushout, will amount to the second Cartan condition, namely the equivariance of $A$. But I am not sure yet how to see this.)

This, then, should be the description of $g_{(n)}$-$n$-bundles in terms of Lie $n$-algebras and their duals.

Characteristic classes of String and $g_{\mu }$-$n$-bundles

It is then an not hard to see that

Proposition 6 For $g$ an ordinary Lie algebra with $(n+1)$-cocycle ${\mu }_k$ which is in transgression with an invariant polynomial $k$ on $g$, and for $$g_{{\mu }_k}$$ the corresponding Baez-Crans type Lie $n$-algebra, we have $$\mathrm{inv}(g_{{\mu }_k})\simeq \mathrm{inv}(g)/k.$$ Hence the characteristic classes of $g_{{\mu }_k}$-$n$-bundles $P\to X$ in the above sense are those of the corresponding $g$-1-bundles, modulo the class coming represented by $K=k(F_A)$ for the given invariant polynomial $k$.

For $g$ simple and $k=⟨\cdot ,\cdot ⟩$ this implies the answer to the nice problem™ that John Baez mentioned in Higher Gauge Theory and Elliptic Cohomology.

There would be more to say. And I intended to say more here. But I am running out of time. So for the moment I end here by relegating all further details to the discussion that can be found in Lie $n$-algebra cohomology.