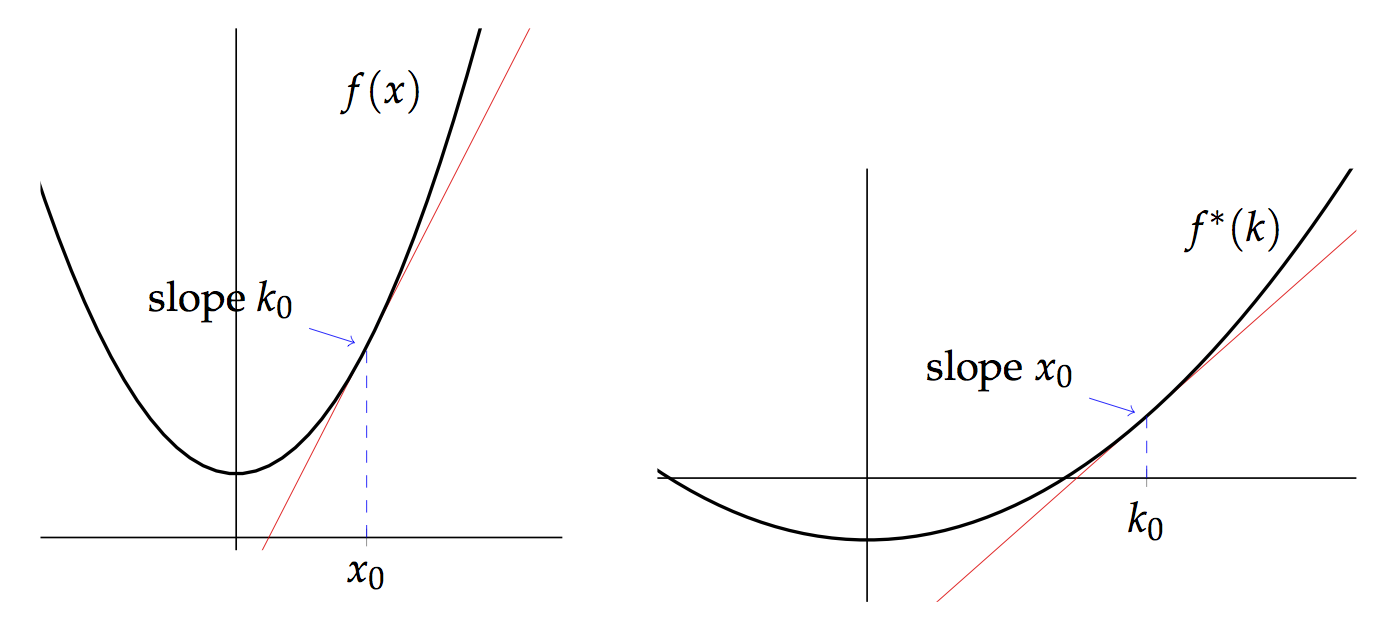April 30, 2014
Should Mathematicians Cooperate with GCHQ? Part 2
Posted by Tom Leinster
A month ago, the newsletter of the London Mathematical Society published an opinion piece of mine, Should mathematicians cooperate with GCHQ?. It has just published an opposing opinion by Richard Pinch, GCHQ’s Strategic Advisor for Mathematics Research and formerly a number theorist at Cambridge.
Pinch’s reply is short and curiously insubstantial. First he makes a couple of general assertions in opposition to what I wrote. But unlike my piece, which linked heavily to sources, he provides no evidence for his assertions. Nor does he dispute any of the specific facts stated in my article. Then he quotes a politician and the director of GCHQ saying that they believe GCHQ operates with integrity. And that’s it.
So it’s almost too flimsy to be worth answering. However, it’s probably worth rebutting even insubstantial arguments when they come from people in positions of influence. Here’s my rebuttal.
April 29, 2014
Homotopy Type Theory: Unified Foundations of Mathematics and Computation
Posted by David Corfield
Congratulations to Mike for being a part of a research team who will receive $7. 5 million to carry on the good work of the IAS Univalent Foundations program. Homotopy Type Theory: Unified Foundations of Mathematics and Computation will run for five years, organised by Steve Awodey at CMU. (Technical portion of the grant proposal is here.)
I hope they’re allowed to use some of that funding to spill into physics a little.
April 28, 2014
On Two-Dimensional Monad Theory
Posted by Emily Riehl
Guest post by Sam van Gool
Monads provide a categorical setting for studying sets with additional structure. Similarly, 2-monads provide a 2-categorical setting for studying categories with additional structure. While there is really only one natural notion of algebra morphism in the context of monads, there are several choices of algebra morphism in the context of 2-monads. The interplay between these different kinds of morphisms is the main focus of the paper that I discuss in this post:
- [BKP] Two-dimensional monad theory, R. Blackwell, G. M. Kelly and A. J. Power, J. Pure and Appl. Algebra 59 (1989), pp. 1-41.
I will give an overview of the results and methods used in this paper. Also, especially towards the end of my post, I will also indicate some points that I think could still be clarified further by formulating some questions, which will hopefully lead to fruitful discussions below.
This post forms the 9th instalment of the series of posts written by participants of the Kan Extension Seminar, of which I’m very glad to be a part. In preparing the post I have greatly benefited from discussions with the other participants in the seminar, and of course with the seminar’s organizer, Emily Riehl. I am very grateful for the enthusiasm, encouragement and guidance that you all offered.
April 27, 2014
New Scientist Article
Posted by Tom Leinster
I’ve got a full-page opinion piece in this week’s New Scientist, on why mathematicians should refuse to cooperate with agencies of mass surveillance. If you’re in the US, UK or Australia, it’s the print edition that came out yesterday.
April 20, 2014
Finite Products Theories
Posted by John Baez
Here’s a classic theorem about finite products theories, also known as algebraic theories or Lawvere theories. You can find it in Toposes, Triples and Theories, but it must go way back to Lawvere’s thesis. In my work with Nina Otter on phylogenetic trees, we need a slight generalization of it… and if true, this generalization must already be known. So I really just want a suitable reference!
Theorem. Suppose is a category with finite products that is single-sorted: every object is a finite product of copies of a single object . Let be the category of models of : that is, product-preserving functors
and natural transformations between these. Let
be the functor sending any model to its underlying set:
Then has a left adjoint
and is equivalent to the category of algebras of the monad
As a result, any model can be written as a coequalizer
where the arrows are built from the counit of the adjunction
in the obvious ways: , and .
April 18, 2014
Elementary Observations on 2-Categorical Limits
Posted by Emily Riehl
Guest post by Christina Vasilakopoulou
In the eighth installment of the Kan Extension Seminar, we discuss the paper “Elementary Observations on 2-Categorical Limits” by G.M. Kelly, published in 1989. Even though Kelly’s classic book Basic Concepts of Enriched Category Theory, which contains the abstract theory related to indexed (or weighted) limits for arbitrary -categories, was available since 1982, the existence of the present article is well-justifiable.
On the one hand, it constitutes an independent account of the fundamental case =, thus it motivates and exemplifies the more general framework through a more gentle, yet meaningful exposition of 2-categorical limits. The explicit construction of specific notable finite limits such as inserters, equifiers etc. promotes the comprehension of the definitions, via a hands-on description. Moreover, these finite limits and particular results concerning 2-categories rather than general enriched categories, such as the construction of the cotensor as a PIE limit, are central for the theory of 2-categories. Lastly, by introducing indexed lax and pseudo limits along with Street’s bilimits, and providing appropriate lax/ pseudo/ bicategorical completeness results, the paper serves also as an indespensable reference for the later “2-Dimensional Monad Theory” by Blackwell, Kelly and Power.
I would like to take this opportunity to thank Emily as well as all the other participants of the Kan Extension Seminar. This has been a unique experience of constant motivation and inspiration for me!
April 16, 2014
Enrichment and the Legendre–Fenchel Transform I
Posted by Simon Willerton
The Legendre–Fenchel transform, or Fenchel transform, or convex conjugation, is, in its naivest form, a duality between convex functions on a vector space and convex functions on the dual space. It is of central importance in convex optimization theory and in physics it is used to switch between Hamiltonian and Lagrangian perspectives.
Suppose that is a real vector space and that is a function then the Fenchel transform is the function defined on the dual vector space by
If you’re a regular reader then you will be unsurprised when I say that I want to show how it naturally arises from enriched category theory constructions. I’ll show that in the next post. In this post I’ll give a little introduction to the Legendre–Fenchel transform.
April 14, 2014
universo.math
Posted by Simon Willerton
A new Spanish language mathematical magazine has been launched: universo.math. Hispanophones should check out the first issue! There are some very interesting looking articles which cover areas from art through politics to research-level mathematics.
The editor-in-chief is my mathematical brother Jacob Mostovoy and he wants it to be a mix of Mathematical Intellingencer, Notices of the AMS and the New Yorker, together with less orthodox ingredients; the aim is to keep the quality high.
Besides Jacob, the contributors to the first issue that I recognise include Alberto Verjovsky, Ernesto Lupercio and Edward Witten, so universo.math seems to be off to a high quality start.
April 7, 2014
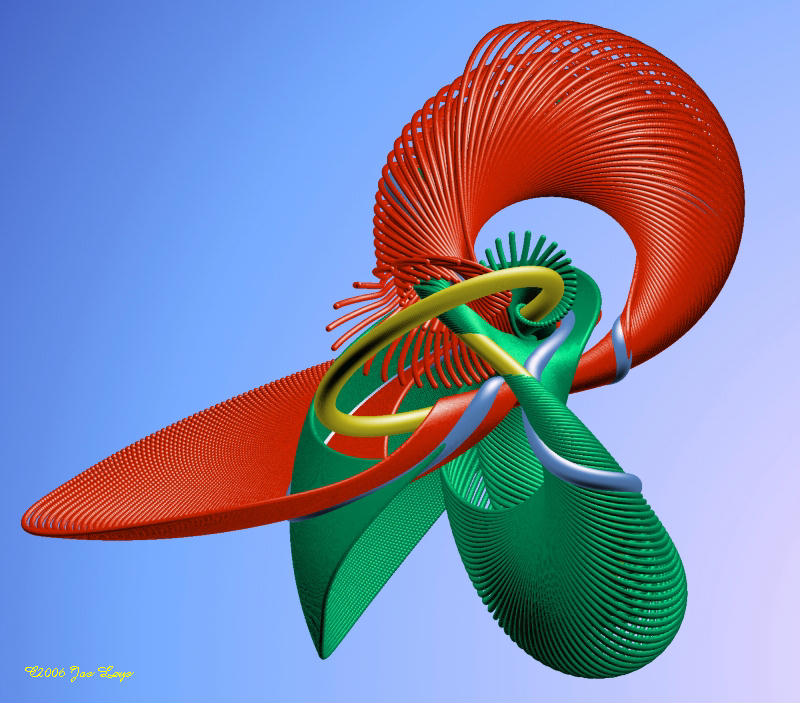
The Modular Flow on the Space of Lattices
Posted by Simon Willerton
Guest post by Bruce Bartlett
The following is the greatest math talk I’ve ever watched!
- Etienne Ghys (with pictures and videos by Jos Leys), Knots and Dynamics, ICM Madrid 2006. [See below the fold for some links.]
I wasn’t actually at the ICM; I watched the online version a few years ago, and the story has haunted me ever since. Simon and I have been playing around with some of this stuff, so let me share some of my enthusiasm for it!
The story I want to tell here is how, via modular flow of lattices in the plane, certain matrices in give rise to knots in the 3-sphere less a trefoil knot. Despite possibly sounding quite scary, this can be easily explained in an elementary yet elegant fashion.
On a Topological Topos
Posted by Emily Riehl
Guest post by Sean Moss
In this post I shall discuss the paper “On a Topological Topos” by Peter Johnstone. The basic problem is that algebraic topology needs a “convenient category of spaces” in which to work: the category of topological spaces has few good categorical properties beyond having all small limits and colimits. Ideally we would like a subcategory, containing most spaces of interest, which is at least cartesian closed, so that there is a useful notion of function space for any pair of objects. A popular choice for a “convenient category” is the full subcategory of consisting of compactly-generated spaces. Another approach is to weaken the notion of topological space, i.e. to embed into a larger category, hopefully with better categorical properties.
A topos is a category with enough good properties (including cartesian closedness) that it acts like the category of sets. Thus a topos acts like a mathematical universe with ‘sets’, ‘functions’ and its own internal logic for manipulating them. It is exciting to think that if a “convenient topos of spaces” could be found, then its logical aspects could be applied to the study of its objects. The set-like nature of toposes might make it seem unlikely that this can happen. For instance, every topos is balanced, but the category of topological spaces is famously not. However, sheaves (the objects in Grothendieck toposes) originate from geometry and already behave somewhat like generalized spaces.
I shall begin by elaborating on this observation about Grothendieck toposes, and briefly examine some previous attempts at a “topological topos”. I shall explore the idea of replacing open sets with convergent sequences and see how this leads us to Johnstone’s topos. Finally I shall describe how Johnstone’s topos is a good setting for homotopy theory.
I would to thank Emily Riehl for organizing the Kan Extension Seminar and for much useful feedback. Thanks go also to the other seminar participants for being a constant source of interesting perspectives, and to Peter Johnstone, for his advice and for writing this incredible paper.
April 1, 2014
Big Data Power
Posted by Tom Leinster
Guest post by Nils Carqueville and Daniel Murfet
(My university probably isn’t alone in encouraging mathematicians and computer scientists to embrace the idea of “big data”, or in more sober terminology, “data science”. Here, Nils Carqueville and Daniel Murfet introduce their really excellent article on big data in whole-population surveillance. —TL)
In recent years Big Data has become an increasingly relevant topic in the economic sector, for intelligence agencies, and for the sciences.
A particularly far-reaching development made possible by Big Data is that of unprecedented mass surveillance. As Alexander Beilinson, Stefan Forcey, Tom Leinster and others have pointed out, the role that mathematicians and computer scientists play here is central. With this in mind last January we wrote an essay on
stressing some of those aspects of the matter that we think deserve more attention or additional elaboration. We hope this to be a useful contribution to the necessary discussion on modern mass surveillance, and we thank Tom for his efforts in this direction, and for allowing us to post here.
 Posts with this logo use
Posts with this logo use