The n-Category Café

Question: What is a Lie derivative really?

Answer (somewhat preliminary): For any given object $C$ in a ($n \gt 1$)-category, Lie derivatives on $C$ are 2-morphisms starting at the identity morphism $$\array{ & \nearrow \searrow^{\mathrm{Id}} \\ C &\Downarrow^f& C \\ & \searrow \nearrow_{t(f)} } \,.$$ These compose using horizontal composition of transformations.

Examples:

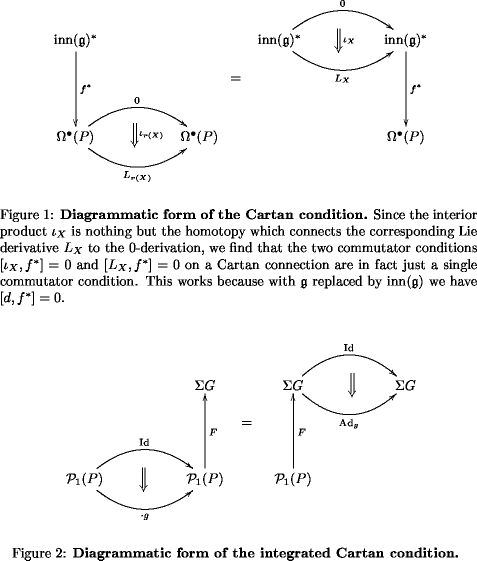
1) ordinary Lie derivatives: Let $$C = (\Omega^\bullet(X),d)$$ be the differential graded commutative algebra of differential forms on a manifold $X$. This is an object in an $\infty$-category (I think) whose morphisms are degree 0-derivations, whose 2-morphisms are chain homotopies of these (hence in particular degree -1 derivations), etc.

Then a Lie derivative as a above is a chain homotopy $i_v$ (contraction with vector field $v \in \Gamma(T X)$) $$\array{ & \nearrow \searrow^{0} \\ (\Omega^\bullet(X),d) &\Downarrow^{\iota_v}& (\Omega^\bullet(X),d) \\ & \searrow \nearrow_{L_v = [d,\iota_v]} } \,.$$

2) the integrated version of that

The above example may be regarded as the Lie algebroid version of the following groupoid situation:

Let $P_1(X)$ be the path groupoid of $X$ (morphisms are thin-homotopy classes of paths in $X$).

In Isham on Arrow Fields I reviewed the discussion of From Arrows to Disks later extended to The Algebra of Observables, that flows along vector fields on $X$ should arrow-theoretically be thought of as transformations: $$t \;\;\; \mapsto \;\;\; \array{ & \nearrow \searrow^{\mathrm{Id}} \\ P_1(X) &\Downarrow^{v}& P_1(X) \\ & \searrow \nearrow_{\exp(v)(t)} } \,.$$ Here, more precisely, the flow is a smooth Lie group homomorphism from the additive group of real numbers to the group of of transformations under horizontal composition as above.

2) the puzzle posed in Derivation Lie 1-Algebras of Lie $n$-Algebras:

Every Lie $n$-algebra $$g_{(n)}$$ can equivalently be conceived as a free graded commutative algebra with a differential on it $$(\wedge^\bullet (sV^*), d_{g_{(n)}})$$ (described here).

This means we have the Lie derivatives $$\array{ & \nearrow \searrow^{0} \\ (\wedge^\bullet sV^*, d_{g_{(n)}}) &\Downarrow^{\iota_x}& (\wedge^\bullet sV^*, d_{g_{(n)}}) \\ & \searrow \nearrow_{L_x = [d,\iota_x]} }$$ for each degree -1 derivation $\iota_x$ on $g_{(n)}$.

I was asking for the integrated version of this. Following this argument I am pretty sure (but still haven’t tried to fully prove this in all detail), that for $G_{(n)}$ a Lie $n$-group integrating $g_{(n)}$, the corresponding Lie group is that of the transformations

$$\array{ & \nearrow \searrow^{\mathrm{Id}} \\ \Sigma(G_{(n)}) &\Downarrow^{f}& \Sigma(G_{(n)}) \\ & \searrow \nearrow_{f(f)} } \,.$$

There is a story to be told how these three examples taken together help to find the answer to

What is a Cartan connection, really?

Answering this solves the problem

What is a $g_{(n)}$-connection , for $g_{(n)}$ any Lie $n$-algebra?

But that story will be told elsehere.