Derivation Lie 1-Algebras of Lie n-Algebras
Posted by Urs Schreiber
Here is a fact which should be important, but whose true meaning is not entirely clear to me at the moment:
To every Lie -algebra is canonically associated an ordinary Lie algebra .
This Lie 1-algebra is, in some sense, a Lie 1-algebra of derivations of the Lie -algebra. But it is not the derivation Lie -algebra .
What is , conceptually?
Why does it exist, as an ordinary Lie algebra?
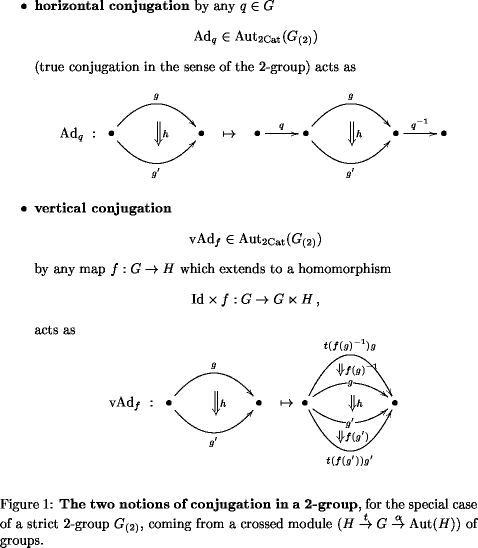
What is its analog at the level of Lie -groups?
Below I give the detailed description and mention applications where this is relevant.
For more details see section 3.3.1 of
and section 5.3 of
(which has grown out of the original zoo).
The Definition
This is how to canonically associate a Lie 1-algebra to any Lie -algebra (it’s a perfectly standard construction in homological algebra, though not usually interpreted in terms of Lie -algebras):
Conceive the Lie -algebra as a free graded commutative algebra with a graded differential of degree 1 on it, such that . Then on the vector space of graded derivations of degree -1 on the algebra we have the following Lie bracket where is the “Lie derivative” associated with .
First Examples
I need to work out more examples. But it’s tedious. So far I have this:
1) Let be an ordinary Lie algebra. Then it coincides with its own Lie algebra of derivations as defined above.
2) Let
be the Lie 2-algebra corresponding to an infinitesimal crossed module. Then for the above Lie 1-algebra associated with it I find this funny result:
As a vector space, it is This is equipped with a semidirect sum structure of Lie algebras:
The bracket on the first -summand is that of . The bracket on the summand is given by for all and all .
The action of on is given by for all , and .
3) Let, for simple, be the Baez-Crans Lie 2-algebra coming from the canonical 3-cocycle. Then the above Lie algebra is the direct sum Lie algebra
Why I think understanding this is important
My motivation for looking into this is Castellani’s observation that there is a Lie 1-algebra of derivations of the supergravity Lie 3-algebra, which coincides with the famous “M-algebra” polyvector extension of the super-Poincaré Lie algebra.
Now, what Castellani does is not precisely what I consider above. Rather, he looks at something like derivations acting on connections with values in the Lie 3-algebra. But since it is still not entirely clear to me what the operation he uses really is, conceptually (in particular how it extends from generators to the entire differential algebra), I thought it would be worthwhile first considering the related problem described above.
In any case, there seems to be something going on here relating Lie algebra cocycles and Lie algebra extensions in two ways: extensions as Lie 1-algebras and extensions as Lie -algebras. Something important is going on, but it escapes me presently.
What does it correspond to at the level of Lie -groups?
The problem is that the Lie 1-algebras discussed here are obtained from the Lie -algebra in a non-conceptual manner: it so happens that it is convenient to compute with Lie -algebras by instead using the equivalent differential graded algebras. But then one runs the risk of performing steps whose categorical interpretation is not transparent. This is what is happening here.
So I started making educated guesses for what is going on. Before I computed the derivation Lie 1-algebra for the case I was sure I would simply get the Lie algebra of the Lie group of morphisms of the Lie 2-group coming from an integrating crossed module . That would have been the Lie algebra of the semidirect product group .
Clearly, this is not unrelated to the true result mentioned above, but still different from that.
So what’s going on?

Re: Derivation Lie 1-Algebras of Lie n-Algebras
If I understand correctly, a Lie n-algebra is just (the dual of) an FDA. An FDA is typically defined as a system of form equations w = 0, where w is some collection of forms, e.g. Castellani’s (3.1). The group of diffeomorphisms acts on w, and the diffeos which preserve the equation w = 0 is evidently a subgroup. Is not this what you have found?
One can quite generally describe Lie groups as subgroups of the diffeomorphism group which preserve some structure. E.g., the Poincare group preserves the length element ds^2, and the conformal group preserves the lightcone ds^2 = 0.