Chern Lie (2n+1)-Algebras
Posted by Urs Schreiber
I mentioned Lie -algebras coming from invariant symmetric polynomials of degree on some Lie algebra in Zoo of Lie -Algebras.
Since it is a really simple and short computation, I want to give here all the details needed to understand it.
This is the picture I want to establish:
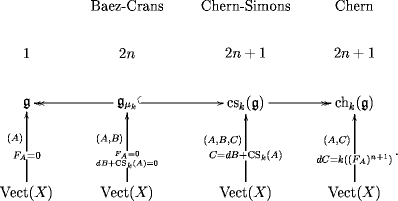
This is really a weakly (up to homotopy) exact sequence of Lie -algbras whenever induces a -cocycle .
I’ll work here entirely in terms of differential graded commutative algebras, which are free as graded commutative algebras. Alternatively I could give the codifferential coalgebra picture, which has the advantage that it is practical to write everything down without first choosing a basis. But here I won’t. This means I’ll chose a basis for displaying my formulas. Those who don’t like this can easily translate back to the coalgebra picture.
Basic machinery
So, fix some Lie algebra . Write for a copy of the underlying vector space, but considered as being in degree 1, and write for yet another copy of that vector space, but considered now in degree 2. And so on.
Choose a basis of and let be the corresponding dual basis of . Let be the structure constants of in that basis.
Then, on the free graded commutative algebra the following defines a graded differential of degree +1 such that : The differential algebra is the Lie algebra , in its dual incarnation.
Next, consider the free differential graded algebra generated from two copies of , in degree 1 and 2: Write for the dual basis of , but regarded as being in degree 2. Then and defines again a differential of degree +1 and squaring to 0. The differential algebra is the (dual incarnation of the) Lie 2-algebra called
Cocycles and Invariant Polynomials in -cohomology
It will be very convenient to formulate the concept of Lie algebra cohomology in terms of the above differential algebras. (The following is my observation. If it is well known, which it should be in as far as it is right, I am not aware of the relevant literature.)
- A coycle of degree on the Lie algebra is nothing but a -closed polynomial of degree in :
- A symmetric invariant polynomial of degree on is nothing but a -closed polynomial in :
Notice that, in components, is necessarily given by an antisymmetric and by a symmetric tensor, since the are odd graded while the are even graded.
- Given an invariant polynomial as above, it may happen that is a cocycle. If so, I’ll call this cocycle
Baez-Crans Lie -algebras from -cocycles
Given an -cocycle on , it is easy to extended the differential algebra to one whose differential is defined on by as before and where is the canonical basis of , i.e nothing but a linear form on , regarded as being in degree .
Clearly, by the defining property of .
The resulting differential algebra is the (dual incarnation of the ) Baez-Crans Lie -algebra
Chern Lie -algebras from degree -invariant polynomials
Quite analogously, we can construct a nilpotent differential from any invariant polynomial. All we have to do is to allow for the existence of even-graded elements. So we essentially repeat the above construction, but building on instead of on itself.
So, given a degree -invariant polynomial on , it is easy to extended the differential algebra to one whose differential is defined on by as before and where is the canonical basis of , i.e nothing but a linear form on , regarded as being in degree .
Clearly, by the defining property of .
The resulting differential algebra might be called the (dual incarnation of the ) Chern Lie -algebra
Chern-Simons Lie -algebras from degree -invariant polynomials with associated cocycle
When the invariant degree polynomial induces a -cocycle as described above, there is a mixture of these two constructions.
Assume that the polynomial has the special property that there is a polynomial (meaning it’s a polynomial in the s and in the s which is at least linear in the s) such that This is for instance the case whenever the polynomial admits a Chern-Simons form.
(I was about to say something supposedly profound about if this is always possible and things like that, when I ran into a mistake I was making concerning these issues. So for the moment I won’t say anything further about this issue, except for noticing that there is at least one interesting class of polynomials where this does work.)
Given the above situation, it is easy to extended the differential algebra to one whose differential is defined on by as before and
Clearly, by the defining property of and Q.
The resulting differential algebra might be called the (dual incarnation of the ) Chern-Simons Lie -algebra
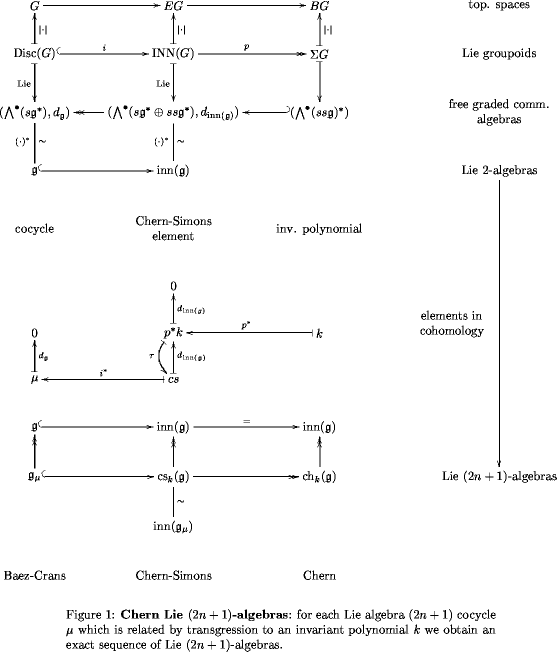
The canonical morphisms between these Lie -algebras
We the obvious inclusion and the obvious surjection Its is easy to check that both these maps commute with the respective differentials and that their composite is homotopic to the zero map.
This means that we have an exact sequence of Lie -algebras

Re: Chern Lie (2n+1)-Algebras
Urs wrote:
If I understand what you’re talking about — my eyes glaze over when I look at those scary formulas — you’re wondering if every degree- invariant polynomial on the Lie algebra comes from an element in the Lie algebra cohomology .
Here’s a nicer way to say the same thing: you’re wondering if every element of the cohomology of comes from an element of the cohomology of via the ‘transgression’ map
(Following Jim, I’ve decided to reverse the direction of my transgression map. I’ve also reindexed things to match your post.)
If that’s what you’re wondering, the answer is no!
As I tried to explain, and Jim explained much better, when is a compact Lie group the only guys in the image of
are the so-called ‘primitive’ elements: linear combinations of the guys that generate as a polynomial algebra.
For this means: linear combinations of the Chern classes .
But not, for example, .
So, for example, when , we get a so-called Baez–Crans Lie 2-algebra out of the 2nd Chern class , because this has a corresponding Chern–Simons form. In other words, it comes from an element of Lie algebra cohomology via transgression.
We also get a Lie 4-algebra from the 3rd Chern class, and a Lie 6-algebra from the 4th Chern class, and so on, because all these have corresponding Chern–Simons forms.
But, we wouldn’t get a Lie 4-algebra from , because this element isn’t ‘primitive’.
If I’m failing to understand you, or you’re failing to understand me, please let me know. I could also easily be making some mistakes with all these numbers…
The nice thing is, all the primitive elements of the cohomology of have been listed in that darn table I keep mentioning on page 11 here, so we can completely understand what’s going on, at least when is a compact simply-connected simple Lie group.