From the Icosahedron to E8
Posted by John Baez
Here’s a draft of a little thing I’m writing for the Newsletter of the London Mathematical Society. The regular icosahedron is connected to many ‘exceptional objects’ in mathematics, and here I describe two ways of using it to construct . One uses a subring of the quaternions called the ‘icosians’, while the other uses Du Val’s work on the resolution of Kleinian singularities. I leave it as a challenge to find the connection between these two constructions!
(Dedicated readers of this blog may recall that I was struggling with the second construction in July. David Speyer helped me a lot, but I got distracted by other work and the discussion fizzled. Now I’ve made more progress… but I’ve realized that the details would never fit in the Newsletter, so I’m afraid anyone interested will have to wait a bit longer.)
You can get a PDF version here:
But blogs are more fun.
From the Icosahedron to E8
In mathematics, every sufficiently beautiful object is connected to all others. Many exciting adventures, of various levels of difficulty, can be had by following these connections. Take, for example, the icosahedron — that is, the regular icosahedron, one of the five Platonic solids. Starting from this it is just a hop, skip and a jump to the lattice, a wonderful pattern of points in 8 dimensions! As we explore this connection we shall see that it also ties together many other remarkable entities: the golden ratio, the quaternions, the quintic equation, a highly symmetrical 4-dimensional shape called the 600-cell, and a manifold called the Poincaré homology 3-sphere.
Indeed, the main problem with these adventures is knowing where to stop. The story we shall tell is just a snippet of a longer one involving the McKay correspondence and quiver representations. It would be easy to bring in the octonions, exceptional Lie groups, and more. But it can be enjoyed without these digressions, so let us introduce the protagonists without further ado.
The icosahedron has a long history. According to a comment in Euclid’s Elements it was discovered by Plato’s friend Theaetetus, a geometer who lived from roughly 415 to 369 BC. Since Theaetetus is believed to have classified the Platonic solids, he may have found the icosahedron as part of this project. If so, it is one of the earliest mathematical objects discovered as part of a classification theorem. In any event, it was known to Plato: in his Timaeus, he argued that water comes in atoms of this shape.
The icosahedron has 20 triangular faces, 30 edges, and 12 vertices. We can take the vertices to be the four points
and all those obtained from these by cyclic permutations of the coordinates, where
is the golden ratio. Thus, we can group the vertices into three orthogonal golden rectangles: rectangles whose proportions are to 1.
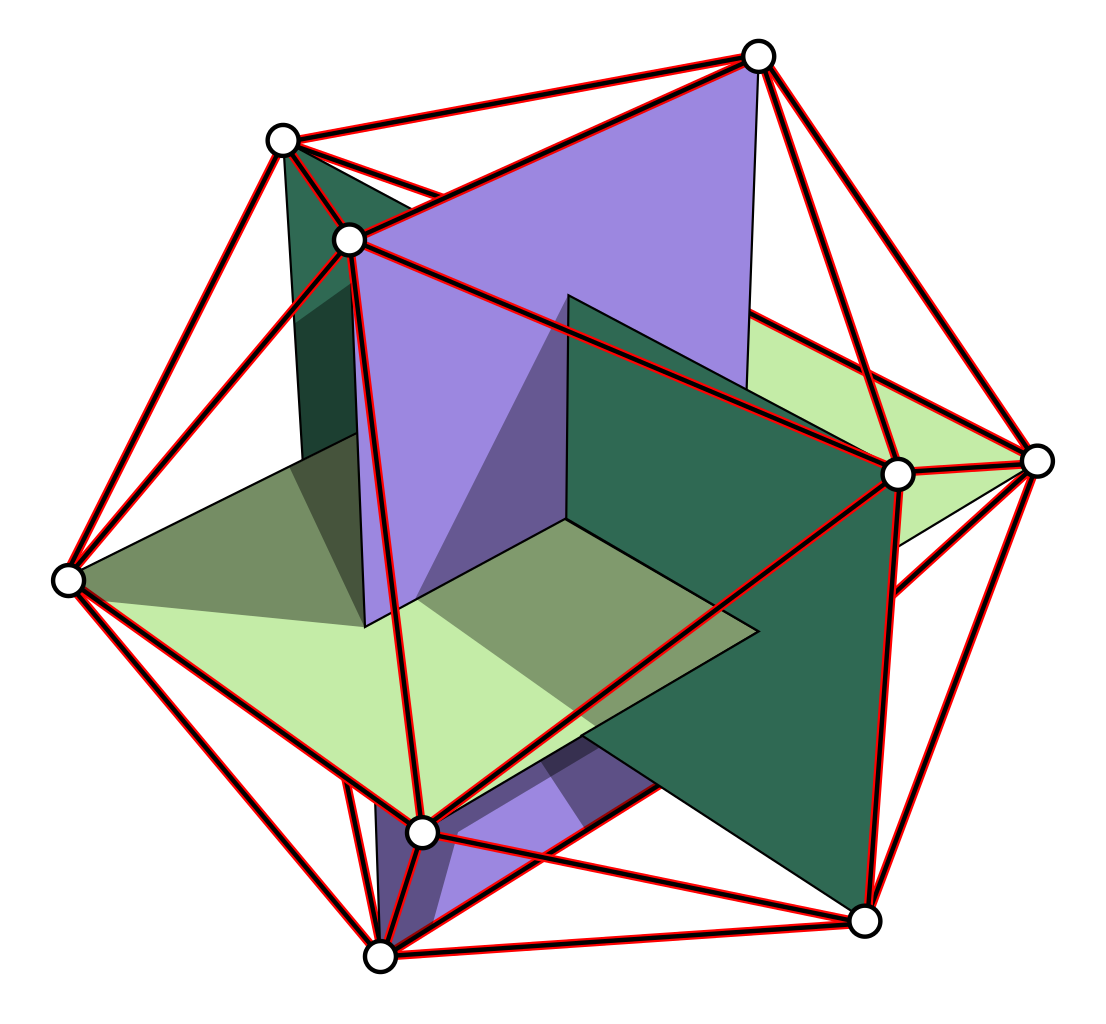
In fact, there are five ways to do this. The rotational symmetries of the icosahedron permute these five ways, and any nontrivial rotation gives a nontrivial permutation. The rotational symmetry group of the icosahedron is thus a subgroup of . Moreover, this subgroup has 60 elements. After all, any rotation is determined by what it does to a chosen face of the icosahedron: it can map this face to any of the 20 faces, and it can do so in 3 ways. The rotational symmetry group of the icosahedron is therefore a 60-element subgroup of . Group theory therefore tells us that it must be the alternating group .
The lattice is harder to visualize than the icosahedron, but still easy to characterize. Take a bunch of equal-sized spheres in 8 dimensions. Get as many of these spheres to touch a single sphere as you possibly can. Then, get as many to touch those spheres as you possibly can, and so on. Unlike in 3 dimensions, where there is “wiggle room”, you have no choice about how to proceed, except for an overall rotation and translation. The balls will inevitably be centered at points of the lattice!
We can also characterize the lattice as the one giving the densest packing of spheres among all lattices in 8 dimensions. This packing was long suspected to be optimal even among those that do not arise from lattices — but this fact was proved only in 2016, by the young mathematician Maryna Viazovska [V].
We can also describe the lattice more explicitly. In suitable coordinates, it consists of vectors for which:
• the components are either all integers or all integers plus , and
• the components sum to an even number.
This lattice consists of all integral linear combinations of the 8 rows of this matrix:
The inner product of any row vector with itself is 2, while the inner product of distinct row vectors is either 0 or -1. Thus, any two of these vectors lie at an angle of either 90° or 120° from each other. If we draw a dot for each vector, and connect two dots by an edge when the angle between their vectors is 120° we get this pattern:
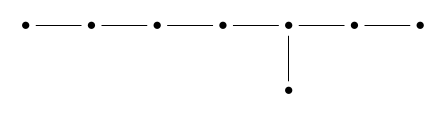
This is called the Dynkin diagram. In the first part of our story we shall find the lattice hiding in the icosahedron; in the second part, we shall find this diagram. The two parts of this story must be related — but the relation remains mysterious, at least to me.
The Icosians
The quickest route from the icosahedron to goes through the fourth dimension. The symmetries of the icosahedron can be described using certain quaternions; the integer linear combinations of these form a subring of the quaternions called the ‘icosians’, but the icosians can be reinterpreted as a lattice in 8 dimensions, and this is the lattice [CS]. Let us see how this works. The quaternions, discovered by Hamilton, are a 4-dimensional algebra
with multiplication given as follows:
It is a normed division algebra, meaning that the norm
obeys
for all . The unit sphere in is thus a group, often called because its elements can be identified with unitary matrices with determinant 1. This group acts as rotations of 3-dimensional Euclidean space, since we can see any point in as a purely imaginary quaternion , and the quaternion is then purely imaginary for any . Indeed, this action gives a double cover
where is the group of rotations of .
We can thus take any Platonic solid, look at its group of rotational symmetries, get a subgroup of , and take its double cover in . If we do this starting with the icosahedron, we see that the -element group is covered by a 120-element group , called the binary icosahedral group.
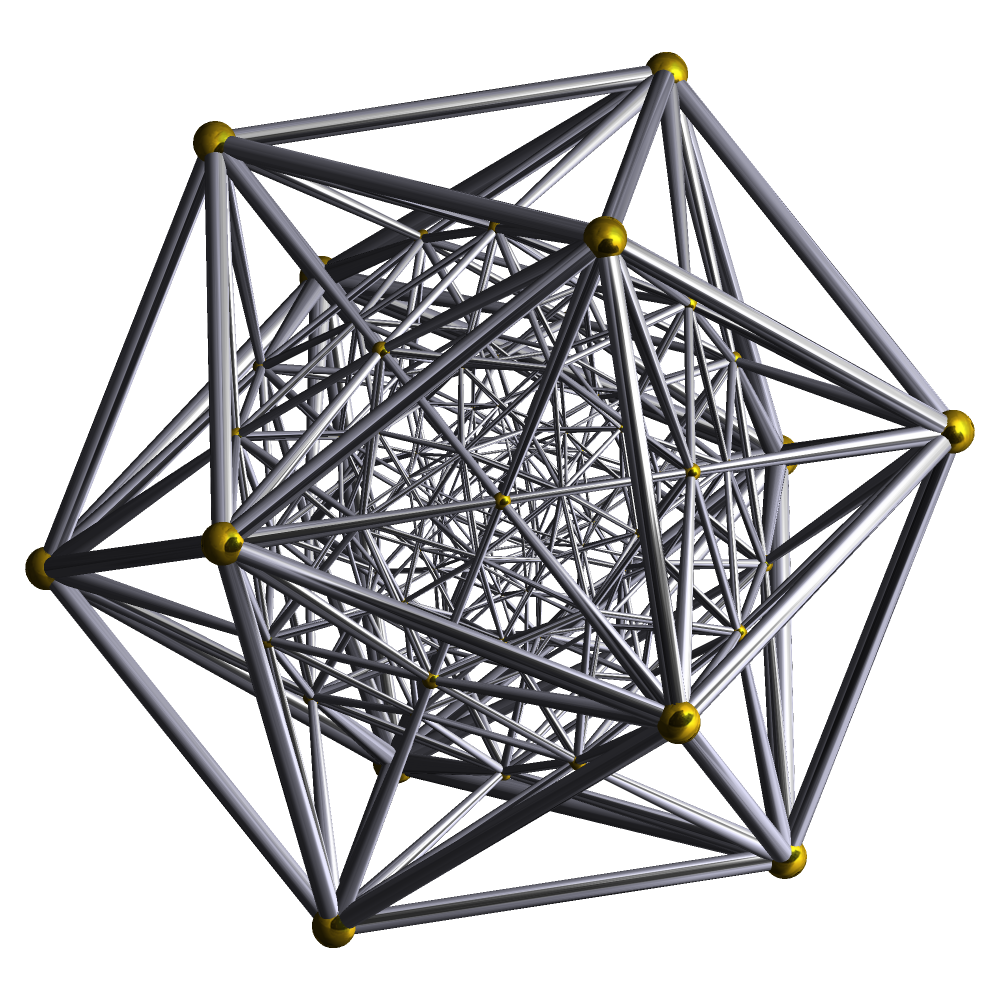
The elements of are quaternions of norm one, and it turns out that they are the vertices of a 4-dimensional regular polytope: a 4-dimensional cousin of the Platonic solids. It deserves to be called the ‘hypericosahedron’, but it is usually called the 600-cell, since it has 600 tetrahedral faces. Here is the 600-cell projected down to 3 dimensions, drawn using Robert Webb’s Stella software:
Explicitly, if we identify with , the elements of are the points
and those obtained from these by even permutations of the coordinates. Since these points are closed under multiplication, if we take integral linear combinations of them we get a subring of the quaternions:
Conway and Sloane [CS] call this the ring of icosians. The icosians are not a lattice in the quaternions: they are dense. However, any icosian is of the form where , and live in the golden field
Thus we can think of an icosian as an 8-tuple of rational numbers. Such 8-tuples form a lattice in 8 dimensions.
In fact we can put a norm on the icosians as follows. For the usual quaternionic norm has
for some rational numbers and , but we can define a new norm on by setting
With respect to this new norm, the icosians form a lattice that fits isometrically in 8-dimensional Euclidean space. And this is none other than !
Klein’s Icosahedral Function
Not only is the lattice hiding in the icosahedron; so is the Dynkin diagram. The space of all regular icosahedra of arbitrary size centered at the origin has a singularity, which corresponds to a degenerate special case: the icosahedron of zero size. If we resolve this singularity in a minimal way we get eight Riemann spheres, intersecting in a pattern described by the Dynkin diagram!
This remarkable story starts around 1884 with Felix Klein’s Lectures on the Icosahedron [Kl]. In this work he inscribed an icosahedron in the Riemann sphere, . He thus got the icosahedron’s symmetry group, , to act as conformal transformations of — indeed, rotations. He then found a rational function of one complex variable that is invariant under all these transformations. This function equals at the centers of the icosahedron’s faces, 1 at the midpoints of its edges, and at its vertices.
Here is Klein’s icosahedral function as drawn by Abdelaziz Nait Merzouk. The color shows its phase, while the contour lines show its magnitude:

We can think of Klein’s icosahedral function as a branched cover of the Riemann sphere by itself with 60 sheets:
Indeed, acts on , and the quotient space is isomorphic to again. The function gives an explicit formula for the quotient map .
Klein managed to reduce solving the quintic to the problem of solving the equation for . A modern exposition of this result is Shurman’s Geometry of the Quintic [Sh]. For a more high-powered approach, see the paper by Nash [N]. Unfortunately, neither of these treatments avoids complicated calculations. But our interest in Klein’s icosahedral function here does not come from its connection to the quintic: instead, we want to see its connection to .
For this we should actually construct Klein’s icosahedral function. To do this, recall that the Riemann sphere is the space of 1-dimensional linear subspaces of . Let us work directly with . While acts on , this comes from an action of this group’s double cover on . As we have seen, the rotational symmetry group of the icosahedron, , is double covered by the binary icosahedral group . To build an -invariant rational function on , we should thus look for -invariant homogeneous polynomials on .
It is easy to construct three such polynomials:
• , of degree , vanishing on the 1d subspaces corresponding to icosahedron vertices.
• , of degree , vanishing on the 1d subspaces corresponding to icosahedron edge midpoints.
• , of degree , vanishing on the 1d subspaces corresponding to icosahedron face centers.
Remember, we have embedded the icosahedron in , and each point in is a 1-dimensional subspace of , so each icosahedron vertex determines such a subspace, and there is a linear function on , unique up to a constant factor, that vanishes on this subspace. The icosahedron has vertices, so we get linear functions this way. Multiplying them gives , a homogeneous polynomial of degree on that vanishes on all the subspaces corresponding to icosahedron vertices! The same trick gives , which has degree because the icosahedron has edges, and , which has degree because the icosahedron has faces.
A bit of work is required to check that and are invariant under , instead of changing by constant factors under group transformations. Indeed, if we had copied this construction using a tetrahedron or octahedron, this would not be the case. For details, see Shurman’s book [Sh], which is free online, or van Hoboken’s nice thesis [VH].
Since both and have degree , is homogeneous of degree zero, so it defines a rational function . This function is invariant under because and are invariant under . Since vanishes at face centers of the icosahedron while vanishes at vertices, equals at face centers and at vertices. Finally, thanks to its invariance property, takes the same value at every edge center, so we can normalize or to make this value 1. Thus, has precisely the properties required of Klein’s icosahedral function!
The Appearance of E8
Now comes the really interesting part. Three polynomials on a 2-dimensional space must obey a relation, and , and obey a very pretty one, at least after we normalize them correctly:
We could guess this relation simply by noting that each term must have the same degree. Every -invariant polynomial on is a polynomial in and , and indeed
This complex surface is smooth except at , where it has a singularity. And hiding in this singularity is !
To see this, we need to ‘resolve’ the singularity. Roughly, this means that we find a smooth complex surface and an onto map
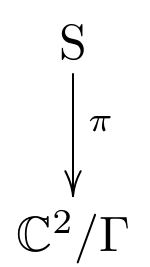
that is one-to-one away from the singularity. (More precisely, if is an algebraic variety with singular points , is a resolution of if is smooth, is proper, is dense in , and is an isomorphism between and . For more details see Lamotke’s book [L].)
There are many such resolutions, but one minimal resolution, meaning that all others factor uniquely through this one:
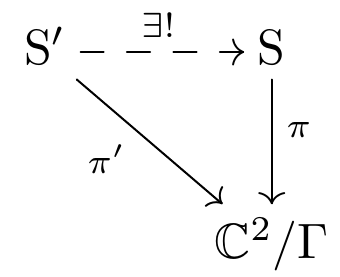
What sits above the singularity in this minimal resolution? Eight copies of the Riemann sphere , one for each dot here:
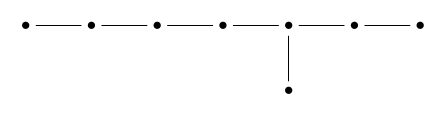
Two of these s intersect in a point if their dots are connected by an edge: otherwise they are disjoint.
This amazing fact was discovered by Patrick Du Val in 1934 [DV]. Why is it true? Alas, there is not enough room in the margin, or even in the entire blog article, to explain this. The books by Kirillov [Ki] and Lamotke [L] fill in the details. But here is a clue. The Dynkin diagram has ‘legs’ of lengths and :
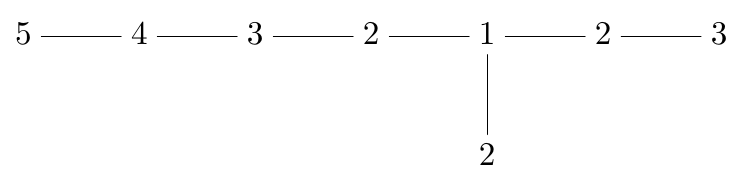
On the other hand,
where in terms of the rotational symmetries of the icosahedron:
• is a turn around some vertex of the icosahedron,
• is a turn around the center of an edge touching that vertex,
• is a turn around the center of a face touching that vertex,
and we must choose the sense of these rotations correctly to obtain . To get a presentation of the binary icosahedral group we drop one relation:
The dots in the Dynkin diagram correspond naturally to conjugacy classes in , not counting the conjugacy class of the central element . Each of these conjugacy classes, in turn, gives a copy of in the minimal resolution of .
Not only the Dynkin diagram, but also the lattice, can be found in the minimal resolution of . Topologically, this space is a 4-dimensional manifold. Its real second homology group is an 8-dimensional vector space with an inner product given by the intersection pairing. The integral second homology is a lattice in this vector space spanned by the 8 copies of we have just seen—and it is a copy of the lattice [KS].
But let us turn to a more basic question: what is like as a topological space? To tackle this, first note that we can identify a pair of complex numbers with a single quaternion, and this gives a homeomorphism
where we let act by right multiplication on . So, it suffices to understand .
Next, note that sitting inside are the points coming from the unit sphere in . These points form the 3-dimensional manifold , which is called the Poincaré homology 3-sphere [KS]. This is a wonderful thing in its own right: Poincaré discovered it as a counterexample to his guess that any compact 3-manifold with the same homology as a 3-sphere is actually diffeomorphic to the 3-sphere, and it is deeply connected to . But for our purposes, what matters is that we can think of this manifold in another way, since we have a diffeomorphism
The latter is just the space of all icosahedra inscribed in the unit sphere in 3d space, where we count two as the same if they differ by a rotational symmetry.
This is a nice description of the points of coming from points in the unit sphere of . But every quaternion lies in some sphere centered at the origin of , of possibly zero radius. It follows that is the space of all icosahedra centered at the origin of 3d space — of arbitrary size, including a degenerate icosahedron of zero size. This degenerate icosahedron is the singular point in . This is where is hiding.
Clearly much has been left unexplained in this brief account. Most of the missing details can be found in the references. But it remains unknown — at least to me — how the two constructions of from the icosahedron fit together in a unified picture.
Recall what we did. First we took the binary icosahedral group , took integer linear combinations of its elements, thought of these as forming a lattice in an 8-dimensional rational vector space with a natural norm, and discovered that this lattice is a copy of the lattice. Then we took , took its minimal resolution, and found that the integral 2nd homology of this space, equipped with its natural inner product, is a copy of the lattice. From the same ingredients we built the same lattice in two very different ways! How are these constructions connected? This puzzle deserves a nice solution.
Acknowledgements
I thank Tong Yang for inviting me to speak on this topic at the Annual General Meeting of the Hong Kong Mathematical Society on May 20, 2017, and Guowu Meng for hosting me at the HKUST while I prepared that talk. I also thank the many people, too numerous to accurately list, who have helped me understand these topics over the years.
Bibliography
[CS] J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices and Groups, Springer, Berlin, 2013.
[DV] P. du Val, On isolated singularities of surfaces which do not affect the conditions of adjunction, I, II and III, Proc. Camb. Phil. Soc. 30, 453–459, 460–465, 483–491.
[KS] R. Kirby and M. Scharlemann, Eight faces of the Poincaré homology 3-sphere, Usp. Mat. Nauk. 37 (1982), 139–159. Available at https://tinyurl.com/ybrn4pjq.
[Ki] A. Kirillov, Quiver Representations and Quiver Varieties, AMS, Providence, Rhode Island, 2016.
[Kl] F. Klein, Lectures on the Ikosahedron and the Solution of Equations of the Fifth Degree, Trüubner & Co., London, 1888. Available at https://archive.org/details/cu31924059413439.
[L] K. Lamotke, Regular Solids and Isolated Singularities, Vieweg & Sohn, Braunschweig, 1986.
[N] O. Nash, On Klein’s icosahedral solution of the quintic. Available as arXiv:1308.0955.
[Sh] J. Shurman, Geometry of the Quintic, Wiley, New York, 1997. Available at http://people.reed.edu/~jerry/Quintic/quintic.html.
[Sl] P. Slodowy, Platonic solids, Kleinian singularities, and Lie groups, in Algebraic Geometry, Lecture Notes in Mathematics 1008, Springer, Berlin, 1983, pp. 102–138.
[VH] J. van Hoboken, Platonic Solids, Binary Polyhedral Groups, Kleinian Singularities and Lie Algebras of Type A, D, E, Master’s Thesis, University of Amsterdam, 2002. Available at http://math.ucr.edu/home/baez/joris_van_hoboken_platonic.pdf.
[V] M. Viazovska, The sphere packing problem in dimension 8, Ann. Math. 185 (2017), 991–1015. Available at https://arxiv.org/abs/1603.04246.

Re: The Icosahedron and E8
I’ll be waiting eagerly! Your posts from back in the summer led me to poke around and find a few fun little things, but I never made progress on the central question.