The n-Category Café

There’s a fantastic expository paper that covers everything I’m about to say and much, much more:

Richard Gardner, The Brunn-Minkowski inequality. Bulletin of the American Mathematical Society 39 (2002), 355-405.

Thanks to Mark Meckes for mentioning this paper to me years ago. Cognoscenti like him may prefer this earlier, longer version. Both versions contain, among other things, a nice short proof of the inequality (Section 4 of the published version and Section 6 of the longer version). But I won’t give the proof here, nor will I mention the conditions for equality to hold.

The term $A + B$ is known as a Minkowski sum. You can think of $A + B$ as $A$ smeared out in a pattern dictated by $B$:

$$A + B = \bigcup_{b \in B} (A + b).$$

For instance, if $A$ is an egg shape (green) and $B$ is a quadrilateral (blue) then $A + B$ looks like the entire shape here:

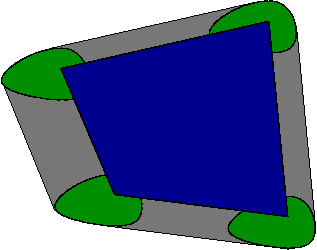
(When I wrote those words, I didn’t mean to invoke the mental image of smearing an egg around a table. But maybe it’s not such a bad image to have.) Or again, if $A$ is egg-like and $B$ is a line segment then $A + B$ looks like this:

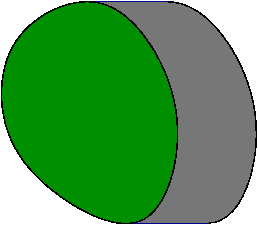
Of course, there’s also a complementary viewpoint: $A + B$ is $B$ smeared out in a pattern dictated by $A$:

$$A + B = \bigcup_{a \in A} (a + B).$$

In any case, an important observation is that

$A + B$ can have large volume even if $A$ and $B$ both have volume zero.

For instance, this happens in the plane when $A$ is a horizontal line segment and $B$ is a vertical line segment. There’s obviously no hope of getting an equation for $Vol(A + B)$ in terms of $Vol(A)$ and $Vol(B)$. But this example suggests that we might be able to get an inequality, stating that $Vol(A + B)$ is at least as big as some function of $Vol(A)$ and $Vol(B)$.

The Brunn-Minkowski inequality does this, but it’s really about linearized volume, $Vol^{1/n}$, rather than volume itself. If length is measured in metres then so is $Vol^{1/n}$. There’s also a much cruder corollary of Brunn-Minkowski that concerns actual volume. Take the Brunn-Minkowski inequality

$$Vol(A + B)^{1/n} \geq Vol(A)^{1/n} + Vol(B)^{1/n}$$

and raise each side to the power of $n$. The right-hand side can be expanded using the binomial theorem, and throwing away all except the first and last terms gives

$$Vol(A + B) \geq Vol(A) + Vol(B)$$

as a corollary of Brunn-Minkowski.

This is a much weaker statement than the Brunn-Minkowski inequality, because in deriving it we threw away a huge number of positive terms. But it’s interesting in its own right, and has an easy direct proof. Here’s an argument I was told by Joe Fu. I’ll indent it for easy skippability.

Let $A$ and $B$ be measurable subsets of $\mathbb{R}^n$, and assume they’re both bounded. (Once we’ve proved the bounded case, it’s not hard to deduced the general case, but I’ll leave that as a puzzle.) We’re going to prove that $A + B$ contains almost-disjoint translates of $A$ and of $B$, where by “almost disjoint” I mean that their intersection has measure zero. The inequality will follow.

The idea is that we shift $A$ as high as possible and $B$ as low as possible. Formally, define $h: \mathbb{R}^n \to \mathbb{R}$ by as $h(x_1, \ldots, x_n) = x_n$. (That’s $h$ for “height”, but any other nonzero linear functional would work just as well.) Choose $b^+ \in B$ maximizing $h(b^+)$ and $a^- \in A$ minimizing $h(a^-)$. It’s enough to show that

$$(A + b^+) \cap (a^- + B)$$

is a subset of a hyperplane, since then it has measure zero. So, let $x$ be any point in this intersection. We can write $x = a + b^+$ for some $a \in A$, and so

$$h(x) = h(a + b^+) = h(a) + h(b^+) \geq h(a^-) + h(b^+) = h(a^- + b^+).$$

But we can also write $x = a^- + b$ for some $b \in B$, and a similar argument gives $h(x) \leq h(a^- + b^+)$. So we’ve shown that every $x \in (A + b^+) \cap (a^- + B)$ belongs to the hyperplane $h^{-1}(h(a^- + b^+))$, and that completes the proof.

That was a very weak consequence of the Brunn-Minkowski inequality, but here’s a more powerful and interesting one. In a slogan:

Brunn-Minkowski for small balls is the isoperimetric inequality.

In other words, if you take any $A \subseteq \mathbb{R}^n$, and take $B$ to be a ball of radius tending to zero, then the Brunn-Minkowski inequality becomes the isoperimetric inequality in $\mathbb{R}^n$.

To explain this, I first need to explain what the isoperimetric inequality is. The word “isoperimetric” suggests the two-dimensional version: that among all subsets of $\mathbb{R}^2$ with a prescribed perimeter, the one with the greatest area is the disc. But I mean the general $n$-dimensional version, which I’ll now state.

Every reasonable subset $A \subseteq \mathbb{R}^n$ has a volume (its Lebesgue measure), which I’ll write now as $V_n(A)$. It also has a surface area, which I’ll write as $V_{n - 1}(A)$. The isoperimetric inequality states that for nice enough subsets $A \subseteq \mathbb{R}^n$ (and I’ll come back to what that means),

$$V_n(A) \leq V_n(r B^n)$$

where the radius $r$ is chosen so that

$$V_{n - 1}(A) = V_{n - 1}(r B^n).$$

We can easily solve for $r$ in this last equation, using the fact that $V_{n - 1}$ is homogeneous of degree $n - 1$. After a little bit of elementary algebraic rearranging, we find an equivalent form of the isoperimetric inequality that doesn’t have an “$r$” in it:

$$\frac{V_n(A)^{1/n}}{V_{n - 1}(A)^{1/(n -1)}} \leq \frac{V_n(B^n)^{1/n}}{V_{n - 1}(B^n)^{1/(n - 1)}}$$

for all $A \subseteq \mathbb{R}^n$.

This can be understood as follows.

Loosely speaking, the isoperimetric inequality says that the ratio of a shape’s volume to its surface area is greatest for balls. But we shouldn’t take the word “ratio” literally: for if we simply divided volume by surface area then we’d get a quantity measured in metres, so we could make it bigger simply by scaling the set up! What we want this ratio to be is a dimensionless quantity.

Since volume is measured in metres${}^n$ and surface area is measured in metres${}^{n - 1}$, we can get a dimensionless quantity by linearizing both things before we take the ratio. In other words, take the $n$th root of the volume and the $(n - 1)$th root of surface area, so that both are measured in metres. Then the ratio will come out to be dimensionless.

(If you’re feeling perverse, you could instead take the $(17/n)$th power of the volume and the $(17/(n - 1))$th power of the surface area, then divide one by the other. This would be a dimensionless quantity. But since it’s just the 17th power of the ratio in the last paragraph, and taking the 17th power is an order-preserving operation, it wouldn’t change the meaning of the inequality.)

To get much further, we need to ask: what is surface area? The usual idea is that the volume of a thin shell around $A$, of thickness $\varepsilon \approx 0$, should be approximately $\varepsilon$ times the surface area. So, we define

$$V_{n - 1}(A) = \lim_{\varepsilon \to 0+} \frac{V_n(A_\varepsilon) - V_n(A)}{\varepsilon},$$

where $A_\varepsilon$ means the set of all points within distance $\varepsilon$ of $A$. Since we’re talking about Minkowski sums, it’s useful to observe that

$$A_\varepsilon = A + \varepsilon B^n$$

where $B^n$ means the $n$-dimensional unit ball.

I confess that I don’t know exactly when the limit above exists; I guess there are measurable sets $A$ for which it doesn’t. And among those sets for which the limit does exist, I don’t know when it’s the right definition of surface area. But certainly everything works as it should when $A$ is convex and compact, since then $V_n(A_\varepsilon)$ is actually a polynomial in $\varepsilon$ whose linear term is the surface area. (That’s part of Steiner’s theorem.) So let’s just assume that $A$ is convex and compact.

Now we’ll use this formula to calculate the surface area of the unit ball. Taking $A = B^n$,

$$\begin{aligned} V_{n - 1}(B^n) & = \lim_{\varepsilon \to 0} \frac{V_n((1 + \varepsilon)B^n) - V_n(B^n)}{\varepsilon} \\ & = V_n(B^n) \cdot \lim_{\varepsilon \to 0} \frac{(1 + \varepsilon)^n - 1}{\varepsilon} \\ & = n V_n(B^n), \end{aligned}$$

using the fact that $V_n$ is homogeneous of degree $n$. So,

$$V_{n - 1}(B^n) = n V_n(B^n).$$

For instance, in $\mathbb{R}^3$, the volume of the unit ball is $(4/3) \pi$ and the surface area of the unit sphere is $3 \cdot (4/3) \pi = 4\pi$.

Back to Brunn-Minkowski! I promised to show you that the isoperimetric inequality is just the Brunn-Minkowski inequality in the case where one of the two sets involved is a small ball. We’ve put the isoperimetric inequality into a form where it involves $(1/n)$th powers, which also appear in the Brunn-Minkowski inequality. So things are looking promising… Here goes.

Take $A \subseteq \mathbb{R}^n$ (definitely measurable, probably convex and compact). The Brunn-Minkowski inequality tells us that for all $\varepsilon \gt 0$,

$$V_n(A + \varepsilon B^n)^{1/n} \geq V_n(A)^{1/n} + V_n(\varepsilon B^n)^{1/n}.$$

Rearranging, this is equivalent to

$$\frac{V_n(A + \varepsilon B^n) - V_n(A)}{\varepsilon} \geq \frac{(V_n(A)^{1/n} + \varepsilon V_n(B^n)^{1/n})^n - V_n(A)}{\varepsilon}.$$

Now let $\varepsilon \to 0$. The left-hand side is just the definition of $V_{n - 1}(A)$. The right-hand side is recognizable as a derivative, give or take a constant factor. So the Brunn-Minkowski inequality for (vanishingly) small balls states that for nice enough $A \subseteq \mathbb{R}^n$,

$$V_{n - 1}(A) \geq n V_n(A)^{(n - 1)/n} V_n(B^n)^{1/n}.$$

This looks like a mess until we remember the formula for the surface area of the unit ball: $V_{n - 1}(B^n) = n V_n(B^n)$. Using this to get rid of the $n$ in the inequality, and doing one last bit of elementary rearrangement, we get

$$\frac{V_n(A)^{1/n}}{V_{n - 1}(A)^{1/(n -1)}} \leq \frac{V_n(B^n)^{1/n}}{V_{n - 1}(B^n)^{1/(n - 1)}}.$$

And that’s exactly the isoperimetric inequality.