The n-Category Café

Cubism

As described in The first Edge of the Cube, connections are conveniently conceived in terms of their parallel transport functor.

Given such a transport functor, there are various natural things one can do with it, like locally trivializing it (this takes us along a first edge of a cube of concepts), or categorifying it or quantizing it (by which we proceed along other edges of this cube).

Yet another edge of The Cube: Differentiation

For practical purposes of somewhat more urgent relevance, however, is yet another operation: locally trivializing and differentiating the transport functor – which is a morphism of Lie $n$-groupoids satisfying certain conditions – to obtain a morphism of Lie $n$-algebras satisfying certain conditions.

Interlude: Curvature

The appearance of the inner automorphisms and inner derivations here is due to the fact that the Lie algebra morphisms on the right really are the differentials of pseudofunctors from the pair groupoid of $X$. That’s because the tangent algebroid $\mathrm{Vect}(X)$ is the 1-algebroid obtained from differentiating the pair groupoid $$\mathrm{Vect}(X) := \mathrm{Lie}(X \times X) \,.$$ But locally, say for $X$ convex, a pseudofunctor on the pair groupoid is essentially the same as an $n$-functor on the fundamental $n$-groupoid $\Pi_n(X)$. But these describe flat $n$-transport.

As a result, the morphisms here don’t just describe the parallel $n$-transport, but actually the corresponding $n$-curvature. And that, as described in part in

$n$-Curvature

is an $(n+1)$-functor which takes values in inner automorphisms of the structure group. One way to understand this is by pairing Schreier theory of groupoid extensions with the Atiyah sequence of groupoids associated with principal bundles. This observation goes back to Danny Stevenson. I discussed it in $n$-Transport and Higher Schreier Theory.

So

A connection with values in a Lie $n$-algebra $g_{(n)}$ is not, in general, a morphism $$\mathrm{Vect}(X) \to g_{(n)}$$ (only if all its $k$-form curvatures vanish), rather, it is a morphism $$\mathrm{Vect}(X) \to \mathrm{inn}(g_{(n)})$$ to the Lie $(n+1)$-algebra of inner derivations of $g_{(n)}$.

This actually proves to clarify a lot of things that otherwise remain mysterious or require awkward workarounds.

In a sense

Curvature is more fundamental than connection.

Since Lie $n$-algebras may be tricky to integrate to Lie $n$-groups, it would be very useful to have a notion of connection with values in a Lie $n$-algebra which doesn’t require making the integrated parallel transport manifest, but realizing just its differential part, which takes values just in the Lie $n$-algebra.

This is to some degree complementary to the approach by Anders Kock: where Kock uses synthetic differential geometry, this here is supposed to use ordinary differential goemetry.

Descent at the Lie level: how to do it right

I had begun thinking about the issue of putting the right gluing data/descent conditions on (dual) morphisms of qDGCAs $$f^* : (\wedge^\bullet sg_{(n)}^*, d_{\mathrm{inn}(g_{(n)})}) \to \Omega^\bullet(X)$$ here, by trying to formulate the right descent condition for arbitrary covers of base space. But this has the problem that the linearization in general misses crucial data.

But then from Jim Stasheff I learned what is the right way to do this:

A) Don’t consider connection forms on arbitrary covers, but restrict attention to the cover given by the total space of the bundle itself. (This avoids the above problem.)

B) Pass to the differentiated version of the usual statement of the Cartan-Ehresmann conditions on a connection 1-form. This makes their true nature manifest: these two conditions really say that the connection commutes with certain derivations.

The program

Thinking about this for a while, it turns out that there is a nice story to be told here. It deserves to be an edge of the cube by itself. So now the cube is spanned by four edges. The projection to three dimensions of relevance for the present case is this:

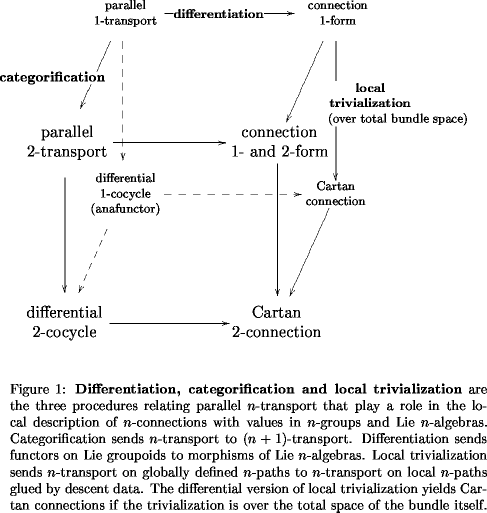
With Jim I am trying to go all the way along the main diagonal and formulate, for any Lie $n$-algebra $g_{(n)}$ the theory of $n$-Cartan-Ehresmann connections with values in $g_{(n)}$. This is the goal of

U.S. & J. Stasheff
$\;\;$ Structure of Lie $n$-Algebras
$\;\;$ Connections with Values in Lie $n$-Algebras
$\;\;$ Zoo of Lie $n$-Algebras

aspects of which I had mentioned before (I, II, III, IV).

Interlude: Ehresmann versus Cartan.

I am saying “Cartan-Ehresmann connection” where, strictly speaking, I mean “Ehresmann connection”:

a Lie algebra valued 1-form $A \in \Omega^1(P,g)$ on the total space of a principal $G$-bundle $P$ satisfying two compatibility conditions.

If we understand that, we’ll easily understand the Cartan version, too, which is about G-bundles whose structure group may be reduced. Derek Wise in Gravity and Cartan Geometry gives a nice description of the two concepts and their relation.

What Cartan-Ehresmann really means: differentiating the Universal Transition

When trying to understand what statements made in terms of differential forms really mean, it is usually helpful to find the corresponding integrated statements.

In a way, this is the very motivation of the synthetic differential geometry approach of Lawvere, Kock, and others: reformulate differential geometry in a way that tangent vectors literally appear like little paths.

Anyway: what do the Ehresmann conditions on a connection 1-form on the total space of a principal bundle correspond to when integrated?

John Baez and Derek Wise emphasized the nice geometric picture behind it (TWF 243).

That’s cool. But here we need the “arrow-theoretic” meaning of Cartan-Ehresmann. It should be this:

In

U.S. & Konrad Waldorf
Parallel Transport and Functors
arXiv:0705.0452v1 [math.DG]

we describe in detail how the local trivialization of a parallel transport functor gives rise to a functor on paths of the cover, which extends to a functor on the Universal Transition (called the “path puhsout” in that paper).

This universal transition $$C(Y)$$ is a groupoid whose morphisms consist of

- paths in the cover $Y$

- jumps between patches

such that the obvious compatibility condition is satisfied. The corresponding functor $$C(Y) \to \Sigma G$$ is actually the smooth anafunctor corresponding to the local trivialization of the parallel transport.

In a sense we have

A Cartan-Ehresmann connection is the differential of this anafunctor.

To make this morally true statement precisely true, we need to follow Jim Stasheff’s advice and locally trivialize the bundle not over an arbitrary cover – but over itself.

The crucial step: Canonically trivialize the bundle over itself

Every principal $G$-bundle $p : P \to X$ canonically trivializes when pulled back to its own total space $P$ $$P \times_X P \simeq P \times G \,.$$ Fix this canonicaly trivialization and then turn the crank on the universal transition anafunctor described above. One finds that our anafunctor now will be such that

- It sends jumps between patches – which now are labeled by group elements $g \in G$ – to precisely that group element. This is the integrated version of the first Cartan-Ehresmann condition.

- It sends paths $\gamma \cdot g$ that arise from translation with $g \in G$ to the image of the original path $\gamma$, conjugated by $g$. This is the integrated version of the second Cartan-Ehresmann condition.

Arrow theory and Implementation

Of course there are much more pedestrian ways to understand the Cartan-Ehresmann condition from the point of view of locally trivialized bundles with connection. We give a detailed description of a bunch of elementary but useful facts concerning this in section 3.3.2 of Connections with Values in Lie $n$-algebras.

The real point of the above exercise is the following:

- On the one hand we discover the arrow theory that underlies the concept of a Cartan-Ehresmann connection. While for ordinary bundles the above functorial description may feel like overkill, its great advantage is that once we have understood this, we easily understand its generalization to $n$-bundles with connection.

- On the other hand, as the above table indicates, we see how the arrow theory implements into the world of quasi-free differential graded algebras. That’s good, because while arrow-theory is useful for understanding what’s going on, implementation in qDGCAs allows us to efficiently compute.

In particular, we see that, on the qDGCA level, the consistency conditions on our connection are a bunch of commutator relations. That’s very handy.

But here there is actually also a good arrow-theoretic way to understand these commutators as intertwiners of arrow-theoretic Lie derivatives.

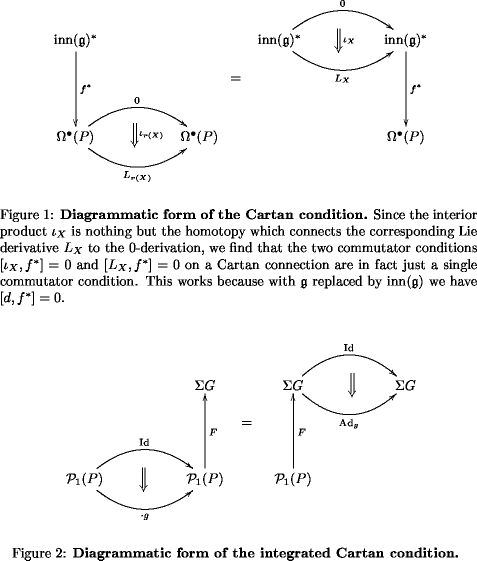
This will be useful when passing from 1-connections to $n$-connections.