Musings

My daughter entered fifth grade last week and, in her school, that means that she and her classmates were each issued a Dell Latitude laptop. They use them in school and then take them home and use them in preparing their homework as well.

Overall, I’m very pleased with the school laptop program. There are so many educational resources the kids can tap into. Tonight, her homework assignment involved looking up aurochs and woolly mammoths and other extinct large mammals. Even minor things, like her still-dodgy spelling, have shown marked improvement, thanks to the shear repetition of warnings from the spell-checker. On the other hand, there is something eery about watching a 10-year old give a PowerPoint presentation.

There was one thing, however, that I really dreaded: figuring out how to add her Windows laptop to our home network.

Last time I had to do that (for a guest’s Windows ME machine, which is to say it’s been a while), entailed hours of frustration. I never did succeed in getting the wireless card to associate with our closed network and getting past the %$#@ “Wizard”s to configure the ethernet interface with a static IP address was a major pain.

Anyway, this time things went quite a bit more smoothly.

1. Her computer teacher happily supplied me with the MAC address of the wireless card.
2. This time, the card had no trouble associating with a closed network; all I had to do was type in the SSID.
3. After some emails back and forth, the teacher granted Admin privileges on the laptop and I was able to configure this wireless interface with a static IP address.
4. Setting up the laptop to use our laser printer was slightly less obvious. This page from Microsoft is a complete lie. Microsoft discontinued AppleTalk support in Windows XP (it was there in Windows 2000). The solution was to turn on Printer Sharing on one of our existing computers, and then direct her machine to print to

   http://192.168.x.x:631/printers/PRINT_QUEUE

   (a remote IPP printer).

So far, “supporting” this Windows machine been relatively painless. I’m keeping my fingers crossed.

The same week saw another change in our home network. After over a decade of trouble-free service, our gateway router (a dual-ethernet Power Computing PowerCenter Pro, with a 400 MHz G3 card, running MacOS 9.2 and IPNetRouter) coughed and sputtered and decided that it needed to start enjoying an active adult lifestyle.

Off I went to Frys and returned with a discounted Belkin F5D7231-4. It’s about as full-featured a router as one could imagine, with Appletalk-bridging, a stateful firewall, inbound port mapping, … The only feature I miss¹ is DNS-forwarding.

I don’t miss the whir of the three fans in the PCP, though.

For somewhat obscure reasons, I’ve been looking, recently, at a recent paper by Aharony, Clark and Karch. They consider the following problem. Say we have two CFT’s, $C_1$, and $C_2$. each of which has an AdS dual description. Each CFT has its own conserved, traceless, stress tensor. The AdS dual of $C_1\times C_2$ is the disjoint union of the corresponding AdS spaces. (Aharony et al use the phrase “direct sum” instead of “disjoint union”, but one learns to make allowances …) The graviton, on each component of this disjoint union, couples in the usual way to the stress tensor of the corresponding boundary theory.

But now suppose we deform the theory by choosing a pair of relevant operators, $O_1$, $O_2$, (with scaling dimensions $\Delta_1$ and $\Delta_2=d-\Delta_1$) in the two theories and adding

(More generally, it’s interesting to contemplate a marginal or relevant perturbation of the erstwhile decoupled theory.)

What is the AdS dual of the deformed theory?

Obviously, by turning on $\Delta S$, we are correlating the boundary conditions of the fields on the two formerly disjoint AdS spaces. So we should think of these two spaces as glued together at their common boundary. In the boundary field theory, we no longer have two seaparately conserved stress tensors. The total stress tensor, $$T = T_1 + T_2$$ is conserved, but $$\tensor{\tilde{T}}{_\mu_\nu} = c_2 T^{(1)}_{\mu\nu} - c_1 T^{(2)}_{\mu\nu} + \epsilon \tfrac{(c_1 \Delta_2-c_2\Delta_1)}{d}\eta_{\mu\nu} O_1 O_2$$ is not. Here $c$, defined by $$\langle T_{\mu\nu}(0) T_{\rho\sigma}(x) \rangle = \frac{c}{|x|^4} \left(\eta_{\mu\rho}\eta_{\nu\sigma} + \eta_{\mu\sigma}\eta_{\nu\rho} -\tfrac{2}{d} \eta_{\mu\nu}\eta_{\rho\sigma}\right)$$ is one measure of the central charge of the conformal field theory. Instead of being conserved, to leading order in $\epsilon$, $$\partial^\mu \tensor{\tilde{T}}{_\mu_\nu} = K_\nu = \epsilon\tfrac{(c_1+c_2)}{d} \left(\Delta_2 (\partial_\nu O_1)O_2 - \Delta_1 O_1(\partial_\nu O_2)\right)$$

Correspondingly, the modes of the bulk graviton which couple to $\tensor{\tilde{T}}{_\mu_\nu}$ must pick up a mass via the Higgs mechanism (swallowing the bulk vector field which couples to $K_\nu$). The graviton mass is related, in the standard way, to the anomalous dimension of $\tensor{\tilde{T}}{_\mu_\nu}$, $$m^2_{\text{grav}} = d (\Delta_{\tensor{\tilde{T}}{_\mu_\nu}} -d) = \epsilon^2 \left(\frac{1}{c_1}+\frac{1}{c_2}\right)\frac{\Delta_1 \Delta_2 d}{(d+2)(d-1)}$$

Rather prettily, a bulk calculation of the effect of the deformed boundary conditions yields an identical expression for the mass of these graviton modes. Note that it is a feature of AdS space, unlike (say) Minkowski space, that the graviton can smoothly acquire a mass.

The authors then turn to some speculations as to which theories have AdS duals (either as a single AdS space, or a set of disjoint spaces glued along their boundaries). I’m not particularly happy with their proposal. Indeed, I think that any QFT which is controlled by a nontrivial UV fixed point should have some sort of AdS dual. This description is, however, unlikely to be a useful one unless there’s some sort of large-$N$ limit which makes the bulk theory semiclassical.

The possibility that there may exist, at certain points in the moduli space of such theories, multiple conserved spin-2 currents, does not seem — in any robust way — to be correlated with the number of factors in the gauge group¹.

Still, it’s a very interesting question to contemplate , and I would try to phrase the answer in terms of the topology of the space of boundary fields.

Seed Magazine may have more bloggers; they have a magazine to flog. But if you want the very best in physics blogging, we’ve got you covered here on golem. Introducing

The authors are: mathematical physicist and über-blogger-before-anyone-heard-of-blogging, John Baez, philosopher of Mathematics and blogger, David Corfield, and our very own Urs Schreiber, the mainstay of the String Coffee Table

They should be doing some fascinating stuff on the interface between physics and mathematics. So drop by, or follow the action on Planet Musings.

Speaking of the String Coffee Table, since Urs will probably carry his n-categorical thoughts over to the new blog, it might be time to solicit some new members to the SCT, renewing the focus on all facets of string theory and high energy physics. Contact me privately, if you’re interested in getting involved.

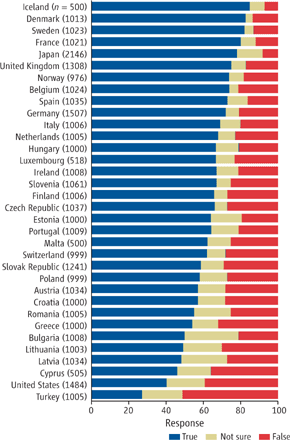
Public opinion on Evolution by country

Well, at least we beat Turkey!

[Via livescience], a comparative study of beliefs about evolution in 34 countries. Were it not for the Turks, the US would have finished dead last.

The authors of the study found the usual suspects — the peculiar American brand of Protestant Fundamentalism, with its emphasis on biblical literalism, and the use of creationism as a political wedge-issue by the Right — as largely responsible for the difference between the US and other countries. (In the US, there were significant correlations between self-description as “conservative”, opposition to abortion and disbelief in evolution. Not so in Europe.)

More hopeful, at least to me, was simple knowledge of modern genetics as a predictor:

Third, genetic literacy has a moderate positive relationship to the acceptance of evolution in both the United States and the nine European countries. This result indicates that those adults who have acquired some understanding of modern genetics are more likely to hold positive attitudes toward evolution. The total effect of genetic literacy on the acceptance of evolution was similar in the United States and the nine European countries.

Although the mean score on the Index of Genetic Literacy was slightly higher in the United States than the nine European countries combined, results from another 2005 U.S. study show that substantial numbers of American adults are confused about some of the core ideas related to 20th- and 21st-century biology. When presented with a description of natural selection that omits the word evolution, 78% of adults agreed to a description of the evolution of plants and animals (see table S2 in SOM). But, 62% of adults in the same study believed that God created humans as whole persons without any evolutionary development.

It appears that many of these adults have adopted a human exceptionalism perspective. Elements of this perspective can be seen in the way that many adults try to integrate modern genetics into their understanding of life. For example, only a third of American adults agree that more than half of human genes are identical to those of mice and only 38% of adults recognize that humans have more than half of their genes in common with chimpanzees. In other studies (1, 14, 15), fewer than half of American adults can provide a minimal definition of DNA. Thus, it is not surprising that nearly half of the respondents in 2005 were not sure about the proportion of human genes that overlap with mice or chimpanzees.

It would be amusing to cross-correlate these results with those international surveys of test scores in math and science. One’s cursory impression is that the same countries rank near the top (and near the bottom) of both data sets. That Johnny doesn’t know what DNA is is probably not unrelated to the fact that he can’t do simple algebra either.

This blog uses SVG for figures, wherever possible. If you have difficulty reading the text, you can bump up the font size in your browser, and the equations and the figures scale up smoothly too. The labels in the figures are actual text, which makes the SVG searchable, and — at least in principle — accessible to the blind.

Unfortunately, for an increasing fraction of my readers, the text in the figures is completely spooged. What they see is the result of the native SVG renderer (in Mozilla/Firefox, Opera or WebKit) substituting some default font for the embedded font in the figures. In running text, substituting fonts mostly produces acceptable results. In figures, where precise placement and font metrics are crucial, the result is almost always a disaster.

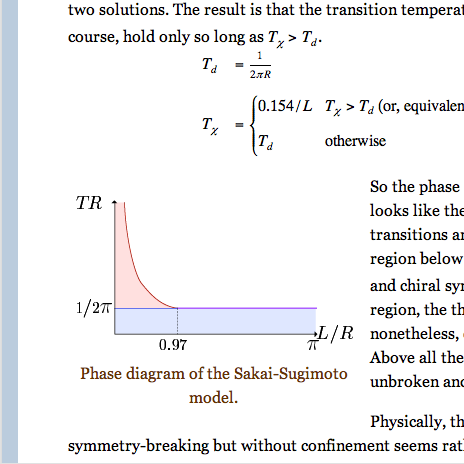
An SVG figure, rendered using Adobe’s plugin.

That’s why Adobe Illustrator embeds the fonts (subsetted to just the glyphs used) using CSS2 Font Descriptions. The Adobe SVGViewer plugin supports this, as you can see above. The other renderers, however, do not.

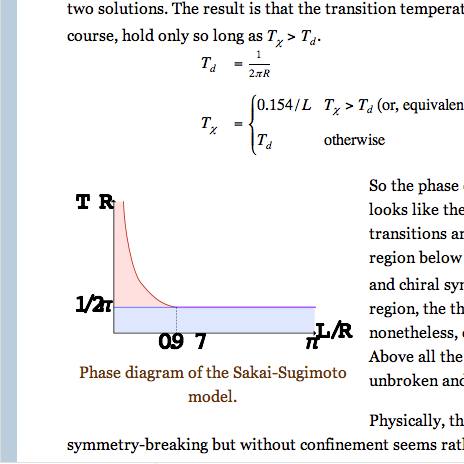
The same figure, rendered using Mozilla’s native SVG renderer.

Once upon a time, I could assume that anyone, who could see the SVG figure at all¹, was seeing it with the Adobe plugin. No longer. Firefox and Opera have their native SVG renderer enabled by default. So will the next version of Safari. Increasingly, viewers are seeing the broken version of the figure, instead of the expected one.

The absence of support for (any form of) font embedding is a bug in Mozilla. I consulted with my guru in such matters, Henri Sivonen, and it’s pretty clear that font embedding is not going to get implemented anytime soon, if ever.

The only rational choice, alas, is to give up on text being text, and convert all fonts in the SVG figures to outlines.

In Adobe Illustrator, after preparing the figure, one

1. does a Select→All, and then Type→Create Outlines.
2. opens the SVG file in a text editor and changes

   width="NNN" height="NNN"

   to

   width="100%" height="100%"

   to deal with this bug.

I’ve “fixed” the figure in my most recent post. As time permits, I’ll go back and “fix” the figures in my older posts as well.

There was a beautiful talk on Friday by David Sahakyan about his work with Parnachev on the Sakai-Sugimoto model (and the contemporaneous, but somewhat more extensive work by Aharony, Sonnenschein and Yankielowicz). This is the most QCD-like of all the AdS/CFT backgrounds (in a certain limit, it is QCD with massless quarks) and it exhibits both confinement and $U(N_f)\times U(N_f)\to U(N_f)_{\text{diag}}$ chiral symmetry breaking.So I thought it would be nice to give a little review.

Sign seen in the window of a New York dry cleaner:

Your clothes can be tested for shatnes by the Shatnes Laboratory

203 Lee Avenue, Brooklyn

I’m thinking, “What a great application of mass spectroscopy!” You?

As you can probably tell, I’m really rather enamoured of the application of AdS/CFT technology to study the properties of the quark-gluon plasma at RHIC (I, II, III). A lot of nuclear physicists (who are used to making various crude approximations in attempting to describe nuclear dynamics) are also quite excited.

In the AdS/CFT approach, one replaces finite-temperature QCD (in a strongly-coupled plasma phase) with some other (usually supersymmetric) gauge theory which, unlike QCD, is controlled by a nontrivial UV fixed point. So the microscopic degrees of freedom in the plasma are rather different from those of QCD. Moreover, calculations are done at large-$N_c$ and large $\lambda=g^2 N_c$ limit, whereas we are really interested in $N_c=3$, $\lambda\sim 20$. Still, if we are interested in hydrodynamic and finite-temperature transport properties, the precise microscopic degrees of freedom may not matter too much. And one can astutely study ratios of quantities in which one might expect the number of microscopic degrees of freedom to drop out. Moreover, one can test the robustness of the result by computing in different theories ($\mathcal{N}=4,\, \mathcal{N}=2^*,\dots$).

Still, one might be sceptical of the whole approach, were there some other approach to calculating transport coefficients in a strongly-coupled quark-gluon plasma. Unfortunately, for these purposes, AdS/CFT is the only game in town.

A plot of $f(v,\theta)$, showing both the mild dependence on $v$ and on $\theta$. The upper curve is for $\theta=\pi/2$; the lower curve is for $\theta=0$, with the behaviour for general $\theta$ interpolating between the two.

With that preamble, I thought I’d point to some of the latest interesting results in the subject. One important effect observed at RHIC is the suppression of J/Ψ production. The intuitive picture is that, when $c\overline{c}$ pair is produced in the collision, instead of forming a $c\overline{c}$ bound state, the potential between them is screened and, instead, they tend to form charmed mesons. The static heavy-quark potential is well-understood from lattice studies. And so are the corrections due to finite-temperature effects.

Unfortunately, the lattice calculations don’t tell the whole story, as they apply to static quarks, whereas the $c\overline{c}$ pairs at RHIC are produced with significant velocity, relative to the plasma. Experimentally, this appears to be important. So it’s interesting to study the velocity dependence of the screening length theoretically. Which is where AdS/CFT comes in.

Liu, Rajagopol and Wiedemann studied the problem in the $\mathcal{N}=4$ theory, where they obtained $$L_s(v,T) = \frac{f(v,\theta)}{\pi T} (1-v^2)^{1/4}$$ where $f(v,\theta)$ is a function that depends very mildly on the velocity of the $q\overline{q}$ dipole relative to the plasma and on its orientation, $\theta$, relative to its velocity.

$L_s(0,T)$ is off by about a factor of 2 from the lattice QCD results ($L_s\sim 0.5/T$ for 2 flavours of light quarks, and $L_s\sim 0.7/T$ without dynamical quarks). But that’s not an unexpected discrepancy, given the arguments above. What’s important (and, one hopes, more robust) is the velocity dependence $$L_s(v,T) \sim L_s(0,T) (1-v^2)^\xi$$ where, for the $\mathcal{N}=4$ theory, one has $\xi=1/4$.

Càceres, Natsuume and Okamura studied a series of other backgrounds, and argue that $\xi=1/4$ for conformal theories but that, systematically, $\xi\lt 1/4$ for non-conformal theories, like the Klebanov-Tseytlin cascade. Based on their examples, they conjecture a formula $$\xi = \tfrac{1}{4}- \tfrac{3}{16}\left(1-3c_s^2\right)$$ relating the exponent to the sound speed in the plasma. If such a relation holds, one would obtain $\xi\sim 0.22$ for the quark gluon plasma at RHIC.