In week294 of This Week’s Finds, hear an account of Gelfand’s famous math seminar in Moscow. Read what Jan Willems thinks about control theory and bond graphs. Learn the proof of Tellegen’s theorem. Meet some categories where the morphisms are circuits, and learn why a category object in Vect is just a 2-term chain complex. Finally, gaze at Saturn’s rings edge-on:
TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2194
Interesting point. I was just trying to keep things simple. For me the meshes in week293 were just a formal trick for re-expressing Kirchoff’s current law
as an exactness condition
in charming analogy to how Kirchoff’s voltage law
follows from
And I wanted to do this in as bland a way as possible. You’re right, we could add more meshes and get some 2nd homology and cohomology, without ruining exactness in degree 1. But that would make the meshes ‘interesting’, whereas my goal was to have them be clearly ‘just a formal trick’.
But there are real electrical engineers who really use mesh currents — so I guess we should see what they do!
I think the ‘essential mesh’ idea, explained at the above link, amounts to taking a connected planar graph and adding just enough meshes to obtain a contractible 3-term chain complex.
The question popped up quite urgently for me as I was using your presentation as a bit of a moral guidance for writing a chapter in a book I’m working on with Gunnar Carlsson and Andrew Blumberg on Topological Data Analysis: we’re touching on homology/cohomology for understanding electrical circuits as part of the introductory text sketching out why topology could be relevant in the first place.
In my exposition, I’m introducing all meshes, and using exactness in the first degree, because I couldn’t figure out why on earth not. If you DO figure out what the people who do use mesh currents actually do, I’d appreciate to learn!
I’m glad you’re including this material in an introductory text; it’s fun stuff.
The Wikipedia article on mesh analysis is not too bad for starters. But here’s one practical reason for introducing these ‘mesh currents’. If we want to keep track of the current in the naive way, we need a number for each edge of our graph.
Unfortunately, these numbers aren’t independent: they satisfy equations coming from Kirchoff’s current law. The number of independent currents is not the number of edges in our graph: it’s the dimension of the 1st homology of our graph.
This is a hassle! We can use fewer numbers if we introduce mesh currents and let . Then Kirchhoff’s current law will hold automatically.
And if we do what I said — introduce only enough meshes to kill the 2nd homology — the numbers , one for each mesh , will be the shortest possible list of numbers that we can use to describe an arbitrary solution of Kirchhoff’s current law.
In other words: in this case the meshes give a basis for the 1st homology of our graph.
But if we do what you said — introduce as many meshes as possible — you’ll need more mesh currents. The 1st homology will be a nontrivial quotient of the space of mesh currents.
There should be something about syzygies going on here. You seem to be on your way to constructing a resolution of the original 2-term chain complex! That’s not efficient for what we’re doing here, but it could be interesting in some other way. And certainly students deserve more intuitive introductions to the concept of ‘resolution’.
By the way — you might enjoy this section of a paper by Jan Willems. It’s about polynomial modules and syzygies in electrical engineering!
I wrote:
Let’s compute the power using Kirchoff’s voltage law and Kirchoff’s current law:
Hey — it’s zero!
At first this might seem strange. The power is always zero???
But maybe it isn’t so strange if you think about it: it’s a version of conservation of energy. In particular, it fails when we consider circuits with current flowing in from outside: then δI doesn’t need to be zero. We don’t expect energy conservation in its naive form to hold in that case. Instead, we expect a "power balance equation", as explained in "week290".
But maybe it is strange. After all, if you have a circuit built from resistors, why should it conserve energy? Didn’t I say resistors were dissipative?
I still don’t understand this as well as I’d like. The math seems completely trivial to me, but its meaning for circuits still doesn’t seem obvious. Can someone explain it in plain English?
I think it’s easier to understand if you just consider a circular loop of resistors and compute the power dissipated by current flowing around, using
The power totals to zero because ‘what goes up must come down’: as much current is flowing to regions of higher potential φ as is flowing to regions of lower potential.
It’s sort of like how you can’t actually get power by having water flow around in a loop, powering a waterwheel as in that picture by Escher….
That’s me down at the bottom, trying to figure it out. I think I got mixed up because I mistakenly wanted to use
and imagined current flowing around with nonzero and . Do y’all see why this is wrong?
I seem to remember you orienting your wires, for one thing; put another way, “power” isn’t “Power”.
I’m also trying to think of means to setting up such a nonconstant voltage on your circuit; the only thing that comes to mind is standing each node on a variable battery, the other ends of these joined to a common short via a nullator… are there norators hiding somewhere?
The discussion on Tellegen’s theorem motivated me to write up some stuff that I’ve had on my mind for a while. It is about what I call “Cut functions”.
(Know a better name?) These functions tell you the power that flows between subcircuits, that you “cut” from the total circuit.
So the cut function of a vertex-edge pair is just V*I. It measures the power leaving the subcircuit through that edge. The derivaton of this uses the same logic as Tellegen’s theorem, and Tellegen’s theorem follows from it. I find these cut-functions more intutive, because they are in effect the “local” verson of Tellegen’s theorem.
Gerard
Both links to the papers by Jan C. Willems did not work for me (” http://homes.esat.kuleuven.be/~jwillems/Articles/JournalArticles/2007.1.pdf” and ” http://homes.esat.kuleuven.be/~jwillems/Articles/JournalArticles/2007.2.pdf”), but that seems to be a problem of the host server, not of the URL.
John wrote about Sullivan’s seminar:
None of the usual routine where everyone starts eyeing the clock impatiently as the allotted hour nears its end.
Sounds fascinating! I know of a seminar where the professor used to sleep right through all talks, would wake up in the end and - in order to prove that he paid attention - would always ask the same question: “And is your theory gauge invariant?”
Worked pretty well until once a talk was about “theories without gauge invariance”.
Tim wrote:
Both links to the papers by Jan C. Willems did not work for me (“http://homes.esat.kuleuven.be/~jwillems/Articles/JournalArticles/2007.1.pdf and “http://homes.esat.kuleuven.be/~jwillems/Articles/JournalArticles/2007.2.pdf”), but that seems to be a problem of the host server, not of the URL.
Both those links work for me now. If you’re stuck somehow, email me and I’ll mail those articles to you. They’re really cool, and I need to balance my karma.
I know of a seminar where the professor used to sleep right through all talks, would wake up in the end and - in order to prove that he paid attention - would always ask the same question: “And is your theory gauge invariant?”
Have you seen those lists of questions that are supposed to work at the end of any math talk? I can’t find them online now, but I’ve seen them posted on math professors’ doors.
Like: “Didn’t Gauss prove a special case of this result?”
Or if you want to seem more intimidating: “Didn’t Gauss prove a special case of this result in 1842?”
Or if you want to check if someone is a bullshitter: “Didn’t Gauss prove a special case of this result in 1856?”
Can anyone find those lists online?
A friend of mine who works in quantum computing once told me that he attended a talk where the speaker said, “If [a well-known difficult problem] could be solved with nineteenth-century techniques, Gauss would have solved it. Gauss is nineteenth-century complete.”
Hi John,
Do you understand Willems’s longer paper (the one in IEEE Control Systems Magazine)?
Not being an engineer and having forgotten a lot of physics, I find it hard to understand where he is coming from and what he is after.
For example, it seems strange to me to look only at curves in a configuration space (this is what I think Willems calls “behavior”) and not a flow in the phase space.
And I could only begin to guess why Willems doesn’t like the port-Hamiltonian approach.
I’d seen Richard Feynman fall asleep (or seem to) in a lecture by a visiting Physicist. At the applause, he awakens and asks a question that stuns the speaker. Such as: “That + between the first two terms back in the equation on vorticity, shouldn’t it be a minus”? Because he has always noticed something that everybody else missed.
My friend Prof. Dottie Jessup once drove Eleanor Roosevelt between two locations in Manhattan, along with another passenger (I think my mother). As they arrived, Dottie said what an honor it was for her to have assisted Mrs. Roosevelt, but what a pity it was that she’d fallen asleep and missed some interesting conversation. Eleanor Roosevelt admitted to having been asleep, but proceeded to summarize the highlights of the entire conversation.
My great-uncle, a famous portrait photographer (clients included Einstein, Ramanujan, Tagore) took a photograph of FDR that President Roosevelt particularly liked (it was before he became President). Funny story, but I seem to be on a tangent. The point is, some of us have different sleep/consciousness interfaces than others.
Descending to the mundane, way down near the end I was jarred back to reality by this:
This may sound scary, but it’s not. When we perform this process, we’re just letting ourselves take formal linear combinations of vertices, and formal linear combinations of vertices.
I would like to say I wrote that just to check if you were still awake — but alas, it was just a typo. The second appearance of “vertices” should have been “edges”.
I’ll fix it!
I think Tellegen’s theorem says that every 1-port is either giving or taking a flow of energy from the system, and the total is zero.
For instance:
-----------------
| + |
--- /
------- \
--- \
------- /
| - |
-----------------
On the left is a battery, on the right, a resistor. Whatever way you orient their arrows (the arrows are equivalent to whether you measure with red-probe-here-black-there or vice-versa), the current through the battery flows against the voltage across the battery, uphill, but the current through the resistor flows with the voltage, downhill. The battery supplies power and the resistor dissipates it. That’s probably clear.
But in answer to your question, “After all, if you have a circuit built from resistors, why should it conserve energy? Didn’t I say resistors were dissipative?” Because in a circuit built only from resistors, the voltages and currents at every port will be zero. I suppose the “obviousness” of that follows from Tellegen’s theorem with just resistors plugged into it: it tells you the situation where they both dissipate energy according to P=V2R and conserve energy!
So I guess energy enters and exits through the ports, and you can watch that happen by looking at p’q’ at a port, which can be positive or negative.
(By the way, p’q’ in your post comes out with “smart” quotes around the q, a little puzzling at first.)
Thanks for the comments! I wish I could draw p’s and q’s with dots over them in HTML. Does anyone know how? Starting in “week301” I’ll switch to a system that’s better for math symbols.
I think that in my mind, the ‘nonobviousness’ of Tellegen’s theorem arises when I — perhaps subconsciously — imagine current flowing around a loop of almost perfectly conductive wire.
If the wire were perfectly conductive, the current would keep flowing around forever once you start it up — right? But suppose the wire has a tiny bit of resistance. Then it will slowly dissipate energy — right?
So then I ask myself: how is this compatible with Tellegen’s theorem, which says the power dissipation in a closed circuit is zero?
I think maybe I understand this by now. But I think it’s better if I ask everyone reading this: what do you think about this puzzle?
If you type ͘ before a letter, it will render with a dot above it:
͘p ͘q
If you can read the rest of the math on this blog, you should be able to see those.
And for those whose eyes are not so young, avoidance of the overdot is devoutly to be wished, cf. also hardcopy publishers with weak dots.
Mike, that doesn’t really work for me (on this aged version of Firefox). The dot appears to the northwest of the letter that it’s meant to be above. If you drew a vertical line downwards from the dot, it would just miss the leftmost extreme of the letter.
That’s just so you know. Unfortunately (or fortunately if you’re Jim) I haven’t got a better suggestion.
If your trying to add a UNICODE COMBINING-DOT-ABOVE it should follow not lead. That looks like you added the dots to the preceding spaces not the letters.
Hmm, you’re right! And the combining dot I used is a two-character one. The proper thig to use seems to be q̇ (q̇), but I just get a q and a box. Seems that even with modern browsers unicode support is flaky.
It looks like it’s not a browser problem, but rather a problem with this site. I’ve verified that q̇ renders q-dot correctly in my browser when I put it on my own website. So John: use ̇ after the letter to get a dot above it in HTML.
(By the way—you might want to move this whole sub-thread over to TeXnical issues…)
aged version of Firefox
Yeah, it’s only the very most recent browsers that properly support unicode. You old browser is probably rendering them as two separate symbols. There’s precomposed p-with-dot-above (ṗ), but no q-with-dot-above, because there are no languages that use it. By the way, what do you see when I type \dot{\text{q}} ()?
What prevents you from upgrading your browser?
OK, now using a different computer with a more up-to-date version of Firefox (3.0.18). Your original p-dot and q-dot still render incorrectly, in the same way as I described. The q-dot in your message “Hmm, you’re right!”, the precomposed p-dot in your last message, and also the q-dot in your last message, are all fine. (The q of the q-dot comes out in a serif font, whereas everything else is sans.) Will try it on the old version when I get home.
As to why I haven’t got a newer version of Firefox, it’s a slightly involved and not very interesting story, which could be summarized as “too lazy”.
That’s because I was wrong! I can’t figure out why it would look even remotely correct on my browser, but there it is.
Ah, sorry, I misunderstood.
You’re right: we should move the conversation to TeXnical issues. Thanks for suggesting it.
Thanks for the suggestion, Mike! I’d been looking for something like that. The dots look pretty nice — they’re in the right place, just a bit small. Unfortunately they may cause trouble for people with aged versions of Firefox, or aged eyes. So I’ll have to think about it a bit…
(I don’t know why anyone would voluntarily stick with an aged version of Firefox — at least for me, it’s quite painless to update, and it really does get better when I update it. I wish eyes were so easy.)
So is everyone stumped by my puzzle?
I don’t know why anyone would voluntarily stick with an aged version of Firefox
My Firefox at work is the version our sys admin installs and supports. It gets upgraded when the operating system gets upgraded…I suppose there are others in the n-Cafe audience whose choice of browser is not entirely voluntary.
So is everyone stumped by my puzzle?
To be clear, does the puzzle concern a current flowing round a simple loop of wire? So to avoid your proviso “as long as the current isn’t changing too rapidly with time”, resistance will have to be extremely low. For a superconducting circuit there’s no power loss, so the question is what happens if there’s very low resistance? How low would that have to be to allow the current to flow for an appreciable time?
[John Baez: Comments aren’t working for me now.
Yes, my puzzle concerns a current flowing round a simple loop of wire. It’s easy to get the resistance of a loop of wire to be very low. In the post where I announced the puzzle, I linked to a website where you can buy a kit that’ll let you make a superconducting loop where the half-life of the current is over 1000 years.
So, assume the resistance is as low as you want….]
No. I can’t see it. Anyone else see what’s going on?
[John Baez: Perhaps just as a warmup we can write down a differential equation that seems to describe the current as a function of time, assuming a loop of wire with a small resistance. It’s not the answer to the puzzle, but I think it leads us deeper into the puzzle.]
You need a small self inductance (L) in the loop. Then the time constant will be L/R. Tellegen’s theorem continues to work: The dissipation in the resistor is equal to the rate of decrease of magnetic energy in the inductance.
Gerard
[John Baez: That sounds like it’s on the right track, but I’m puzzled.
So everyone else can follow along: I asked David to provide the differential equation describing the flow of current through a loop of wire with a tiny bit of resistance. If you look at the website for that kit I mentioned, you see the current decreases exponentially. This suggests an equation like
dI/dt = - kI
where I is the current as a function of time and k is a constant. But this equation is not the textbook equation for an RLC circuit with L = C = 0 (no inductance, no capacitance, just resistance). I wrote down the textbook equation in week288 and you’ll see that we also need a nonzero inductance. Then the RLC circuit is mathematically identical to the problem of a moving mass feeling friction proportional to its velocity. The resistance is the friction; the inductance is the mass. In other words: without the inductance, the equation for an RLC circuit does not give the current any ‘inertia’ — any ‘tendency to keep flowing’ when there’s no applied voltage.
So, one question is whether the equation for an RLC circuit is just wrong in this regime, or whether the tendency for current to keep flowing in a superconductor justly deserves to be called ‘inductance’.
But another question is: how does this square with Tellegen’s theorem, which seems to say there’s no power dissipation for a closed circuit. That was the original question.]
One thing that is perhaps a bit confusing is that the dV· I in Tellegen’s theorem isn’t really always dissipation. Specifically if you take the instantaneous dV · I for an inductor or capacitor that is losing energy, you get a negative number, equal to minus the rate of energy loss in the inductor/capacitor.
So in a resistor/inductor loop, the negative term for the inductor compensates for the positive term for the resistor.
I think for the superconducting case, the value of L is not important, as long as it is finite, so that (R/L) is zero.
Gerard wrote:
I think for the superconducting case, the value of is not important, as long as it is finite, so that is zero.
For an actual superconducting loop of wire, is small but nonzero, as I explained here. There is a slow exponential decay of the current. I pointed out a kit you can buy, where the half-life of the current is over 1000 years. But there’s always a little resistance, so the current eventually goes away.
By the way: I hope you know that you haven’t yet answered my puzzle about Tellegen’s theorem! You’ve helped a lot, but…
Here’s the puzzle. Take a loop of wire that’s almost but not quite a perfect conductor. As you say, we can think of this as a loop with a resistance and an inductance , where is small but nonzero.
Now, start some current flowing around the loop. Let time pass. Energy dissipates as time passes… it goes into heat. But Tellegen’s theorem says the total energy loss of the circuit is zero! As you put it: “So in a resistor/inductor loop, the negative term for the inductor compensates for the positive term for the resistor.”
That’s a paradox!
Or is it? Probably not: I’ve heard that just one paradox would be enough to instantly snuff out our universe. And ours still seems to be going strong.
I’m sorta depressed at how few people are taking a crack at this one…
Okay, I’ll give it a try: I guess Tellegen’s theorem, when applied to a dissipative system, is only applicable if the reservoirs are inlcuded in the description of the system. So, in the case of the lonley wire, in order to apply Tellegen’s theorem, we would have to include the dissipative process. The system looses free energy and produces entropy, so Tellegen’s theorem would read
dG/dt + T dS/dt = 0
(meaning the loss of free energy, first summand, is balanced by the production of entropy, second summand).
John wrote:
I’ve heard that just one paradox would be enough to instantly snuff out our universe. And ours still seems to be going strong.
I just can’t resist nitpicking, but isn’t a paradox a statement that only appears to be a contradiction? In order to dissolve our universe you would have to force God to contradict herself like in the movie dogma.
Addendum:
John wrote:
So then I ask myself: how is this compatible with Tellegen’s theorem, which says the power dissipation in a closed circuit is zero?
My attempt at an answer says that this claim is either wrong, namely if “closed circuit” = “the closed wire alone”, then Tellegen’s theorem is not applicable, instead of saying that the dissipation is zero. Or, if “closed circuit” = “wire + heat reservoir”, the Tellegen’s theorem is of the form stated in my previous comment and there is no contradiction (well, the statement “there is no dissipation”, if understood in the usual sense, would still be wrong).
Tellegen’s theorem works irrespective of any heat baths. Just add the dV*I for all vertices, and you will find it is zero. So it is applicable to “the closed wire alone”.
The thing is, sum (dV*I), which equals zero, is not the power loss out of the circuit. Only the edges which contain resistors contribute to that. But you always need something else than just resistors to get a circuit to run.
Gerard
I’m glad you’re zooming in on my puzzle, Gerard!
By the way, This Week’s Finds I’ve been writing for what you call , and I’ll take the liberty of translating your comment into my notation.
You wrote:
Tellegen’s theorem works irrespective of any heat baths. Just add the for all vertices, and you will find it is zero. So it is applicable to “the closed wire alone”.
Right. Let me make this painfully explicit so we can see how utterly trivial it is.
As we’ve seen, we can model “the closed wire alone” as a loop with a resistor and a conductor on it. (If we leave those out, we get a perfectly conducting loop of wire and my puzzle evaporates.)
So, draw a loop with two vertices and two edges — one edge with the resistor on it, one with the inductor on it. Orient the edges so they go around clockwise. If we assume Kirchhoff’s current law both edges have the same current flowing through it. If we assume Kirchoff’s voltage law one edge has a voltage across it, while the other has a voltage across it.
So, if we sum over the two edges, we get
Voilà! Tellegen’s theorem is true in this case! Nothing could be more ridiculously easy.
And yet, if we see what this circuit actually does, we see it loses energy: the current decays away exponentially as energy goes into heating the resistor.
The thing is, , which equals zero, is not the power loss out of the circuit.
Ah, now you’re talking!
Only the edges which contain resistors contribute to that.
Okay… so it sounds like you’re saying the real formula for the power loss of a circuit is the sum of over edges that contain resistors. Right?
Here’s another question: what is the physical meaning of Tellegen’s theorem, if any? If it’s not saying the total power lost by a closed circuit is zero, what is it saying? It’s saying something equals zero… but what’s the meaning of this ‘something’?
Everyone else is welcome to join in and play this game, by the way!
I’ll hazard a new guess that the energy lost through resistors is equal to the net work done by all other (linear, to stay close to Tellegen’s hypotheses) circuit elements. That is, capacitors and inductors can store energy, and wires can move energy between capacitors through inductors, etc.; and the net loss of energy from these stores is the phenomenon we call resistance, essentially.
In fact, we knew that already, I think? The lowest-order correction I can see here is that except at zero current and voltage everywhere, in a circuit with inductances and capacitors, the current is changing – hence also the induced magnetic field is changing, so that it radiates electromagnetic energy, too, and not just heat from the resistors.
Tim writes:
My attempt at an answer says that this claim is either wrong, namely if “closed circuit” = “the closed wire alone”, then Tellegen’s theorem is not applicable…
No, I think Tellegen’s theorem is applicable: it applies whenever we have a graph with edges labelled by voltages and currents that obey Kirchhoff’s current law and Kirchhoff’s voltage law. (Kirchoff’s current law: sum of currents flowing into any vertex is zero. Kirchoff’s voltage law: sum of voltages around any loop is zero.)
For details in this case, try this.
Or, if “closed circuit” = “wire + heat reservoir”, the Tellegen’s theorem is of the form stated in my previous comment and there is no contradiction (well, the statement “there is no dissipation”, if understood in the usual sense, would still be wrong).
There may be a way to apply Tellegen’s theorem to a kind of generalized ‘circuit’ that includes the heat reservoir as well as the wire. And then perhaps Tellegen’s theorem becomes conservation of energy. That’s a very interesting idea. But right now I’m in the mood to track down the meaning of Tellegen’s theorem as applied to just the loop of wire alone.
Why? Mainly because this illustrates the version of Tellegen’s theorem that electrical engineers actually use. The closed loop of write is sort of a trivial example of an electrical circuit, but for that reason it may help clarify what Tellegen’s theorem actually means.
Tellegen’s theorem for resistors: Thanks to Gerard and John for the answers, I think I get now why I was wrong; I mean the statement “Tellegen’s theorem is not applicable to the closed wire alone”: I tried to formulate a version where the heat reservoir is a vertex of the graph representing the system and the dissipative process flows along the edge connecting it with the part representing the wire.
The problem is that I was thinking of general graphs where vertices may represent whole subsystems, in the sense of the “zooming” of Willems we would have multiple levels of abstraction, one graph representing the system on each level, and therefore vertices and edges of different semantics on each level.
Why the silence: Since I’m participating I won’t be able to resolve the mystery of silence, but I noted that you wrote “this stuff is incredibly important” - why? Is there a tagline like “This lecture is about the Dirac equation. It is the equation for electrons and positrons and therefore describes half of the matter of the universe” - that’s my favorite intro to a QFT lecture.
physical meaning of Tellegen’s theorem:
John wrote:
…it applies whenever we have a graph with edges labelled by voltages and currents that obey Kirchhoff’s current law and Kirchhoff’s voltage law.
Kirchoff’s circuit laws are a consequence of conservation laws (energy and charge), which makes me doubt that Tellegen’s theorem - understood as you describe it - contains more physics than these. Is there a hint why this may be so nevertheless?
P.S.: John wrote:
As we’ve seen, we can model “the closed wire alone” as a loop with a resistor and a conductor on it.
The “conductor” is a typo, you mean “inductor” :-)
Tim wrote:
Tellegen’s theorem for resistors: Thanks to Gerard and John for the answers, I think I get now why I was wrong; I mean the statement “Tellegen’s theorem is not applicable to the closed wire alone”: I tried to formulate a version where the heat reservoir is a vertex of the graph representing the system and the dissipative process flows along the edge connecting it with the part representing the wire.
Right — that’s a clever and possibly useful idea, but apparently not necessary to resolve the ‘paradox’ I was trying to torture us with.
The problem is that I was thinking of general graphs where vertices may represent whole subsystems, in the sense of the “zooming” of Willems we would have multiple levels of abstraction, one graph representing the system on each level, and therefore vertices and edges of different semantics on each level.
Bond graph people use graphs where different edges represent effort-flow pairs of different types: electrical, mechanical, thermal, and so on. Each ‘type’ is an object in a symmetric monoidal category — just like each ‘type of particle’ labelling an edge in a Feynman diagram, or each ‘data type’ in functional programming… or each ‘type’ in type theory.
As you may know, I love this collection of analogies. So, I like your idea of taking an electrical circuit and thinking of it as part of a larger electro-thermal ‘circuit’ where resistors turn energy from one type into another. It would be worth trying to develop it and make it precise.
Why the silence: Since I’m participating I won’t be able to resolve the mystery of silence, but I noted that you wrote “this stuff is incredibly important” - why? Is there a tagline like “This lecture is about the Dirac equation. It is the equation for electrons and positrons and therefore describes half of the matter of the universe” - that’s my favorite intro to a QFT lecture.
Well, when I wrote “this stuff”, I was referring to the idea that entropy production is minimized by some class of open systems that are not in equilibrium, but are in ‘steady state’, with power flowing through them.
For example: sunlight falling on the ground which re-radiates it into the infrared. Or: electrical current flowing through a network of resistors, which produce heat. Or: a pot of water on a stove with burner set very, very low.
These situations are incredibly common and important in everyday life, and they deserve to be studied with all the tools that modern mathematical physics possesses. So it’s a bit of a scandal if there’s something called ‘Prigogine’s theorem’ that gives conditions for when these situations occur, which is sort of a theorem, but hasn’t yet been turned into an actual theorem of the sort a mathematician can understand.
Quite possibly it has, and we just haven’t found the right references so far. The references we’ve found so far show a result that’s on the road to mathematization, but hasn’t quite made it there yet.
The paper Desoer and Oster is intriguing because it suggests that there’s a relation between Prigogine’s theorem and chain complexes. I’ve tried to push this one step further. But there’s a lot more to be done.
John wrote:
So it’s a bit of a scandal if there’s something called ‘Prigogine’s theorem’ that gives conditions for when these situations occur, which is sort of a theorem, but hasn’t yet been turned into an actual theorem of the sort a mathematician can understand. Quite possibly it has, and we just haven’t found the right references so far.
Maybe, but if it has then it’s hard to find, at least if one employs my search strategy (looking at books about non-equilibrium thermodynamics and diverse synonyms, as well as googling for “irreversible linear processes” etc).
I stubled upon an interesting paper, however, that claims to prove Prigogine’s theorem via a more general variational principle called Ziegler’s principle. This is a formulation of the maximum entropy production principle (MEPP), valid in nonlinear regimes (Prigogine’s theorem isn’t, as we already know, apparently Prigogine himself constructed nonlinear examples that violate his theorem).
BTW (completly off topic, concering career changes): In a different context I stumbled upon this remark of Paul Halmos in his book “I want to be a Mathematician” (the paragraph has the title “The beginning of Hilbert space”):
…to stay young, you have to change fields every five years…it works. A creative thinker is alive only so long as he grows; you have to keep learning new things to understand the old. You don’t really have to change fields - but you must stoke the furnace, branch out, make a strenuous effort to keep from being locked in.
There are some more papers making a similar claim (Prigogine’s theorem is a consequence of a maximum entropy production principle), here is one:
which has a follow up here:
Tim wrote:
I stubled upon an interesting paper, however, that claims to prove Prigogine’s theorem via a more general variational principle called Ziegler’s principle. This is a formulation of the maximum entropy production principle (MEPP), valid in nonlinear regimes…
I’ll have to look at that. I hope you realize how odd it sounds to derive Prigogine’s principle of minimum entropy production from a principle of maximum entropy production!
It’s a measure of my ignorance — or perhaps the confusion of the whole subject of nonequilibrium thermodynamics — that I’ve seen references to principles of minimum entropy production and also maximum entropy production, without ever seeing anyone discuss the question “Is only one of these true, or are both true — but under different conditions?”
I know for sure that electrical circuits made of linear resistors obey the principle of minimum entropy production… and therefore, a whole range of analogous systems do the same.
I’ve never yet seen an example of a system that maximizes entropy production.
Halmos wrote:
…to stay young, you have to change fields every five years…it works. A creative thinker is alive only so long as he grows; you have to keep learning new things to understand the old. You don’t really have to change fields - but you must stoke the furnace, branch out, make a strenuous effort to keep from being locked in.
I think something like this is true. In fact I’ve seen a study of academics that claimed to show that the well-known pattern of diminished creativity with increasing age is an illusion. It said that what matters is not age so much as how long you have worked in the same field. They said that whenever anyone starts working in a new field, their production of good new ideas quickly climbs and then slowly decreases. Their evidence came from people who switched careers in mid-life.
I can’t find this study now, so this is a vague description. But it seems plausible.
I think that when you start work on a new subject you have not yet adapted yourself to all the ‘conventional wisdom’ in the subject. So, you have a bunch of radical ideas that go against the conventional wisdom. Most are wrong but some are right. Later, you get more and more used to the conventional wisdom — perhaps the new conventional wisdom which your work helped define! So, your contributions become less creative.
I can see this happening to me in -category theory. The biggest, most radical ideas came right near the start. Ever since then my creativity has been going down, while my technical expertise has been rising. If I let this continue in its natural way, I might eventually become an esteemed old expert in higher category theory. I wouldn’t have many big new ideas anymore — but I’d be well equipped to learn the work of younger, more creative scholars, and perfectly suited to explain it, perhaps in a nicely written series of textbooks.
That wouldn’t be bad. But I think it’ll be more interesting to try something else.
John wrote:
I hope you realize how odd it sounds to derive Prigogine’s principle of minimum entropy production from a principle of maximum entropy production!
Yes, I do, as did Martyusheva and Seleznev when they wrote their paper, here is an excerpt:
1.2.6. The relation of Ziegler’s maximum entropy production principle and Prigogine’s minimum entropy production principle
If one casts a glance at the heading, he may think that the two principles are absolutely contradictory. This is not the case. It follows from the above discussion that both linear and nonlinear thermodynamics can be constructed deductively using Ziegler’s principle. This principle yields, as a particular case (Section 1.2.3), Onsager’s variational principle, which holds only for linear nonequilibrium thermodynamics. Prigogine’s minimum entropy production principle (see Section 1.1) follows already from Onsager–Gyarmati’s principle as a particular statement, which is valid for stationary processes in the presence of free forces. Thus, applicability of Prigogine’s principle is much narrower than applicability of Ziegler’s principle.
John wrote:
It’s a measure of my ignorance — or perhaps the confusion of the whole subject of nonequilibrium thermodynamics — that I’ve seen references to principles of minimum entropy production and also maximum entropy production, without ever seeing anyone discuss the question “Is only one of these true, or are both true — but under different conditions?”
Sigh. I guess the papers I mentioned are not the final account of the story, I also read papers claiming that Ziegler’s principle is applicable to the linear regime only (the one by Bruers states that, I think), that both principles are wrong (Zeigler’s and Prigogine’s), etc.
John wrote:
I’d be well equipped to learn the work of younger, more creative scholars, and perfectly suited to explain it, perhaps in a nicely written series of textbooks. That wouldn’t be bad. But I think it’ll be more interesting to try something else.
Does that imply that the textbook on higher category theory will not be completed? Doh!
John wrote
I think that when you start work on a new subject you have not yet adapted yourself to all the ‘conventional wisdom’ in the subject. So, you have a bunch of radical ideas that go against the conventional wisdom. Most are wrong but some are right. Later, you get more and more used to the conventional wisdom — perhaps the new conventional wisdom which your work helped define! So, your contributions become less creative.
I think that, in addition to a “raw” creativity effect, there’s also the fact that if you haven’t been working in the new field until you switch into it, by definition you’ve been working on some other topics with a different “basic worldview” which gives you different “raw materials” for “building” your ideas to others. I’m sure that some of your most “powerful” ideas will come from being a mathematical physicist transported into an area where those viewpoints aren’t common currency.
It’s good to see we’re not getting too far away from earlier Café interests. Back here, Jayne’s maximum caliber principle cropped up, allowing for a variational treatment of irreversible processes. It would be great if what you have been speaking about in this thread is an aspect of matrix mechanics.
The caliber of a space-time process thus appears as the fundamental quantity that “presides over” the theory of irreversible processes in much the same way that the Lagrangian presides over mechanics. That is, in ordinary mechanics we learn first that a variational principle (minimum potential energy) determines the conditions of stable equilibrium; then we learn how to generalize this to the Lagrangian, whose variational properties generate the equations of motion. In close analogy, Gibbs showed that a variational principle (maximum entropy) determines the states of stable thermal equilibrium; now we have learned how to generalize this to the caliber, whose variational properties generate the “equations of motion” of irreversible processes. (Jaynes, Macroscopic Prediction)
John wrote:
I think that when you start work on a new subject you have not yet adapted yourself to all the ‘conventional wisdom’ in the subject. So, you have a bunch of radical ideas that go against the conventional wisdom.
And the latter may sometimes be wrong! I have a biologist friend who has examples of what was at one time the perceived conventional wisdom so strongly ‘believed’ by the community that it required a paradigm shift even to admit the ‘possibility’ of an alternate interpretation of the known facts.
John Baez wrote:
It’s a measure of my ignorance — or perhaps the confusion of the whole subject of nonequilibrium thermodynamics — that I’ve seen references to principles of minimum entropy production and also maximum entropy production, without ever seeing anyone discuss the question “Is only one of these true, or are both true — but under different conditions?”
I tried to figure this out. I will use the principle of “minimum” dissipation here, instead of entropy production, but the idea is the same. A first clue: Remember we figured out that the dissipation in the resistors is minus the ∑i(Vi-Vj)⋅Iij of the energy storing components (inductors, capacitors)? Well, if the first is minimal, then the second must be maximal. Maybe it is more correct to say “extremal dissipation”.
First, note that the extremum (i.e. either minimum or maximum, the derivative with respect to a variation being zero) only applies within constraints. For example, if you are allowed to change an individual current, then you can easily see that the dissipation is not in an extremum: The power is proportional to I, so there is no extremum. However,you can recover the circuit equations from the power, expressed as ∑ij(Vi-Vj)2/Rij, by demanding that the derivatives with respect to Vi are all zero. So the extremum is with respect to voltage variations, keeping Ohm’s law exact, and allowing Kirchhoff’s current law to be infinitesimally violated.
Now let’s see if we have a maximum or a minimum. Suppose we are at a vertex with voltage Vi. We wobble it slightly to Vi + δV.
Old dissipation around that Vi:
∑j(Vi-Vj)2/Rij
New dissipation around that Vi:
∑j(Vi + δV-Vj)2/Rij
Difference:
(δV)2 ∑j 1/Rij + δVj(Vi-Vj)/Rij
The first order term in δV is zero, due to Kirchhoff’s current law, so:
δP = (δV)2 ∑j 1/Rij (eq 1)
So now we can figure out if we have a maximum or minimum. The last equaiotn shows that we have an extremum: There is no first order variation in the power (P) due to (δV).
We can also see that we are in a minimum *if* ∑j 1/Rij is positive. This will be the case if we are somewhere in a resistor network. But what about inductors and capacitors?
Electrical engineers like to use complex impedances (Z) for the inductor Z=jωL and capacitor Z=1/(jωC). I remember learning this, this was when I first started liking complex numbers: You can continue to use circuit analyses, but now it works seamlessly for time-dependent components.
So according to eq 1, if we use complex impedances, we get that the extremum is neither minimum or maximum, but a complex number.
However electrical engineers are interested in signals for exp(-iωt), this is why the impedances have jω in them. In our case however, it is more appropriate to look at signals that are like exp(-t/τ). We are not looking at oscillations, but (thermal) systems that decay exponentially with time. In that case, the impedances are:
Inductor: Z = -L/τ
Capacitor: Z = -τ/C
So at last, we can see that for energy storing components, in a thermal setting, the dissipation is in a *maximum* with respect to δV. If you are in a vertex with resistors, then you are in a *minimum* with respect to δV.
For practical purposes, you don’t usually care, because you use only the extremum condition, to recover the equations from the mimimum principle.
As for entropy production, this is analogous: It can be either maximal or minimal, depending on the type of vertex. If you look at the heat baths, it is maximal. If you look at the conductors, it is minimal.
Also interesting is the analogy with “Least” Action. In the space time circuit, you have both negative and positive resistors, so action is extremal, but not always minimal. Perhaps interesting: According to Tellegen’s theorem, Action is not just extremal, but *equal to zero* if integrated over a closed system!
Gerard
Some corrections/ clarifications:
I wrote:
For example, if you are allowed to change an individual current, then you can easily see that the dissipation is not in an extremum: The power is proportional to I, so there is no extremum.
In that case, we would be varying I independent of V. If we couple them through Ohm’s law, the The power is proportional to I2. In the latter case, there is an minimum for I=0. But that is not the mimimum we seek: The minimum with respect to voltage variations gives the right answer. (This is something I don’t quite understand as well as I would like. I saw John writing someting about cohomology…)
Anyway, the key to the minimum/maximum issue is I think the equation for δP as a function of δVi:
δP = (δVi)2 ∑j 1/Rij
Gerard
John wrote:
I hope you realize how odd it sounds to derive Prigogine’s principle of minimum entropy production from a principle of maximum entropy production!
Tim wrote:
Yes, I do, as did Martyusheva and Seleznev when they wrote their paper; here is an excerpt:
1.2.6. The relation of Ziegler’s maximum entropy production principle and Prigogine’s minimum entropy production principle
If one casts a glance at the heading, he may think that the two principles are absolutely contradictory. This is not the case. It follows from the above discussion that both linear and nonlinear thermodynamics can be constructed deductively using Ziegler’s principle.
Oh, good! I’ll have to see how they pull this rabbit out of the hat.
Sigh. I guess the papers I mentioned are not the final account of the story; I also read papers claiming that Ziegler’s principle is applicable to the linear regime only (the one by Bruers states that, I think), that both principles are wrong (Zeigler’s and Prigogine’s), etc.
It would be very interesting if such incredibly important issues have not been settled! It could make a great area for research!
But it’s hard for me to tell if this is true. For every well-understood question in physics one can find papers arguing that the consensus view is wrong. So often one needs to study a subject for a while, even get to know the experts, to see what counts as ‘well understood’, ‘an open question’, or ‘a hopelessly difficult question’.
I do want to understand nonequilibrium thermodynamics and these minimum and maximum principles, so I’ll keep chewing away at them, and keep reporting back in This Week’s Finds.
By the way: surely it would be misleading to say that Prigogine’s principle of minimum entropy production is merely ‘wrong’. It’s true under certain conditions, and it’s our job — if nobody else has done it yet — to say exactly what these are.
Anyway, I’ll read the paper by Martyusheva and Seleznev and see what they say.
John wrote:
I’d be well equipped to learn the work of younger, more creative scholars, and perfectly suited to explain it, perhaps in a nicely written series of textbooks. That wouldn’t be bad. But I think it’ll be more interesting to try something else.
Tim wrote:
Does that imply that the textbook on higher category theory will not be completed?
It was going to be a series of textbooks… an intimidatingly large task. I may still write some of these books. But to some extent I’ve discharged my obligation by writing those Lectures on cohomology and n-categories along with the Rosetta, Prehistory and Invitation papers. And I decided I’ll be happier thinking of these textbooks as projects I might do rather than projects I must do. If I get really involved with combating global warming or the mass extinction event, it may seem silly to spend time teaching people -categories. Or, it may seem like an enjoyable hobby — and a good way to keep up my math skills! I can’t tell yet. So, I feel better leaving the future open-ended.
Just a short explanation why maximum and minimun entropy production are not contradictory, for those who don’t have the time to read the papers:
Bake a cake and put it - while still hot - on a table in your garden in the sun, this is a system that is neither in equilibrium nor in a steady state.
The cake will dissipate the heat, the (or rather several of the proposed) principle(s) of maximum entropy production says that it will do it in such a way that the maximum amount of entropy is created in every instant, as long as it fits the constraints.
Finally it will reach a steady state where the heat it dissipates matches the energy it absorbs from the sun, and this is the only influence that keeps its temperature above that of it’s surroundings.
In the steady state, all heat that the cake can dissipate - in addition to the energy turned in to heat that it gets from the sun - has been dissipated, so the steady state is the state of minimum entropy production by the cake (of all possible states, says Prigogine, but for starters one can concentrate on all states actually observed between putting the cake on the table and the cake reaching the steady state).
Thermal force = light from the sun.
Thermal flux = heat dissipated by the cake.
Constraints: energy conservation, temperature of garden air and table, being a cake etc.
John wrote:
It would be very interesting if such incredibly important issues have not been settled! It could make a great area for research!
I have no idea, I knew nothing about the whole topic before you mentioned Prigogine’s theorem, but I noted that the Wikipedia page about maximum entropy production and related topics has not reached the state of maturity that I’m already used to (for undisputed, mature technical topics).
I was startled when I encountered this in grad school (1973-1977) that the literature on nonlinear dynamics in the fluxes of metabolisms that I could find had never done a perturbation expansion in the neighborhood of steady state. So I did, and got what I thought were nice results, published in peer-reviewed venues. But there were were several levels of analysis to do. One was via convolution integrals, looking at the response of the nonlinear differential equations to a Dirac delta input. One was the old-school approach with matrix exponentials. The most compact approach was with Krohn-Rhodes decomposition of the semigroup of differential operators.
But, alas, the Math/CS folks were unclear on the distinction between “Equilibrium” and “Steady State” and the Biology folks were unfamiliar with facts such as that the convolution defines a product on the linear space of integrable functions. This product formally means that the space of integrable functions with the product given by convolution is a commutative algebra without identity (Strichartz 1994, §3.3). Other linear spaces of functions, such as the space of continuous functions of compact support, are closed under the convolution, and so also form commutative algebras. Nor were they familiar with the conventional approach to relating input and output through a Transfer Function and the use of Laplace transforms. It’s the perils of interdisciplinary work. Which is part of why I love how John Baez et al tackle this unified vision.
Minimum and maximum entropy production principles:
I should of course have started my explanation by this statement:
The maximum entropy production principles (MEPPs) consider systems away from equilibrium and steady states. The main theorems of thermodynamics say that the system will reach equilibrium if isolated, or the steady state if external “forces” are present, and stay there. The MEPP now try to predict in addition which macroscopic path the system will take: This will be the path where on each instant the amount of entropy produced by the system will be a maximum.
In this sense MEPPs are an extension of the second law of thermodynamics (the entropy will always increase).
The steady state has to be the one of all states accessible to the system where the production of entropy is at a minimum, because if it were not, it would not be stable (compare this to the definition of a stable state in mechanics).
Prigogine’s theorem says that the stable state is the state of minimum entropy production, so that it is a consequence of MEPPs as described above.
The real problems start once one tries to make all this handwaving precise, of course.
JB: I do want to understand nonequilibrium thermodynamics and these minimum and maximum principles, so I’ll keep chewing away at them, and keep reporting back in This Week’s Finds.
There has been much progress since Prigogine, but there are still many interesting open problems!
Let me again strongly recommend reading the books
Hans C. Oettinger, Beyond Equilibrium Thermodynamics, Wiley 2005. https://www.polyphys.mat.ethz.ch/research/books/hco_bet/ApplRheol_0471666580_review.pdf
A.N. Beris and B.J. Edwards, Thermodynamics of flowing systems with internal microstructure, New York 1994.
H.P. Breuer, F. Petruccione, The theory of open quantum systems, Oxford University Press 2002. http://www.lavoisier.fr/notice/fr417156.html – http://www.gbv.de/dms/goettingen/372695639.pdf
Did you already recommend these books to me? Sorry! I must be going senile.
I’ll get ahold of them. I figured there must be a lot of good work since Prigogine’s, since he won the Nobel prize for it — that’s usually enough to trigger a flood of followups. But so far most the books I’ve found are rather unsatisfying.
JB: Did you already recommend these books to me? Sorry! I must be going senile.
You even wrote somewhere that ”someone mentioned the book by Beris and Edwards”….
Maybe I recommended them not here but on s.p.r., replying to your This Week’s Find posting there when you started signalling your interest in dissipative physics a few months ago. Probably it didn’t sound enough of a recommendation. Therefore, this time, I used more explicit words and added links to reviews, hoping to better catch your attention.
JB: But so far most the books I’ve found are rather unsatisfying.
These books are not perfect, otherwise there would nothing be left to do.
But they are very interesting and contain really a lot about dissipative physics, whereas in textbooks one usually only finds the conservative case discussed. Nature is always dissipative, while it is conservative only in the idealization where one can disregard thermal effects. So the dissipative case should get much more attention than it gets.
Beris and Edwards promote the Poisson bracket view of dissipative systems arising in rheology - the flow of material with microstructure. In conservative mechanics, the Liouville equation expresses the time derivative of a density as a Poisson bracket of the density with the Hamiltonian. In the dissipative case, there are additional terms depending on a dissipative bracket (which often may be viewed as brackets of brackets - cf. the dissipative terms introduced into conservative fluids by second-order derivatives, with prototype the heat equation and Navier-Stokes).
Oettinger discusses a very general scheme which encompasses – in addition to the Beris/Edwards stuff (which it generalizes, but B/E have much more detail on individual Poisson brackets for actual applications) – lots of other interesting classical dissipative systems: from chemical reactions to Boltzmann equations to general relativity.
Supposedly, every interesting dissipative system in Nature fits into Oettinger’s generic scheme.
Breuer and Petruccione discuss the quantum version. Here the von Neumann equation expresses the time derivative of a density operator as a commutator bracket of the density with the Hamiltonian. In the dissipative case, there are additional terms of Lindblad form, which can always be written in terms of two iterated commutators. (Lindblad equations are routinely needed in quantum optics, where accounting for dissipative losses is essential for many applications.)
So the dissipative case is a very natural extension of the conservative case. In fact, as in the conservative case, the classical and the quantum version can be treated on very similar footing. This is not apparent from the three books, but a bit is outlined in the second half of Chapter 1 of my Theoretical Physics FAQ at http://www.mat.univie.ac.at/~neum/physfaq/physics-faq.html , and this is only the tip of an iceberg.
Mathematically, the theory is not yet as nicely polished as Hamiltonian (classical or quantum) mechanics is. But well, this leaves room for new research of more theoretically minded people!
David wrote:
It’s good to see we’re not getting too far away from earlier Café interests. Back here, Jayne’s maximum caliber principle cropped up, allowing for a variational treatment of irreversible processes.
Holy moly! Why didn’t you remind me of this sooner?!
Well, it’s not your fault… it’s mine for not remembering you mentioned it 3 years ago. I’ve always been in love with variational principles. But iIn the last few weeks I’ve been desperately trying to find some sort of variational principle that applies to irreversible processes. I guess I just didn’t know the right buzzwords!
Thanks! This could be great. Especially since Jaynes was no dope.
I wonder what current thinking is about the differences between Prigogine and Jaynes’s approaches. I remember a review from about the time of my PhD studies which concluded that they led to broadly the same results. Let’s see, I think it was J. P. Dougherty, Foundations of Non-Equilibrium Statistical Mechanics.
I’ve long been interested in how far one can proceed adopting the Jaynesian approach. It’s intriguing that so much can be achieved by thinking about inference under conditions of imperfect knowledge. We had a little on this in the early months of the blog, e.g. here where Caticha is quoted:
The point of view that has been prevalent among scientists is that the laws of physics mirror the laws of nature. The reflection might be imperfect, a mere approximation to the real thing, but it is a reflection nonetheless. The connection between physics and nature could, however, be less direct. The laws of physics could be mere rules for processing information about nature. If this second point of view turns out to be correct one would expect many aspects of physics to mirror the structure of theories of inference.
John Baez wrote:
But Tellegen’s theorem says the total energy loss of the circuit is zero!
Only the resistor is actually losing energy *out of* the circuit. The inductor loses energy, but it pumps it into other parts of the circuit. No energy leaves the circuit through the inductor. If you want to figure out how the power flows through the circuit, you can use the “cut functions” I described in my other post.
Circuits with resistors have a problem. If the resistors are all positive, then the only solution is zero current everywhere. If some resistors are negative, there could be other solutions if the determinant of the matrix for the voltage equations is exactly zero. This is like an eigenmode of the circuit: If there is some capacitor or inductor, then for some omega, you have non-zero solutions V_i*exp(omega*t)
Gerard
John Baez wrote:
But Tellegen’s theorem says the total energy loss of the circuit is zero!
I hope by now it’s clear that this is wrong.
I’m sorta depressed at how few people are taking a crack at this one…
Did Tim and Gerard’s answers not lift the gloom? Perhaps if you spoon feed us the first answer, the class will improve for the next question.
David wrote:
Did Tim and Gerard’s answers not lift the gloom?
Yes. And Gerard’s most recent reply makes me even happier.
It’s sort of weird that with all the super-geniuses who read this blog, only a few people were willing to take a crack at this puzzle. I can’t tell if it was too easy for most people, or too hard. Perhaps the mathematicians didn’t like how it was a bit vaguely phrased… but of course that vagueness is the key to any ‘paradox’: once the vagueness is precisely penetrated, the paradox dissolves.
But let’s march on!
Sorry I haven’t been paying attention here. I’ve spent the last week trying to understand some elementary category theory :)
Here is a possible hint (as if I knew the answer). Note that KVL and KCL are both valid even when voltages and currents are complex and then “think like an engineer”.
I’m not sure if this is particularly helpful or not (yet), but thought I would throw it out there before I hit the sack (it’s after 3:00am!). This is the approach I would take to trying to understand what is going on.
John, I never understood what the paradox was or how it got resolved, but you ask,
“…what is the physical meaning of Tellegen’s theorem, if any? If it’s not saying the total power lost by a closed circuit is zero, what is it saying? It’s saying something equals zero– but what’s the meaning of this ‘something’?”
(By the way, resistors aren’t the only kind of circuit part that can dissipate energy. Antennas and LEDs are other examples.)
What Tellegen’s theorem says to me is that the ideal wires don’t contribute, store, or take away energy. They just convey energy between the other components. (But I think I’m not getting what you mean by a physical meaning.)
I don’t think we beat the ideal-vs-real / “current in a loop of wire” thing to death either. So here I go!
For a while I wanted to say that current just can’t flow in a loop of ideal wire, that it’s topologically a point, so your question is like “How much number flows in an equal sign?” Finally I realized: the rules say the current can be anything. They also don’t specify any relation to the current an instant ago.
The instant you add resistance, though, the rules say there is no current. Not that it goes to zero, just that now we know there isn’t any. An ideal wire-resistor loop doesn’t dissipate energy, it just never had any, has nothing that can hold any.
(Undefined current is like the absolute voltage of something that has no connection at all to a reference point. They call it “floating.” In reality there’s capacitance between everything, but ideally both the voltage and current can be undefined.)
A superconducting loop in real life has current only because it’s an inductor. (Or, whatever the explanation it should formally be an inductor.) An ideal inductor-wire loop has a constant current.
A more realistic inductor-resistor loop transfers energy from somewhere represented by the inductor, to somewhere represented by the resistor. But the energy flows balance, that’s what’s “conserved,” I guess that was the resolution to the paradox.
(Real real wires are like infinite series of infinitesimal resistors and inductors, connected to the universe at every point by infinitesimal capacitors. Fluctuations in voltage and current propagate through wires across space at a finite speed, it’s weird. And I left out that space itself carries on like that. I mean, e.g., empty space has an impedance of 377 Ohms.)
John, I never understood what the paradox was or how it got resolved….
Well, as soon as you understand a paradox, it’s not a paradox anymore. But I think you actually understand it very well, since you’ve explained the answer better than anyone else!
For a while I wanted to say that current just can’t flow in a loop of ideal wire, that it’s topologically a point, …
A loop is not topologically a point.
Finally I realized: the rules say the current can be anything. They also don’t specify any relation to the current an instant ago.
Right, if by “the rules” you mean Kirchhoff’s voltage and current laws — which are the only laws needed to derive Tellegen’s theorem.
The instant you add resistance, though, the rules say there is no current. Not that it goes to zero, just that now we know there isn’t any.
Right — where now “the rules” include Ohm’s law, saying that current is proportional to voltage. Kirchhoff’s voltage law says that the voltage across a wire that goes around in a loop must be zero. So then Ohm’s law says the current is zero.
Part of the “paradox” pitted this mathematical fact against our physical intuition that current can flow around a loop of wire with a very small resistance, like a superconducting loop. The mathematical fact is true, our physical intuition is true, but they are not really in conflict, since:
A superconducting loop in real life has current only because it’s an inductor. (Or, whatever the explanation it should formally be an inductor.)
Well put! It took me a while to realize this. I would still like to understand the physical mechanism whereby a supercounducting loop becomes ‘formally’ an inductor. Why does the current keep going around? Is it mainly inductance in the usual sense, which can be thought of as conservation of energy, or is it mainly conservation of angular momentum?
There is vast and complicated but fascinating literature on Superconductivity, since Dutch physicist, Heike Kamerlingh Onnes, was credited
with discovering superconductivity in 1911, work for
which he was awarded a 1913 Nobel Prize, and which I feel answers’s John Baez’s questions. There is a great chance to publicize what is known for the Centenary, next year.
To begin with, a superconducting current in a loop does NOT last forever.
One might reasonably start a survey with Ginzburg–Landau theory, named after Vitaly Lazarevich Ginzburg and Lev Landau, a mathematical theory used to model superconductivity. This does not purport to explain the microscopic mechanisms giving rise to superconductivity. Instead, it examines the macroscopic properties of a superconductor with the aid of general thermodynamic arguments, and is phenomenological, describing some of the phenomena of superconductivity without explaining the underlying microscopic mechanism.
Most recently:
arXiv:0906.0831
Title: Defying the fine structure constant: single Cooper pair circuit free of charge offsets
Authors: Vladimir E. Manucharyan, Jens Koch, Leonid Glazman,
Michel Devoret (Yale University, Physics and Applied Physics
departments, New Haven, CT, USA)
Subjects: Mesoscale and Nanoscale Physics (cond-mat.mes-hall);
Superconductivity (cond-mat.supr-con)
The promise of single Cooper pair quantum circuits based on tunnel junctions for metrology and quantum information applications is severely limited by the influence of “offset” charges – random, slowly drifting microscopic charges inherent to many solid-state systems. A remedy is to shunt the junction with a sufficiently large
inductance. However, the small value of the fine structure constant imposes a fundamental incompatibility between shunting with a
wire-wound inductor and providing correct electromagnetic environment for single Cooper pair effects. By employing the Josephson kinetic
inductance of a series array of large capacitance tunnel junctions, we have solved this conundrum and realized a new superconducting artificial atom. Its energy spectrum manifests the anharmonicity
associated with single Cooper pair effects combined with total insensitivity to offset charges.
Also note this duality:
Apr 2, 2008
Physicists discover the ‘superinsulator’
An international team of researchers has discovered what it describes as the reverse side of a superconductor — a “superinsulator” that
indefinitely retains electrical charge.
Christoph Strunk of Regensburg University in Germany, whose team includes Valerii Vinokur of Argonne National Laboratory in the US and
other colleagues from Germany, the US and Belgium, found the state in thin films of titanium nitride cooled towards absolute zero in a magnetic field. Although the material is usually a superconductor, in which electrical current can propagate without resistance, the team have found that in these conditions the material’s resistance rises to
infinity (Nature 452 613).
“In the 1990s it became apparent in a number of measurements that a quantum phase transition — that is, a transition between two ordered states at zero Kelvin — is a great place to look for new kinds of
ordered states,” says Stephen Julian, a low-temperature physicist at the University of Toronto, Canada. “This [research] seems to be quite
an unexpected and beautiful example of this: a superinsulator on the boundary between the ordinary insulator and the superconducting ground
state.”
Superconducting ‘puddles’
In a superconductor, the lack of resistance arises because electrons bind together into pairs called Cooper pairs. These pairs act collectively, moving as single quantum entity. When a superconducting
material is flattened into a granular film, however, the entity becomes partitioned. Strong disorder forces the Cooper pairs into isolated “puddles” separated by insulating regions known as Josephson junctions, and individual Cooper pairs can only pass between puddles by quantum tunnelling.
Physicists have previously found that, very near to absolute zero, the insulating regions can become clogged with charge, blocking the flow of current. But Strunk, Vinokur and colleagues have found that, given a magnetic field of 0.9 T, their films of titanium nitride persist with this zero-conduction state as warm as 70 mK.
To explain this superinsulation, in which current is blocked even at finite temperature, the team has suggested the roles of charge and magnetic flux become mirrored. In the superconducting phase, a
magnetic field penetrates the material in quanta called vortices, which rotate in alternate directions. The Cooper pairs are free to
circulate the vortices by tunnelling between puddles.
But in the superinsulating phase, the roles of charge and vortices are swapped. Vortices circulate bound pairs of opposite charge, which prevents a current from flowing. “A superinsulator cannot appear at all without the existence of superconductivity in the same film,”
explains Vinokour. “That is why we refer to the superinsulator as the reverse side of superconductivity.”
Alain Bossavit was unable to comment on the -Café, so he emailed Robert Kotiuga who emailed me. Alain wrote:
I’d wish to point out that this Prigogine’s “theorem of minimum entropy production” is not as general as one might believe, or wish. Its validity is severely restricted. See the comment on
I. Danielewicz-Ferchmin, A.R. Ferchmin: “A check of Prigogine’s theorem of minimum entropy production in a rod in a non-equilibrium stationary state”, Am. J. Phys., 68, 10 (2000), pp. 962-5
by
P. Palffy-Muhoray, Am. J. Phys., 69, 7 (2001), pp. 825-6
where P.-M. shows that the “theorem” does not hold: “Stationary states can be shown to correspond to minimum entropy production only when the Onsager coefficients are constant.” He was seconded by
W.G. Hoover, Am. J. Phys., 70, 4 (2002), pp. 452-4.
I find Alain Bossavit’s remarks very tantalizing, because I have not yet found mathematically precise statement and proof of ‘Prigogine’s theorem’.
I also don’t understand the relation between the ‘Prigogine’s theorem’ mentioned here:
and the theorem I often hear about (but have never seen precisely stated or proved), which says something like ‘entropy production is minimal in a stationary state’.
Does anyone know a precise statement and proof of Prigogine’s theorem???
John wrote:
Does anyone know a precise statement and proof of Prigogine’s theorem???
Did you have a look at his book Modern Thermodynamics: From Heat Engines to Dissipative Structures (amazon) ?
Here chapter 17.2 is about the “Theorem of Minimum Entropy Production”.
But I don’t think that there is a theorem in the sense of mathematics or physics, it is more a guiding principle (that can be illustrated by concrete examples), and that would be (quoting from the book that quotes from Prigogine’s original papers):
“In the linear regime, the total entropy production in a system subject to flow of energy and matter, the production of entropy reaches a minimum value at the nonequilibrium stationary state.”
This chapter explains this principle with 5 concrete systems (chemical reactions, thermal conduction and electrical circuits). Should fit snugly with the recent editions of This Week’s Finds :-)
In modern terminology, life is a dissipative system. A dissipative system is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. The term dissipative structure was coined by Russian-Belgian physical chemist Ilya Prigogine, who was awarded the Nobel Prize in Chemistry in 1977 for his pioneering work on these structures, some of which rediscovered my research on what I call “enzyme waves.”
As chemist John Avery explains in his 2003 book Information Theory and Evolution, we find a presentation in which the phenomenon of life, including its origin and evolution, as well as human cultural evolution, has its basis in the background of thermodynamics, statistical mechanics, and information theory. The (apparent) paradox between the second law of thermodynamics and the high degree of order and complexity produced by living systems, according to Avery, has its resolution “in the information content of the Gibbs free energy that enters the biosphere from outside sources.” The process of natural selection responsible for such local increase in order may be mathematically derived directly from the expression of the second law equation for connected non-equilibrium open systems
Tim wrote:
Did you have a look at his book Modern Thermodynamics: From Heat Engines to Dissipative Structures (amazon)?
No. He has an infinite number of books, and I had trouble finding one that explained ‘Prigogine’s theorem’.
But I don’t think that there is a theorem…
Bummer! The paper by Oster and Desoer actually seems to prove some theorems. I just had a bit of trouble distilling them into mathematical prose and relating them to what other people called Tellegen’s theorem.
I should give it another try. There really are some nice ideas here.
This chapter explains this principle with 5 concrete systems (chemical reactions, thermal conduction and electrical circuits). Should fit snugly with the recent editions of This Week’s Finds.
Yes! I think I understand that entropy production is minimized by a large class of circuits in steady state. But I’m not quite sure what class this is! It includes circuits made solely of linear resistors, but maybe more. And I don’t know any theorem that explains this phenomenon starting from some other assumptions.
The paper by Oster and Desoer seems to have one… I’ve got to understand this paper better! This stuff is incredibly important; it’s ridiculous that I haven’t found a book that explains it well.
Just scanned a few books about non-equilibrium thermodynamics and found a precise and concise “proof” here:
p.51, 2.5.1 Minimum Entropy Production Principle.
Thanks! Great — this book is available online for us people whose institutions have a deal with Springer. So, I can read it now.
The authors say that the main assumptions behind Prigogine’s theorem are:
Let me try to distill the argument to its mathematical essence. Sorry, this won’t be very well motivated — I just want to jot it down quickly.
The state of a system is described by an -chain in some chain complex equipped with an inner product. We assume the rate of entropy production is
where the brackets are the inner product. Then taking the time derivative of both sides:
or using the adjoint of the operator :
A certain conservation law lets us write
for some linear operator . We thus get
In many cases the operator is negative definite, so that
In other words, the rate of entropy production decreases with the passage of time.
On the other hand, in a stationary state , so .
Then the authors say: “This result proves that that the total entropy production decreases in the course of time and that it reaches its minimum value in the stationary state.” Hmm — not sure I like that logic.
It seems the real meat of the argument is the proof that . And this idea — that entropy production decreases with the passage of time — is also what Oster and Desoer focus on. So it could be that this is the really interesting content of Prigogine’s theorem.
To wrap up (for now):
1. “Time-independent boundary conditions” are what let us do the “integration by parts” here: .
2. “Linear phenomenological laws”, “constant phenomenological coefficients” and “symmetric phenomenological coefficients” are what let us write the rate of entropy production as a quadratic form . I need to break this down into steps, but that’s roughly right.
3. Another crucial step is the equation . This again can be derived from smaller assumptions, but it’s worth noting that this is formally just a generalization of the heat equation.
JB:
In many cases the operator L is negative definite, so that . In other words, the rate of entropy production decreases with the passage of time. On the other hand, in a stationary state , so . Then the authors say: “This result proves that that the total entropy production P decreases in the course of time and that it reaches its minimum value in the stationary state.” Hmm — not sure I like that logic.
P is nonnegative and decreases with time, so it converges to a limit . Therefore converges to zero. Since L is negative definite, the formula for implies that converges to zero. This almost implies that converges; in concrete circumstances, usually more is known so that one can deduce convergence. The limit, if it exists, must be a stationary point – equilibrium.
Note that the assumptions 2.-3. are approximately satisfied in a system in its rest frame and close to equilibrium (and typically only then). If you want to have exactness (as your comment on the logic suggests), you need to take the nonlinear situation into account; then things are more complex but under natural and realistic assumptions one can bound the errors in the linearization. (Physicists generally ignore these fine points that cost significant formal effort without giving any extra insight into the physics.) 4. often follows from properties of the S-matrix when considering a nonequilibrium system close to equilibrium as a microscopic system. (See, e.g., Weinberg’s QFT book, Chapter 3.6.). 1. says that nothing enters or leaves the system.
Thus the whole derivation proves (to the satisfaction of the typical physicist) that a system close to equilibrium left alone will approach equilibrium.
Mathematical physicists can prove for many concrete systems that this is indeed the case rigorously, and even prove lower bounds on the speed of approach. This requires a concept called hypocoercivity, a property which the parabolic equations governing systems near equilibrium usually have.
Thanks! I understand that physicists get by with somewhat imprecise arguments, and I think that’s fine. But I’m always looking for places where mathematicians can turn these imprecise arguments into powerful, general theorems. Nonequilibrium thermodynamics is very important — large parts of everyday life are governed by it. Mathematicians should jump in and try to prove more and more general theorems delineating the situations in which 1) entropy production decreases and 2) entropy production is minimized in a stable equilibrium state. So thanks for giving some hints!
Thomas Riepe points out these remarks by Alain Connes:
I soon ran into Dennis Sullivan who used to go up to any newcomers, whatever their field or personality, and ask them questions. He asked questions that you could, superficially, think of as idiotic. But when you started thinking about them, you would soon realize that your answers showed you did not really understand what you were talking about. He has a kind of Socratic power which would push people into a corner, in order to try to understand what they were doing, and so unmask the misunderstandings everyone has. Because everyone talks about things without necessarily having cleaned out all the hidden corners. He has another remarkable quality; he can explain things you don’t know in an incredibly clear and lucid manner. It’s by discussing with Dennis that I learnt many of the concepts of differential geometry. He explained them by gestures, without a single formula. I was tremendously lucky to meet him, it forced me to realize that the field I was working in was limited, at least when you see it as tightly closed off. These discussions with Dennis pushed me outside my field, through a visual, oral dialogue.
This is part of an interview which you can read here:
21) An interview with Alain Connes, part II, by Catherine Goldstein and George Skandalis, Newsletter of the European Mathematical Society, March 2008, pp. 29-34.
He has a kind of Socratic power which would push people into a corner, in order to try to understand what they were doing, and so unmask the misunderstandings everyone has. Because everyone talks about things without necessarily having cleaned out all the hidden corners.
I can confirm this from personal experience. I once had the privilege (I mean that literally!) of being made clear how little I knew about my own work after trying to explain it to Professor Sullivan.
The chemist Jiahao Chen noted some relations between electrical circuits and some aspects of chemistry. I would like to understand these better. He wrote:
I am particularly piqued by your recent expositions on bond graphs, and your most recent exposition on bond graphs have finally seem to have touched base with something I have been trying to understand for a very long time. For my PhD work I worked on understanding the flow of electrical charge of atoms when they are bound together in molecules. It turns out that there is a very clean analogue between atomic voltages (electrical potentials) = and what we know in chemistry as electronegativity; also, there is an analogue for atomic capacitance = and what is known as chemical hardness (in the sense of the hard-soft acid-base principle in general chemistry). It has become clear in recent years that the accurate modeling of such charge transfer processes must necessarily take into account not just the charges on atoms, but the flows between them. Then atoms in molecules can be thought of as being voltage-capacitor pairs connected by some kind of network, exactly like an electrical circuit, and the charges can determined by an equation of the form
bond capacitance × charge transfer variables = pairs of voltage differences
I have described this construction in the following paper:
- J. Chen, D. Hundertmark and T. J. Martinez, A unified theoretical framework for fluctuating-charge models in atom-space and in bond-space, Journal of Chemical Physics 129 (2008), 214113. DOI: 10.1063/1.3021400. Also available as arXiv:0807.2174.
In this paper, I also reported the discovery that despite there being more charge transfer variables (bond variables) than charge variables (vertex variables), it is always possible to reformulate equations written in terms of charge transfer variables in terms of equations written into charges, and thus there is a non-obvious 1-1 mapping between these two sets of variables. That this is possible is a non-obvious consequence of Kirchhoff’s law, because electrostatic processes cannot lead to charge flow in a closed loop, and so combinations of bond variables like (1 → 2) + (2 → 3) + (3 → 1) must lie in the nullspace of the equation. Thus the working equation
capacitance × charge = transformed voltage
can be used instead, where the transformation applied to the voltages is a consequence of the topological relationship between the charge transfer variables and charge variables. This transformation turns out to be exactly the node branch matrix in the Oster and Desoer paper that was mentioned in your column! (p. 222)
I cannot believe that this is merely a coincidence, and certainly your recent exposition on bond graphs seems to be very relevant in a way that could be fruitful to think about. The obvious connection to draw is that the capacitance relation between charges and voltages is exactly one of the four types of 1-ports you have described, except that there are as many charges as there are atoms in the molecule. I don’t have a good background in algebraic topology, so I don’t entirely follow your discussion on chain complexes. Nevertheless I find this interesting that this stuff is somehow related to mundane chemical concepts like electronegativity and charge capacities of atoms, and I hope you would too.
Thanks,
Jiahao Chen · MIT Chemistry
In the above comment, is the energy of an ion and is its charge, or (up to a factor) its number of electrons. When Chen says is a measure of ‘hardness’, he’s referring to the Pearson acid base concept. This theory involves a distinction between ‘hard’ and ‘soft’ chemical species. ‘Hard’ ones are small and weakly polarizable, while ‘soft’ ones are big and strongly polarizable.
It seems that Jiahao Chen is hinting that certain “fluctuating-charge models” of chemical species are mathematically isomorphic to certain electrical circuits. I would like this very much, since I’m trying to expand the empire of isomorphic physical systems which I’ve been talking about in recent Weeks.
I plan to have a Skype conversation with Chen when I become less busy. But in the meantime, if anyone out there understands this kind of stuff and feels like explaining a bit of it, please post a comment!
To set a rough baseline for my ignorance: until yesterday I had never heard of the ‘Pearson acid base concept’, also known as the hard and soft acid and base theory. I knew there were various attempts to formalize the intuitive concepts of ‘acid’ and ‘base’….
Hendra Nurdin does quantum control theory at the College of Engineering and Computer Science at Australian National University. He works on networks of open quantum systems. In This Week’s Finds I’ve been focusing on classical systems, but most of what I’ve said so far has a quantum analogue. Here’s an example of a relevant paper:
If you look at this paper you’ll see a picture of a device with many input ports and output ports, which strongly suggests there’s a symmetric monoidal category at work here!
Dear John,
Your week294 starts with a statement, “I’m about to make a big career shift: I’ve been working on n-categories and fundamental physics, but in July I’m going to the Centre for Quantum Technologies in Singapore for a year, and I plan to think about technology and the global ecological crisis. I’ll probably keep thinking about the old stuff a bit, too.”
Does the last sentence mean you are going to keep maintaining This Week’s Finds on a more or less regular basis?
Tx, -Max
Max wrote:
Your week294 starts with a statement, “I’m about to make a big career shift…”
Actually that’s not how week294 starts. That’s what my homepage currently says.
I think the beginning of week293 answers your questions:
This column started with some vague dreams about -categories and physics. Thanks to a lot of smart youngsters — and a few smart oldsters — these dreams are now well on their way to becoming reality. They don’t need my help anymore! I need to find some new dreams. So, “week300” will be the last issue of This Week’s Finds in Mathematical Physics.
I still like learning things by explaining them. When I start work at the Centre for Quantum Technologies this summer, I’ll want to tell you about that. And I’ve realized that our little planet needs my help a lot more than the abstract structure of the universe does! The deep secrets of math and physics are endlessly engrossing — but they can wait, and other things can’t. So, I’m trying to learn more about ecology, economics, and technology. And I’d like to talk more about those.
So, I plan to start a new column. Not completely new, just a bit different from this. I’ll call it This Week’s Finds, and drop the “in Mathematical Physics”. That should be sufficiently vague that I can talk about whatever I want.
I’ll make some changes in format, too. For example, I won’t keep writing each issue in ASCII and putting it on the usenet newsgroups. Sorry, but that’s too much work.
I also want to start a new blog, since the -Category Cafe is not the optimal place for talking about things like the melting of Arctic ice. But I don’t know what to call this new blog — or where it should reside. Any suggestions? I may still talk about fancy math and physics now and then. Or even a lot. We’ll see. But if you want to learn about -categories, you don’t need me. There’s a lot to read these days.
Currently I’m thinking of doing my new blog on wordpress.com. One alternative is to do a Wordpress blog on my own website. Has anyone out there done this? I think that has some advantages, like better LaTeX abilities. It costs some money. But how hard is it to do? Suppose I’m an absolute klutz at UNIX…
I’m still trying to think up a good name for this new blog. Right now my favorite choice is a word that sounds cool but doesn’t mean much to most people. Other choices seem too specific (“Green Mathematics”), too erudite and hard to pronounce (“Techné Verte”), or too clichéd (“Pale Blue Dot”).
Suggestions, anyone?
->mathemateco.com
…but may be this exists already.
John wrote:
But how hard is it to do? Suppose I’m an absolute klutz at UNIX…
The obvious solution is of course “find someone who does it for you”. Team up with all other faculty staff menbers at the Centre for Quantum Technologies who would like to have a blog or already have one and get one grad student as administrator who handles all the techno stuff. (Or subcontract to India, it’s what the professionals would do :-)
Other choices seem too specific (“Green Mathematics”)…
Why is that too specific? Would ecomath be to specific, too, like my predecessor “sillypilly” suggests? If the topic of the blog is “abstract mathematics and physics applied to ecology”, that would seem to fit. For brainstorming, I would compile two lists, one with ecological terms, one with math and phys terms, and play around with combining these, like:
the sustainable propagator
green asymptotics
Greene propagators (duh, that’s too specific again :-)
future-proofs
the eco-eggheads (optionally enhanced by: “domain of convergence”)
etc.
these installation sites at wordpress are quite detailled:
http://codex.wordpress.org/Installing_WordPress#Things_to_Know_Before_Installing_WordPress
Tim writes:
The obvious solution is of course “find someone who does it for you”. Team up with all other faculty staff members at the Centre for Quantum Technologies who would like to have a blog or already have one and get one grad student as administrator who handles all the techno stuff.
Hmm. I’ll probably be blogging long after I return to UCR, and the technical support here is quite minimal (we’re broke), so I’m imagining doing something that I can do myself. I also don’t feel completely confident about freedom of speech for blogs based in Singaporean government-funded institutions.
Why is that too specific? If the topic of the blog is “abstract mathematics and physics applied to ecology”, that would seem to fit.
I’ll also want to talk about quantum technologies (that’ll be my job, after all) and various random subjects in math and science that happen to interest me that week. I really want to leave it quite wide open. This may diminish the blog’s effectiveness when it comes to organizing a community of people who want to solve practical problems… but the alternative is to have several blogs, and I’m not sure I want to compartmentalize things that way. I would like a number theorist who understands Riemann’s zeta function to read me talking about categorifying this function one day, and the next day see how this function plays a role in computing the energy emitted by a blackbody — a first small step towards understanding the temperature of the Earth. I want to lure ‘pure’ mathematicians into the great big world.
It’s a bit confusing, and I think only time will reveal the right path.
John wrote:
I’ll probably be blogging long after I return to UCR, and the technical support here is quite minimal (we’re broke), so I’m imagining doing something that I can do myself.
I’m probably thinking too complex: If you run an application on the web for even a small business there are a lot of things to take care of (availability, scalability, security, maintainability etc), that takes some time and is usually outsorced these days (by companies outside of academia). I guess all of this will be no concern to your new blog. And I did not anticipate that UCR is too broken to pay a few bucks to a student to take care of something like this, but with a little luck you will find all the help you need when asking for it on the blog itself (like you already did here).
I’ll also want to talk about quantum technologies (that’ll be my job, after all) and various random subjects in math and science that happen to interest me that week. I really want to leave it quite wide open.
Then I misunderstood your intentions by incorporating “ecologic terms” in the proposed names of the new blog, right?
I would like a number theorist who understands Riemann’s zeta function to read me talking about categorifying this function one day, and the next day see how this function plays a role in computing the energy emitted by a blackbody — a first small step towards understanding the temperature of the Earth.
That would be a more ambitious program than Hilbert’s quest to turn the “theorems” of physics to mathematical theorems…but given the wide open range of topics, maybe the simple name, connecting it with your other projects, would be a good choice:
Then I misunderstood your intentions by incorporating “ecologic terms” in the proposed names of the new blog, right?
If there were a way to do it that was 1) stunningly poetic, 2) instantly attractive, yet 3) didn’t seem to suggest that every blog entry would be about ecological issues, it might be good.
My wife Lisa is a poet and she’s good at naming things: she named the Lab and the (now sadly quiet) EUREKA wiki. She’s written books with much cooler titles than mine, like What Country and Knowing Words. But I still couldn’t get her to cough up a name for this blog that pleased me.
Every phrase with ‘green’ in it either seems a bit clichéd or a bit too specific ‘Green mathematics’ doesn’t sound clichéd to me, it still sounds like a shocking juxtaposition, but someday I bet it will catch on. But I don’t want the blog to scare away nonmathematicians! Bruce Sterling has already used ‘viridian’ and moved on. Lisa’s ‘Techné Verte’ sounds pretty cool, but you need to know a bit of classical Greek and French to pronounce it. ‘Techné’ is a very interesting word, by the way. But I can imagine lots of people stumbling over it while trying to pronounce it.
‘The This Week’s Finds Café’ is sort of nice, but ‘The This’ is quite awkward, and I think the ‘café’ concept works best for a group blog. Besides, I don’t want to sound like I’m competing with the -Category Café! Like a chef quitting and setting up his own restaurant across the street… not good.
Simply ‘This Week’s Finds’ would be fine if I decide that’s all that will be on this blog.
Anyway, I guess I should stew in my own indecision rather than dragging other people into it….
I run my own self-hosted Wordpress blog with LaTeX capabilities. I’d be more than happy helping you with any and all aspects of setting up and maintaining your own.
WOW! Thanks a million, Mikael!
A few questions to help me decide if this is the right choice for me:
1) Do you run your blog on a UNIX system? (I’m hoping you say “yes”.)
2) Do you need root access to get it to work? (I’m hoping you say “no”.)
3) Do you need the blog to be self-hosted to get full-fledged LaTeX capabilities? For example: during the -Café’s brief stay on wordpress.com, it seemed that we could not get $$ $$ to produce displayed equations unless we switched to a self-hosted Wordpress blog. I’m curious about this sort of thing.
4) What’s the technically hardest part of running a self-hosted Wordpress blog?
If you go with Wordpress, I’m not sure if there is a huge advantage for going “self hosted”. For simple LaTeX, a hosted blog is fine. My blog is hosted by Wordpress and I have no problem with LaTeX.
You can even use your own domain and be hosted on Wordpress if you don’t like seeing “wordpress.com” in the url.
Eric wrote:
My blog is hosted by Wordpress and I have no problem with LaTeX.
Now I remember our problem at the Wordpress -Café. People posting comments were unable to create ‘displayed’ equations — that is, equations that are centered in the page.
Do you know anything about that? It’s a mild nuisance, but perhaps a warning of many more mild nuisances to come.
You can even use your own domain and be hosted on Wordpress if you don’t like seeing “wordpress.com” in the url.
Kewl!
How does that work? I’ll admit, I don’t like the idea of my blog being such a blatant advertisement for someone else’s company.
LaTeX in comments are fine, but I’m not sure you can center them. That is being a little nit picky though :)
Have a look.
Eric wrote:
That is being a little nit picky though :)
True, but it suggests they could be implementing a very limited form of LaTeX, which makes me wonder what the limitations are, and what more you get from plugins like this and this.
These plugins seem to only work if you pay to install a Wordpress blog on your own site. But it’s not obvious that they really do more than what you can now get for free.
I could help run some tests. Give me some LaTeX and I’ll see how it comes out on Wordpress. Diagrams should come out fine as arrays, etc.
PS: You would be doing me a humongous favor if you can help me escape my mental trap at the n-Forum. I’ve been going in circles for days…
Forgot you already had a Wordpress playground :)
John wrote (emphasis mine):
These plugins seem to only work if you pay to install a Wordpress blog on your own site.
At what point do you need to pay? The implication in this sentence is that Wordpress charges you for use of its software. That’s certainly not true:
Everything you see here, from the documentation to the code itself, was created by and for the community. WordPress is an Open Source project, which means there are hundreds of people all over the world working on it. (More than most commercial platforms.) It also means you are free to use it for anything from your cat’s home page to a Fortune 500 web site without paying anyone a license fee and a number of other important freedoms.
(Quote taken from http://wordpress.org/about/)
Of course, if you don’t have access to a PHP+MySQL system, say via your university, then you need to pay for one, but that’s paying for the hosting not for the wordpress installation itself.
And if you yourself don’t have a PHP+MySQL system (or don’t quite know what that means!), I’m sure you could find someone with a bit of bandwidth to spare who would be willing to host it for you! After all, the kudos of hosting the new Baez Blog would be quite something …
1) I run it on a Linux system I administer myself.
2) Having root, or at least having a root who’ll help you, will help getting things set up Just Right.
3) I do not know, right now, about hooking up to $ $ / $$ $$ for LaTeX capability; I’m sure it’s mostly a matter of tweaking the right PHP scripts to do the right thing throughout. On my own blog, I use [tex] [/tex] to delimit actual TeX data, and I go the generate-images route for display. However, on the (now defunct) Infinity blog I tried launching a while back, I had taken care to make things work with MathML using Distler’s plugins.
4) Technically hardest about running a self-hosted blog? Keeping the computer that hosts it secure and unhacked. Technically hardest about running a self-hosted blog without any quirks that annoy you? Understanding and tweaking all the PHP code you use until it does what you want.
In this comment over at the nForum, Andrew has announced he’s developed a plugin for Wordpress, which will allow seamless (even copy paste) use of itex (the flavor of TeX used on the nCafe, nLab, and nForum).
If I understand the implications, it means all the nice rending available here and the nLab is now available as a Wordpress plugin.
PS: Andrew rocks :)
PPS: I suggest someone elevate this announcement to a new blog entry.
PS: We are also discussing opening up the scope of the n-Forum to become a more general discussion forum on any reasonable scientific areas of interest. This involves blogs as well, so if anyone might be remotely considering starting a new blog *cough* in the near future, they might consider seeing what can be done to keep everything in the family.
Through the magic of CSS, it is pretty easy to modify the look and feel.
As Eric has already “announced” this for me, I figured I may as well make a test site to showcase it:
http://www.math.ntnu.no/~stacey/Vanilla/WPMathML
If anyone wants to help test it “from the other side” (ie with test posts), please email me.
All Wordpress math bloggers rejoice. This is completely and totally awesome. Thank you Andrew!
All this new development Andrew is delivering is very exciting. One thing which makes me uncomfortable with nCafe is the lack of meaningful cut-and-paste, as the source code of the most entries is not readily available, so quoting math means retyping math (and for some formulas one does not know how in this environ). I hope the availability of the source for everybody is among top priorities of the new nice merger of iTeX with WordPress…
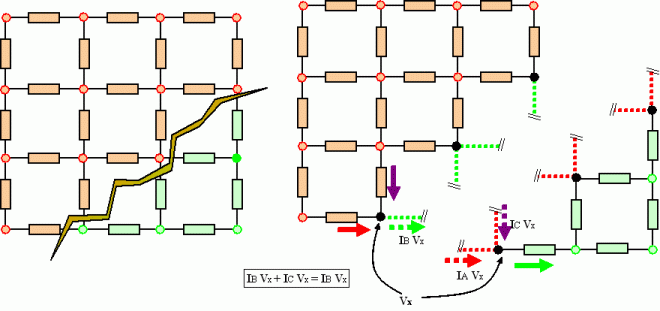
Re: This Week’s Finds in Mathematical Physics (Week 294)
Is there a reason, by the way, why you need to only add meshes until things are contractible? It seems like an artificial requirement, and considering, say, circuit design for etched circuitboards with vias, not entirely realistic.
Why not just add all meshes, and allow for non-trivial second degree homology and cohomology? It won’t hurt the exactness in degree 1…