In week293 of This Week’s Finds, catch up on recent papers and books about -categories. Hear about last weekend’s Conference on the Mathematics of Environmental Sustainability and Green Technology at Harvey Mudd College. And learn how to think of networks of resistors as chain complexes which are also morphisms in a category.
Posted at February 6, 2010 7:43 AM UTCTrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2166
Whoops! Fixed.
This book is 925 pages long! Luckily, Lurie writes well.
Yes. On top of everything, it is a very nice exposition.
But still, since that number of pages is always emphasized so much, some words on it:
I hope nobody thinks that a math book should be read like a crime story, first page first, last page last. You all read stuff on the internet each day. The number of pages on the internet is enormous – but nobody is scared away by that . Same holds for texts on math. If they have a table of contents, then they are all the same size: one page per page.
In fact, as I said before, one good way to read HTT is to read it backwards . Start with the appendix. One of the best surveys of model category theory that is available. Then notice in particular the very last three propositions on the very last two pages of the text. This recalls Dugger’s theorem on combinatorial model categories. You can read the whole of higher topos theory in the book as the evident way of finding an intrinsic categorical model-independent formulation of Dugger’s theorem.
Coming back to the one-page-per-page remark: tf you don’t read one book of 900 pages, you will probably in the same time read 2 books and 20 articles of a total of 900 pages. I take it that we all read at a given speed continuously anyway, not having the idea that soon we have read everything and will stop until something new finally appears. From that perspective it is useful to know: reading 50 pages in Lurie saves you, I claim, from reading some order of magnitude higher number of pages on similar content. He makes it all become crystal clear.
So, you save time by reading Lurie. You can safely stop reading many other things, if you do. That’s a huge gain in time and effort!
Urs, this seems like very good advice:
In fact, as I said before, one good way to read HTT is to read it backwards . Start with the appendix. One of the best surveys of model category theory that is available. Then notice in particular the very last three propositions on the very last two pages of the text. This recalls Dugger’s theorem on combinatorial model categories. You can read the whole of higher topos theory in the book as the evident way of finding an intrinsic categorical model-independent formulation of Dugger’s theorem.
I have to plead ignorance: my knowledge or understanding of model category theory is still very shallow, I would say. So my question would be: why should I care that this is what the book is about? That is, why is Dugger’s theorem to be considered a central and powerful result; what are its important applications?
Duggers theorem identifies the notion of combinatorial model category as precisely that type of model category that is obtainable as a left Bousfield localization of the global projective model category of simplicial presheaves.
With a little experience on model categories, one sees that this statement is trying to say something very basic about -categories:
the global projective model structure on simplicial presheaves looks like it should be a model for -categories of -presheaves .
the operation of left Bousfield localization looks like a model for reflective -subcategories .
So one might expect that the intrinsic meaning of Dugger’s theorem is that it characterizes models precisely for reflective -subcategories of -categories of -presheaves
One of Lurie’s central theorems of higher topos theory is that this expectation is precisely right: combinatorial model categories model precisely the locally presentable -categories.
This is the crucial first ingredient for higher topos theory. Because among all presentable -categories, of course we want to define the -categories of -sheaves as precisely the left exact reflective embeddings
And this was of course Dugger’s starting point, originally: Dugger had observes that the local Heller-Joyal-Jardine model structure on simplicial preshheaves, which felt like it should model -stacks, is a certain left Bousfield localization of the global structure of simplicial presheaves.
Lurie proves that this is also exactly right. That means, to some extent, Lurie’s book shows that -topos theory had been known already in terms of certain generators-and-relations presentations that people had guessed over the years. Lurie’s book provides an intrinsic category-theoretic picture that is modeled by these models.
An exposition of this story is at models for -stack -toposes.
By the way, there is also the page
Seminar on -categories and -stacks
that means to sketch the route starting with Dugger’s theorem into higher topos theory.
(This is under construction. But might already be useful. Comments are welcome.)
Do I have to care about model categories if I'm already interested in (∞,1)-categories for their own sake?
Do I have to care about model categories if I’m already interested in (∞,1)-categories for their own sake?
No. You don’t have to. It’s a calculational tool. If you can do without that tool, that’s fine.
By Dugger’s theorem, a model category presentation is like a generators-and-relations presentation of a category. You don’t have to care about generators-and-relations presentations of cvategories when you are interested in category theory. But sometimes its a useful tool for talking about categories.
Much stuff these days is done with -categories without falling back to model presentations.
“when light passes from light to glass”—second “light” should be “air”.
This was a very nice “Week”.
Thanks! Fixed!
John, can I recommend that solar would make more sense with Stirling Engines since this does not require fancy and
expensive clean rooms, and is more efficient. Off hand, if one can make a weed wacker engine then one can make a Stirling engine.
This point was mentioned by a member of the audience. I would like to learn more about the comparative advantages of photovoltaics versus solar-powered heat engines. But the speaker, Harry Atwater, was an expert on photovoltaics, so that’s what he talked about.
For those interested in thermodynamics, it’s fun to read about Stirling engines.
Alpha type:
Beta type:
Red is hot, blue is cold. Gas expands when it touches the hot stuff, contracts when it touches the cold stuff. Stare at them and figure out how they work.
It is not so easy to make a solar Stirling engine that beats a photovoltaic cell in efficiency. If you could make a 600’C heat source from solar heat, you could run a Carnot engine from that with an efficiency of 50%. Most practical engines run at less than half the Carnot effiency, which puts you back at 25%.
But making 600’C heat from solar is not so easy. You can do it with mirrors (Heliostats). By the time you have gone through that trouble, you will probably replace the Stirling engine by a steam turbine.
Perhaps if you don’t care about efficiency (solar is free), and just go for a really cheap and simple device, there might be some hope for Stirlling engines. I think about it sometimes, but if it were easy, I would have had one on my roof already.
Gerard
Gerard wrote:
Perhaps if you don’t care about efficiency (solar is free), and just go for a really cheap and simple device, there might be some hope for Stirling engines.
Right. The real issue in solar power (or any other sort of power) is not efficiency in the technical sense of what percent of the input energy gets converted to electricity. It’s much more complicated economic calculation, which depends on the local conditions. Perhaps there are relatively poor places that get a lot of sun, where inefficient solar units that are cheap to make could be useful. These places surely won’t be buying top-efficiency photovoltaics!
Maybe you’re right that a Stirling engine together with mirrors is too complicated and inefficient to have a nice market niche. I have no idea.
inefficient solar units that are cheap to make
Like solar cookers?
a nice market niche
(not to be confused with a nice niche market!)
I’ve also been dragged into writing my first paper related to Global Warming, by professional economists interested in analytical and simulation models of the derivatives (options) markets built on top of emission credits. That is, not modeling Climate Change, nor modeling the modelers, but modeling the investors who are modeling the modelers, using Mathematical Economics and Mathematical Biology. Bad investors are Prey to good investor Predators, hence there are cycles and, as shown in 1988, chaotic states existing in the Lotke-Volterra model.
Historic times with the last TWF in Mathematical Physics just months away! It feels unsettling like when an older sibling moves out from the family home.
I just read a newspaper article on the not so aptly named rare earth metals. It seems that China produces 97% of global supplies. Baotou is the place to be.
Historic times with the last TWF in Mathematical Physics just months away!
Yeah, I remember when you wrote
But no matter what happens, I’ll probably keep wanting to write This Week’s Finds, and posting that here.
Sad news! But I'm sure that you'll still be posting interesting commentary some place or another.
But I'm sure that you’ll still be posting interesting commentary some place or another.
(I wrote that wrong; it implies that I'm estimating, while in fact you said that you would. And it doesn't contradict the quotation above either; that just didn't mean what I thought it did!)
I thought about it a while and decided I won’t have the energy to run ‘This Week’s Finds in Mathematical Physics’ in its old form while exploring new territory. For example, I may want to start a blog that’s devoted to collecting and presenting clear, accurate information on climate change, economics, ecology, and related technologies. Ideally other people would join in, because it’s too big a job for any one person! But then talking with these other people will absorb a lot of energy and time.
(Indeed, the reason I say I ‘may’ want to do this is that I sometimes quail at the prospect!)
On the other hand, I still want to be able to write about quark-gluon plasmas, the octonions, or other esoteric mathematical physics topics if I happen to learn anything interesting about those.
So, it’s a tricky decision — but right now it seems like writing a column with the noncommittal title ‘This Week’s Finds’ is the best way to deal with this.
I still need to envisage the target audience, so I can try to write in a way that most of them will enjoy, mostly, most of the time.
If it’s going to have any effect on the big issues facing our planet, it’ll have to be readable by people without math or physics Ph.D’s. But I want to avoid attracting a huge audience of argumentative idiots.
What do people think about the idea of a blog where you need a password to post comments? Is this dumb?
My opinion is that making readers sign up in order to post comments makes sense only after you have readers. It is difficult enough to start a new community without putting up barbed wired fences right at the beginning.
When you write a new article and you get one legitimate comment and one spam gets through the spam blocker, just delete the spam rather than punish the legitimate commentor. Once you get to the point, and you probably will eventually, where you find yourself spending time combating spam that you’d rather use writing articles, then you put up the password protection. At that point, i.e. once spam is a clear problem to legitimate readers, then people will care enough that they won’t mind signing up for an account.
This is the pattern I’ve seen over and over. Develop a community without passwords, while letting the spam blockers do their job. Once some spam gets through, manually delete it because, in the beginning the community will be small and this will be manageable. When the community grows to the point where spam blockers are letting too much spam in and manually dealing with it becomes formidable, THEN you put up password protection.
Basically, forcing people to create an account is a great way to fight spam, but only after the community is solidly established and spam is a clear problem to everyone.
That makes sense, Eric.
An alternative filter to requiring sign in to prevent spambots is to include a minimal Turing test question appropriate to the topic, that anybody with a real reason to post will know, and even a wander-in person can look up. Human spammers who make an effort will still be able to get through, but the average spambot won’t. Only comments that include a correct answer on the form get posted.
I helped with one of these for a yeast genomics site that had a couple of fill in the blank questions, something like:
Questions to demonstrate you’re a biologist, not a spambot:
G, A, T, and ___
James Watson and Francis ________
Its a bit extra work, but the person doesn’t have to create and remember a password, etc.
What do people think about the idea of a blog where you need a password to post comments? Is this dumb?
Better than deleting comments by hand or by blocking specific IP addresses.
I’ll chip in with one obvious idea: e-mail the authors of blogs like Robert Rapier’s energy blog and David McKay’s “Without Hot Air” blog and ask them about the issues relating to “undesired comments”.
I read a lot about possible future reduced energy availability and I think the issues coming up there will be the same as for environmental stuff (with which there is some overlap). I don’t think the taxing issue will be genuine spam posts. The issue will be that on environmental issues (amongst others) that you don’t face much at the cafe is that, for a variety of good and bad reasons, people believe strongly in their viewpoint on various issues and will post chains of replies arguing that the assumptions, or the choice of measurement, or the logic, or that you’re comparing apples-to-oranges, etc. These are posted by people who are undoubtedly sincere, and could sometimes be right. (On energy it’s often the case that I don’t have the detailed knowledge to spot who’s making the mistake.) So they aren’t spam coments but they are potentially very time consuming to respond to meaningfully, and it can be difficult to stop it taking on a personal edge. I’d say your most important task is to figure out a policy (for your own sereneness) for how you’re going to deal with a situation where you think a commenter is wrong but after a couple of comments exchanges it’s clear neither of you will persuade the other of their own analysis.
Anyway I hope you acheive both influence and equally importantly personal happiness in this endeavour.
Bane wrote:
I don’t think the taxing issue will be genuine spam posts.
Right. I think Eric was using the word ‘spam’ in an extremely loose sense.
I’d say your most important task is to figure out a policy (for your own sereneness) for how you’re going to deal with a situation where you think a commenter is wrong but after a couple of comments exchanges it’s clear neither of you will persuade the other of their own analysis.
Right.
Actually, having spent years moderating sci.physics.research, I’ve developed an incredible ability to let the other guy have the last word. I’m actually more worried about commenters arguing endlessly with each other.
I’ve even considered a blog where all issues of policy — ‘what we should do’ — are off limits, and only matters of fact can be discussed. It would be an interesting experiment. But I’m not sure it’d achieve what I’m after.
It’s also quite possible that the world does not need another blogger! Maybe I should simply quit blogging, post This Week’s Finds on my website, and hope that people with truly important comments will take the trouble to email me.
Hmm, this is a potentially revolutionary concept.
I wrote a web page myself on global energy recently.
But my web page on geometry gets about 5X more hits per day.
I don’t know why this is. Potentially a lot more people could be interested in global energy solutions than in something like octonions. Another question is, should I care about the number of hits per day?
I guess there is no easy answer to the question of what to spend you time on.
Gerard
“There’s a lot less sea ice in the Antarctic, mainly in the Wedell Sea, and there it seems to be growing, maybe due to increased precipitation.”
Is there a typo here? Anyway, isn’t southern hemisphere ice extent currently very close to average?
I meant there’s a lot less sea ice in the Antarctic than the Arctic — but most of that ice is in the Weddell Sea. And, while the ice is shrinking rapidly in the Arctic, it’s growing slightly in the Antarctic.
I can imagine all sorts of misinterpretations of the lousy sentence you quoted — I assume you’re not complaining about my spellling of ‘Weddell’. I’ll improve it.
In connection with photovoltaics, it seems that collecting photon-conversion energy in excess of the bandgap may be possible (harnessing “hot electrons” appears to be the terminogy), allowing it to exceed the Shockley limit, as discussed here. (They claim up to 67 percent efficiency, but in the light of the wikipedia page saying that 50 percent of incoming solar radiation has energy below the minimum bandgap, I presume it must mean 67 percent of the energy in photons with energy above the bandgap.)
Looking at the homepages linked in that article, there are some lists of academic papers whose titles hint they may be discussing this stuff in technical detail, but I don’t have access to any of them so I won’t guess.
I like the n-Categorization of the flows in networks. Of course, you sneakily pretend at first that this is about finite directed graphs, as in The Ford-Fulkerson algorithm (named for L. R. Ford, Jr. and D. R. Fulkerson) which computes the maximum flow in a flow network. It was published in 1956. But two directions to generalize (as you know well) are to locally finite graphs; and to hyperflows along hyperpaths in hypergraphs.
about solar applications of Stirling Engines, there was a site I ran across two years ago, complete with very fancy animations, and mentioned that a deep space probe used Stirling - and may still be working out there. infinia, and there might be others. The one i remember had patent applications on it with all kinds of engineering and performance stuff.
A detailed treatment of the relation of circuits to chain complexes along the lines of your discussion can also be found in chapter 12 and beyond in “A Course in Mathematics for Students of Physics,” by Bamberg and Sternberg (Cambridge Press, 1990).
It seems like there should be one more, perhaps overly complicating, connection to be made in the hierarchy of chain complexes. In real circuits (especially at higher frequencies), the branches aren’t the only thing that can connect parts of a circuit together. Farady-law induction can provide electromotive forces to move charges in one mesh that should be proportional to *changes* in current in other meshes. The proportionality factors that enter in here are called “mutual inductances,” and this is the basis for transformers. (They’re more than meets the eye!)
I think such through-space influences are called “flux linkages.” Microwave and radio-frequency circuit designers have to take them into account carefully. As the branches of the circuit connect nodes (unit vectors in the space of zero-chains?), it seems like a vector space generated by flux linkages should somehow formally connect the meshes, and be subject to a boundary operator.
Garett wrote:
A detailed treatment of the relation of circuits to chain complexes along the lines of your discussion can also be found in chapter 12 and beyond in A Course in Mathematics for Students of Physics, by Bamberg and Sternberg (Cambridge Press, 1990).
Thanks! This chain-complex-and-electrical-circuit stuff is well known, but I was having trouble finding a really good reference. I’ve heard that Raoul Bott discovered it. Shlomo Sternberg taught at the same school as Bott, so I wouldn’t be surprised if that’s how he got turned on to this stuff.
I like A Course in Mathematics for Students of Physics, and recommend it to physicists trying to learn math, but I don’t own it. I suspect that a very detailed treatment of electrical circuits can be found here:
But I don’t have this at hand, either.
It seems like there should be one more, perhaps overly complicating, connection to be made in the hierarchy of chain complexes. In real circuits (especially at higher frequencies), the branches aren’t the only thing that can connect parts of a circuit together. Faraday-law induction can provide electromotive forces to move charges in one mesh that should be proportional to changes in current in other meshes.
I definitely plan to generalize my discussion from circuits made from resistors to linear circuits made from linear resistors, capacitors, inductors, transformers and gyrators. The issues of time-dependence, Laplace and Fourier transforms, and complex analysis show up at that stage. But when you start talking about one mesh interacting with another distant mesh thanks to electromagnetic radiation, you’re going one step further.
Past a certain point, one might as well break down and talk about the full-fledged Maxwell’s equations. But you’ve got a good point — there’s got to be a useful intermediate regime where we still think about a circuit, but allow linear interactions between distant meshes.
You’re suggesting that we could do this by promoting our chain complex to a 4-term complex
That’s the size of complex you’d get from a finite-element model of 3d space! Or in math jargon: a 3d cell complex.
One thing I like about electric circuit models is that you can continuously refine them. For example, you start with an ideal voltage source. If you want to model that it does not give an infinite current when you short-circuit it, you can put in an internal resistance. Then, if you want to take into account that it behaves different for high frequency, you can put in various “parasitic capacitances” or “parasitic inductances”. “Parasitic” refers to the fact that you usually don’t like them, and did not put them in as components, but unfortunately, they are there. Ultimately, you want to be able to refine the circuit till you end up with the Maxwell equations.
Here is an animation of an electromagnetic standing wave in a circuit:
The magnitude of the magnetic field is animated as rate of rotation of the mesh inductors, the magnitude of electric field is animated as the size of the colored bars attached to the capacitors.
You could couple 2 different current meshes to a single mesh inductance. This is essentially saying that the 2 meshes are so tightly coupled that you don’t include the coupling explicitly anymore. Which is in principle the same as other forms of discretisation.
Maybe it would be fun to create animations of the electromagnetic fields of various example situations. But this takes time…
Gerard
Quoth Gerard Westendorp:
Maybe it would be fun to create animations of the electromagnetic fields of various example situations.
Or you could build a mechanical model of the electric field out of rubber bands, rotating rings and ratchets, like Fitzgerald did! I’d love to see one of those.
Gerard wrote:
One thing I like about electric circuit models is that you can continuously refine them.
Yes, indeed. This should be formalized using what mathematicians call ‘deformation theory’. The idea is that a given model can be fit into a smoothly varying family of models such that .
If we restrict attention to linear models, just for convenience, we could try something like this for starters. A model is a cochain complex with a quadratic form on the space of -chains mod exact -cochains:
This quadratic form is either the ‘energy’ or ‘action’ depending on whether we’re taking a space or spacetime viewpoint. Maxwell’s equations and linear electrical circuits fit nicely into this paradigm.
Then the idea is define a concept of isomorphism between such models, with a slightly unusual property: any cochain complex equipped with counts as isomorphic to the trivial cochain complex. In other words: if you ain’t got no energy (or action), you might as well not exist.
Then we can try to define a moduli space, or more precisely a moduli stack, of such models, in order to do deformation theory.
(Sorry that this math sounds so fancy, but something like this is really going on.)
Then we can talk about ‘deforming’ a perfectly conductive wire into a wire with a bit of resistance, or deforming a circuit by adding interactions between distant meshes, as Garett suggested…. and so on.
John wrote:
I’ve heard that Raoul Bott discovered it. Shlomo Sternberg taught at the same school as Bott, so I wouldn’t be surprised if that’s how he got turned on to this stuff. I suspect that a very detailed treatment of electrical circuits can be found here:
P. W. Gross and P. Robert Kotiuga, Electromagnetic Theory and Computation: A Topological Approach, Cambridge University Press, 2004.
There was an early reference to Bott’s work on this blog - which I can no longer find. (The search function protests i have one already underway and should wait!)
There’s considerable history including autobiography about Bott on the web and soon there will be more in a book from a conference organized by Kotiuga:
A Celebration of Raoul Bott’s Legacy in Mathematics
including several personal reminiscences.
Hold on a second…
What you write as is what I would have written as . Since you will eventually relate this to Maxwell anyway, I might suggest writing
so that Kirchov’s voltage law is really
This is more in line with circuit theory anyway since the voltage difference across an element is given by
The real fun will come when you extrude these circuits into time :)
I’m not really planning to relate this stuff to Maxwell’s equations, though I’d do so if I were trying to write the definitive treatment of how all physical concepts fit together in a beautiful whole. 
I thought electrical engineers commonly used for the voltage across a resistor. That’s why I used the letter as I did. If I’d wanted to remain consistent with the notation of previous weeks, I’d have used ! If I’d wanted to follow bond graph notation, I would have used , for ‘effort’. It’s essentially hopeless trying to get a unified notation for all of physics and engineering that pleases everyone.
The direction I’m going next is a bit different: Tellegen’s theorem, and then Prigogine’s theorem, as discussed here.
Fair enough :)
By the way, I’m really excited about following what you are doing here.
Overpopulation is the fundamental underlying driving factor in nearly all of our environmental problems and a good many of our political disputes. If you think it through slowly and carefully the causal relationships are very clear.
The overpopulation issue is largely avoided by political leaders because it is definitely not PC (very unpopular) and it is going to be incredibly difficult to solve on our own. If we fail to do so, nature will apply the necessary corrective, but we will find that exceedingly painful.
The Center For Biological Diversity has declared Feb 2010 as a “Speak Out Against Overpopulation” month. I suggest that you give this issue some very serious thought. If you agree that it is our most important goal, and sine qua non, in terms of “saving the planet”, then I urge you to help rally the troops to this unpopular cause. Without a serious commitment to solving the overpopulation problem, many noble environmental efforts will be ineffective, and unfortunately, pointless.
what about the decrease in birth rate `due’ to affluence?
Jim wrote:
what about the decrease in birth rate ‘due’ to affluence?
It’s a hugely important thing, and many consider it the answer to the population problem.
I read an article in Foreign Affairs yesterday claiming that Europe has an underpopulation problem! But this was written by someone who seems to think endless ‘economic growth’ is good, where economic growth is defined in a rather naive way.
The hard part is getting most of the world to a high level of affluence without destroying the planet in the meantime. I don’t know if it’s true, or precisely what it means, but the Global Footprint Network claims that if everyone lived like an American, we’d need 5 Earths to make that sustainable. The calculation is supposed to proceed like this. Regardless of the details, I think we need to bring the world to ‘affluence’ in a different way than the US and Europe got there.
John Baez wrote:
…Europe has an underpopulation problem!
In Germany the situation of a shrinking and aging population has it’s own name, it’s simply called the “demographic problem”. As an incentive, the last government introduced “parent time”, where mother or father can stay at home, take care of a newborn, and get paid a certain fraction of the last salary, by the government, while the employer has to ensure that the parent can return to the job later.
IMHO it would be more effective to make immigration easier, but unlike the USA most European countries don’t consider themselves to be “immigration countries” (which is a bit odd, because here in Munich almost 25% of the population are foreign-born).
what about the decrease in birth rate due to affluence?
From what I know, the most important factor is education, not necessarily wealth.
The “5 Earths” article is hardly new, I remember hearing about this for all my life - so while I don’t know how accurate this estimation is, I’m clearly used to this number.
In terms of sustainability “footprints”, I find this analogy to the little worlds in the Little Prince charming: “My Little World (And Yours Too)”. The author, Michael Tobis, has a blog on sustainability, climate change, and the conflicts between economic assumptions of perpetual growth and a world with finite resources.
what about the decrease in birth rate ‘due’ to affluence?
I'm interested in the decrease in birth rate correlated with (‘due’ to) women's rights. Wealthy countries with restrictive immigration policies sometimes crack down on women's rights when their population falls. This is one reason why immigrants' rights are also important, although a parochial approach to population control might suggest otherwise.
I recently read Three Cups of Tea and its sequel, Stones Into Schools. They are a personal account of the founding and work of the Central Asia Institute and its efforts to build schools in rural Pakistan and Afghanistan, mostly for girls who otherwise have no access to education. They hope that the indirect benefits of educated women will include better standard of living for women, reduced population growth, better community health, more widespread education of future generations of children, and less terrorism.
I’ve read only 3 cups of tea and look forward to Stones into schools, so I’ll add just - it’s not only a worthy story but a great read.
To a large extent excessive birth rates are driven by very poor living conditions. Under these conditions many children will not survive and so one needs a large family in the hope that some will survive.
In order to get large populations to decrease their birth rates, it is necessary to raise the standard of living to acceptable levels, especially regarding mortality rates, health care, economic stability, control of violence, educational opportunities.
If this could be done then people do not have the pressure to have large families. To the contrary in a stable environment with an acceptable standard of living, small families with intensive nuturing are favored.
Enlightened self-interest would encourage us to stop blowing each other up and ignoring extreme poverty. Rather we should be encouraged to strive for global stability.
Admittedly, much easier to say than to do. But at least we could start thinking about some goals for reducing poverty and making big educational efforts.
RLO
The Population Bomb came out in 1968
and the population was 3.5 billion.
Now it is double.
That would seem to show that a whole
lot of talk has had no effect.
Hello Joel,
Well, the results so far do not bode well for the human species, much to the delight of numerous other primitive species.
However, we must bear in mind that Paul Erlich was somewhat of a lone voice in 1968. As the effects of overpopulation begin to make us more miserable, the need to actually do something about lowering birth rates might get more press and attention. Certainly some countries have recognized the problem and have tried to encourage their citizens to change their cultural norms.
A serious concern is the lag time between instituting more sustainable population dynamics and seeing actual decreases in the world population. If I remember my E.O. Wilson correctly, there is a big time lag and if we do not act soon, then a certain amount of disaster is unavoidable.
The same time lag problem is true of global environmental pollution, water scarcity, etc.
If we want rational controlled change, then we need to get on with it. The alternative is chaotic uncontrolled change. One is reminded of the frightening scenarios presented in the movie “Children of Men”, based on a book of the same name by P.D. James. A very scary vision of a future that is not inconceivable.
Perhaps it is time to put our greed, pessimism, cynicism, etc. aside and do something - starting with speaking out loud and clear to our elected leaders. Political aspirants should give us their views of the population bomb before we vote for anyone.
RLO
At the risk of being identified as a barely closeted “crackpot”, I am desperately seeking open-minded responses to the following.
http://arxiv.org/ftp/arxiv/papers/1002/1002.1078.pdf
The standard response is that the statistical significance is in doubt, given the size of the particle “zoo”, but no one has actually demonstrated any lack of statistical significance. To me it seems likely that this criticism is a red herring that merely gives the reader an excuse to ignore the upsetting results.
I promise not to belabor the issue, other to say that I am shocked by the lack of interest in what, at face value, appears to be an extraordinary result. Perhaps the problem is that it strongly suggests that the current paradigm has major errors in its assumptions.
Well, same as it ever was. No?
RLO
You are explaining the Chew–Frautschi plot along Regge trajectories?
Without necessarily going into whether your theory is sound, I'd still like to hear what the physicists here have to say about that in general. Is this a statistically significant correlation? Do we have an orthodox explanation for it?
I had never heard of this until I started following up your comment; it seems to be a subject that attracts crackpots (not that this means that you are one, of course), and I can't find a straight answer using only Google.
Can you recompile the pdf and include fonts? For me, many of the symbols are blank in the version you pointed to.
It seems that the big disappointment was that solar did not follow the PC revolution. Living in a city apartment
provides no opportunity and much of the population is out of that loop. So it is difficult to harness the market to drive
the refinement of solar tech. For those who would put something on the roof, it is simply unaffordable without loans. If PCs cost 20 grand there would be no computer
revolution. The main reason to consider heat engines and avoid heliostats or parabolic troughs would be to hope for
something useful and affordable - which dictates conventional tech. Its a bit strange that there are programs to optimize the daylights out of processors but not heat-engine + alternators. Or am I mistaken ?
See the latest issue of The Nation for article on `gray power’, e.g. capture of `waste energy’ from
manufacturing plants etc
I thought ‘gray power’ referred to the political pressure of gray haired opinion in the USA! (It could also be obtained by recycling the ‘hot air’ we produce.)
John said: ‘So, “week300” will be the last issue of This Week’s Finds in Mathematical Physics.’
Noooooooooooo!!!!!!!!!!!!!!!!!!!!!!!!!!
Say it’s not true!!!!!!
That’s an era I was hoping wouldn’t end.
– Doug
Don’t be too heart broken. He’s not disappearing. I’m looking forward to the new “This Week’s Finds” :)
In your exposition of Kirchhoff’s laws, you start out identifying the current as a 1-chain and the voltage as a 1-cochain , and demonstrate that Kirchhoff’s laws require these to be a 1-cycle and a 1-cocycle, respectively, which gives us the mesh current and the electrostatic potential. Then, however, you state that the formula is a transformation from a 1-cochain to a 1-chain, and write .
But takes the current - a 1-chain - and gives you a voltage - a 1-cochain, right? So from the start of your discussion of the resistance and onwards, the dualizations should all be switched around, so that we get and the inner product is on 1-chains, such that yields the isomorphism between and ?
[John Baez: I guess you’re right! Thanks, I’ll fix it up. By the way, electrical circuit theorists like to have convenient names both for this isomorphism and its inverse: in time-dependent circuits they call the generalization of resistance the impedance, , and they call its inverse the admittance, . So then we have and . And now you know electrical circuit theory from to .
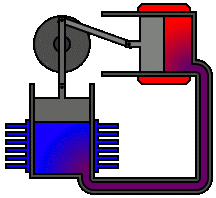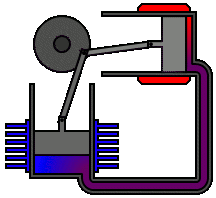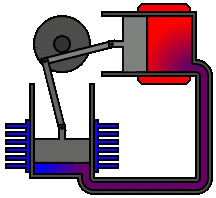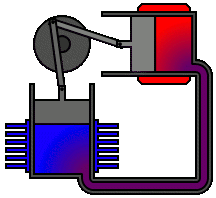
Re: This Week’s Finds in Mathematical Physics (Week 293)
You’ve an extra “x” in your URL.