This Week's Finds in Mathematical Physics (Week 290)

January 16, 2010

This Week’s Finds in Mathematical Physics (Week 290)

Posted by John Baez

$MathML-enabled post (click for more details).$

In week290 of This Week’s Finds, ponder the number of seconds in a week — and the number of inches in a mile. Read about categorification in analysis. Learn more about analogies between different kinds of physical systems, and meet the five most popular 1-ports: resistances, capacitances, inertances, effort sources and flow sources. And take stock of where we stand in our tour of rational homotopy theory!

$MathML-enabled post (click for more details).$

Also, guess what’s going on here:

Do you see trees?

Posted at January 16, 2010 2:14 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2155

36 Comments & 0 Trackbacks

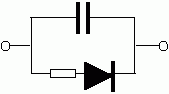
Re: This Week’s Finds in Mathematical Physics (Week 290)

“A careful study of where these numbers came from would lead us down some very tangled paths, just like the question why there are 63360 inches in a mile.”

Wasn’t Grothendieck said to be obsessed with this question at some point? (“What is the definition of a meter?”)

Posted by: harrison on January 16, 2010 4:17 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

You can read a little about Grothendieck’s meter question here. For example:

In his correspondence with Leila Schneps, he told her he would be willing to share his research into physics with her if she could answer one question: ‘What is a metre?’

Posted by: John Baez on January 16, 2010 4:55 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

The link led me to the short biography of Grothendieck, and that reminded me of a little anecdote I heard when I was an undergraduate in Goettingen: If you have visited the mathematical institute, you may have noticed that there are posters all over the walls, each with an image, a short biography and an introduction to the work of one of the famous mathematicians that spent their career there. One of them was Carl-Ludwig Siegel. He is still known in Goettingen for opposing the “cosmically general” viewpoint that Grothendieck and the Bourbaki group became famous for. He used to dismiss their kind of reasoning as “hom-hom-humming” .

Posted by: Tim vB on January 18, 2010 9:20 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

>until Jesse McKeown pointed me to a nice discussion of this issue here:

>>2) Bernard Brogliato, Rogelio Lozano, Bernhard Maschke and Olav Egeland, Dissipative Systems Analysis and Control: Theory and Applications, 2nd edition, Springer, Berlin, 2007.

er… when did I do that??? I think you meant someone else!

Posted by: Jesse McKeown on January 16, 2010 4:33 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Whoops! It was Tim vB.

Posted by: John Baez on January 16, 2010 4:38 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

As a general curiousity, the number of hours in a week is also the total number of pips on a set of dominoes (on a set where the highest is double 6, which is the overwhelmingly common type in Britain). I can’t see any bijection between those and either of the two groups of 168 elements yet (and the coincidence with hours in a week arise from there being (6*8)/2 hours in a day and 7 days in a week as the number of sum of “up to double- $n$ ” pips is $n(n+1)(n+2)/2$ .)

Posted by: bane on January 16, 2010 7:51 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Hocus pocus dominocus!

That ‘double pips number’ $n(n+1)(n+2)/2$ is thrice the tetrahedral number $n(n+1)(n+2)/6$ . So, 168 is also the number of balls in three tetrahedral stacks of cannonballs 6 high:

$3 \times (1 + 3 + 6 + 10 + 15 + 21) = 3 \times 56 = 168$

The only reason I noticed this was that I’m teaching a number theory course, and I led up to binomial coefficients by telling the kids about triangular numbers, tetrahedral numbers, pentatope numbers and so on. Maybe I can ask them to show that the total number of pips on a double-18 set of dominoes is the number of cannonballs in three tetrahedral stacks 18 high, namely 3420.

Posted by: John Baez on January 16, 2010 5:39 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

For example, suppose you want to balance a pole on your finger. How should you move your finger to keep the pole from falling over? That’s a control theory problem. You probably don’t need to read a book to solve this particular problem: we’re pretty good at learning to do tricks like this without thinking about math. But if you wanted to build a robot that could do this - or do just about anything - control theory might help.

I mentioned over here that an ex-colleague of mine, Carl Edward Rasmussen, was using machine learning techniques to solve this problem. He showed me footage of a real cart being moved along a track to support a rod. At first it gets it hopelessly wrong, but quickly it gets better via reinforcement learning.

He also showed me computer simulated version of learning to balance an articulated rod. Obviously it takes longer, but it still managed.

The ultimate challenge is to get a robot to ride a unicycle, something his control theory colleagues haven’t managed to do.

You can see some explanation and simulations of the single rod learning here. For the technical details of how Gaussian processes do the trick see this.

Posted by: David Corfield on January 16, 2010 10:06 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Very interesting footage!

One can imagine a circus with robot gymnasts doing tricks that require superhuman coordination — or tricks too dangerous for humans to risk. But if they can’t ride unicycles yet, much less do stuff like this, maybe the humans will stay in business for a little while.

Posted by: John Baez on January 16, 2010 5:13 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

One small difference is that when humans feel themselves falling to one side, they twist their upper body to turn the motion into a forward or backward fall, which is then controllable by pedal power. They use a flywheel for the robot.

But now I see that a Japanese team has managed to make one and a companion.

Posted by: David Corfield on January 16, 2010 5:41 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

You can use gizmos this to stick

I think you meant “gizmos like this”.

Posted by: Mike Stay on January 16, 2010 4:31 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Yes, a bungled last-minute edit. Fixed!

Posted by: John Baez on January 16, 2010 4:43 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

http://spectrum.ieee.org/semiconductors/design/the-mysterious-memristor

In 1971, a University of California, Berkeley, engineer predicted that there should be a fourth element: a memory resistor, or memristor. But no one knew how to build one. Now, 37 years later, electronics have finally gotten small enough to reveal the secrets of that fourth element. The memristor, Hewlett-Packard researchers revealed today in the journal Nature, had been hiding in plain sight all along–within the electrical characteristics of certain nanoscale devices. They think the new element could pave the way for applications both near- and far-term, from nonvolatile RAM to realistic neural networks.

The memristor’s story starts nearly four decades ago with a flash of insight by IEEE Fellow and nonlinear-circuit-theory pioneer Leon Chua. Examining the relationships between charge and flux in resistors, capacitors, and inductors in a 1971 paper, Chua postulated the existence of a fourth element called the memory resistor….

Posted by: Jonathan Vos Post on January 16, 2010 8:26 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

http://spectrum.ieee.org/semiconductors/design/the-mysterious-memristor

Working link:

The Mysterious Memristor

Posted by: Toby Bartels on January 17, 2010 12:19 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Thank you, Toby Bartels. I’d rushed off to a book signing in Burbank and failed to do an end-to-end test. Good article, though, and very innovative thinking. Is there a categorification of the Memristor in those analogous domains?

Posted by: Jonathan Vos Post on January 17, 2010 1:38 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Thanks, Jonathan and Toby. Just so people know, Jonathan had written:

[http://spectrum.ieee.org/semiconductors/design/the-mysterious-memristor]( The Mysterious Memristor)

and Toby fixed it to:

[The Mysterious Memristor](http://spectrum.ieee.org/semiconductors/design/the-mysterious-memristor)

If you choose ‘Markdown’, the latter link will work. If you choose ‘Markdown with itex to MathML’, you can also do math in TeX. For more info, go to TeXnical issues.

But anyway: what’s a memristor? It’s a 1-port where the voltage $V$ , current $I$ and charge $q$ are related by:

$V(t) = M(q(t)) I(t)$

In other words, it’s like a resistor whose resistance depends on the charge. The function $M$ is called the memristance, because it’s like a resistance that ‘remembers’ something about the past current — since $q(t)$ is the time integral of $I(t)$ .

In the language of general systems theory, which I’m explaining in This Week’s Finds, the equation defining this 1-port is

$\dot{p} = M(q) \dot{q}$

Question: does someone know an analogue in the realm of mechanics, or some other realm?

Another question: why did Leon Chua focus attention on this particular 1-port? There are, after all, zillions of options besides this and the 5 that I listed (resistance, capacitance, inductance = inertance, voltage source = effort source, and current source = flow source).

Posted by: John Baez on January 17, 2010 1:44 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

When I looked at the article it seemed to make sense. There are 4 ways to relate one of $p$ and $\dot p$ to one of $q$ and $\dot q$ . Week 290 covered

$\dot p = R \dot q$ – resistance
$\dot p = (1/C) q$ – capacitance
$p = L \dot q$ – inertance/inductance

So we need something like

$p = M q$ – memristance

The IEEE article has

$\d v = R \d i$ – resistance
$\d v = (1/C) \d q$ – capacitance
$\d \phi = L \d i$ – inertance/inductance
$\d \phi = M \d q$ – memristance

So the derivative of your $p$ is their $v$ and $p$ is $\phi$ ?

Anyway I don’t see where the zillions of other options come from.

Posted by: David Corfield on January 17, 2010 9:04 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

David wrote:

When I looked at the article it seemed to make sense. There are 4 ways to relate one of $p$ and $\dot p$ to one of $q$ and $\dot q$ . Week 290 covered

$\dot p = R \dot q$ – resistance

$\dot p = (1/C) q$ – capacitance

$p = L \dot q$ – inertance/inductance

So we need something like

$p = M q$ – memristance

Okay, that’s starting to make sense.

Here you seem to be focusing attention on linear 1-ports that only relate two of the variables $p, q, \dot p, \dot q$ .

Anyway I don’t see where the zillions of other options come from.

There are zillions of 1-ports; in general a 1-port can be defined by any equation of the form

$f(p,q,\dot p, \dot q, t) = 0$

For example, any real-life resistor is nonlinear, so it has

$\dot p = r(\dot q)$

for some function $r$ . We get the linear resistor as the idealization where this function is perfectly linear. It’s nice to assume our resistors are linear, and make sure our gadgets operate in a regime where this approximation is good. But nonlinearity is not always just a ‘defect’; nonlinear circuit elements like diodes are incredibly important.

The Wikipedia article defines a memristor to have

$\dot p = m(q) \dot q$

and this is just one of zillions of possibilities I can imagine, like $\dot q = f( \dot p) q$ . But you seem to be saying we should integrate both sides of the above equation:

$p = M(q)$

and then assume $M$ is a linear function, so

$p = M q$

for some constant $M$ .

Unfortunately, if this linear equation holds we can always differentiate it and get

$\dot p = M \dot q$

which is the equation for a resistor. So, a linear memristor is just a resistor! The Wikipedia article says:

The definition of the memristor is based solely on fundamental circuit variables, similarly to the resistor, capacitor, and inductor. Unlike those three elements, which are allowed in linear time-invariant or LTI system theory, memristors are nonlinear and may be described by any of a variety of time-varying functions of net charge. There is no such thing as a generic memristor. Instead, each device implements a particular function, wherein either the integral of voltage determines the integral of current, or vice versa. A linear time-invariant memristor is simply a conventional resistor.

Now I understand what this means!

The IEEE article has

$\d v = R \d i$ – resistance

$\d v = (1/C) \d q$ – capacitance

$\d \phi = L \d i$ – inertance/inductance

$\d \phi = M \d q$ – memristance

So the derivative of your $p$ is their $v$ and $p$ is $\phi$ ?

Yes, $v$ means voltage and that’s what general systems guys call ‘effort’, $\dot p$ — or ‘force’ in mechanics. $\phi$ means flux linkage and that’s the thing whose time derivative is voltage — so it’s what general systems guys call ‘momentum’, $p$ .

Flux linkage is not something most people have a feel for. You need to think about inductors to understand it.

I like the Wikipedia list of 4 nonlinear circuit elements — I think this clearly explains why people like to focus attention on 4 nonlinear 1-ports, and how memristors fit into this picture.

Thanks for getting me to understand this stuff!

Posted by: John Baez on January 17, 2010 6:06 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Memristors are in the news.

Posted by: David Corfield on September 2, 2010 8:32 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Cool!

“Memristor memory chips promise to run at least 10 times faster and use 10 times less power than an equivalent Flash memory chip,” said Stan Williams, the HP Fellow who first demonstrated the memristor…

But:

Steve Furber, professor of computer engineering at the University of Manchester, explained that the potential benefits lie in the fact that memristors are “much simpler in principle than transistors”.

“Because they are formed as a film between two wires, they don’t have to be implanted into the silicon surface - as do transistors, which form the storage locations in Flash - so they could be built in layers in 3D,” he told BBC News.

“Of course, the devil is in the detail, and I don’t think the manufacturing challenges have been fully exposed yet.”

Posted by: John Baez on September 3, 2010 2:05 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Chua has a different opinion on these analogies:

“Electronic theorists have been using the wrong pair of variables all these years–voltage and charge. The missing part of electronic theory was that the fundamental pair of variables is flux and charge,” said Chua. “The situation is analogous to what is called Aristotle’s Law of Motion, which was wrong, because he said that force must be proportional to velocity. That misled people for 2000 years until Newton came along and pointed out that Aristotle was using the wrong variables. Newton said that force is proportional to acceleration–the change in velocity. This is exactly the situation with electronic circuit theory today. All electronic textbooks have been teaching using the wrong variables–voltage and charge–explaining away inaccuracies as anomalies. What they should have been teaching is the relationship between changes in voltage, or flux, and charge.”

Posted by: John Baez on January 17, 2010 1:56 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Mechanical equivalences of the memristor… in hydraulics, could it be the one-way valve, like the ones working in you heart and blood vessels? It’s not behaving exactly similar to a diode, because you need some force from the flow over time to open or close it. So in a limited way/period of time, it remembers the past flow, forward and backward. Sorry, just guessing, I did not study it. By the way, how does a diode fit in you scheme? It is considered passive, no? Many thanks btw for your great articles, very inspirational!

Posted by: Marcus Verwiebe on January 17, 2010 3:23 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

I’m glad you’re enjoying This Week’s Finds!

I’m sadly ignorant when it comes to electronics, so I’ll just look at the Wikipedia entry on diodes. Yes, diodes are passive. And this entry mentions the Shockley ideal diode equation:

$I = I_0 (e^{k V} - 1)$

where $I_0$ and $k$ are constants. So, when this holds the current is an exponential function of voltage, but with a constant subtracted off so the current is zero when the voltage is zero. But this equation is oversimplified in various ways.

There’s a nice Wikipedia article on diode modelling, which describes various popular ways of simplifying the Shockley ideal diode equation even further — e.g., linearizing it.

A cute fact I saw here: problems involving diodes can force us to become acquainted with the Lambert $W$ function, which we get by solving

$z = W e^W$

for $W$ .

Posted by: John Baez on January 17, 2010 8:33 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Thanks for addressing the diode question! I guess I am still sadly ignorant of mathematics, even if I *can* enjoy your articles (and this unique, excellent blog in general) quite often. So, the diode shows non-linear, but also time-independent response/resistance, while time-dependence (or rather history-dependence) = memory is the point of the Memristor. Can you comment on the one-way valve not being like a diode, because it *is* time-dependent in its behaviour?

Posted by: Marcus Verwiebe on January 18, 2010 4:13 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

How about for a hydraulic memristor a pipe that clogs up depending on how much water has flowed through? Nice if a flow in the opposite direction unclogged it.

Posted by: David Corfield on January 19, 2010 11:26 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

David suggested:

How about for a hydraulic memristor a pipe that clogs up depending on how much water has flowed through?

That sounds like a muddy river!

Posted by: Tim Silverman on January 19, 2010 11:44 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Marcus,

A one-way valve and a diode are pretty good analogues. A diode also needs a minimum effort, it has about 0.6 volts accross it. (Check out the wikipedia article on diode)

It is a non-linear element. Circuits with non-linear elements can have more than one steady state solution. So a suspect you could build an effective memristor from a network of non-linear elements with some inductors and capacitors.

In a sense, a fuse is a memristor too.

I’ll try to think of a circuit with more than one solution.

Gerard

Posted by: Gerard Westendorp on January 20, 2010 8:21 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Gerard Westendorp said:

I’ll try to think of a circuit with more than one solution.

You can build logic gates out of op-amps, and, e.g. a memory element out of two NAND gates. (Or two NOT gates, but then you don’t have any way to flip the state.)

Posted by: Tim Silverman on January 20, 2010 12:18 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Here is one with just passive components:

That is, if you look at it as a 2 port, it forms a non-linear resistance, with some memory. But perhaps this is not really what the original idea of the memristor was.

A resistor does not store any energy.
A capacitor stores electrostatic energy.
An inductor stores magnetostatic energy.
(Remember, they are used for their dynamical properties, but they *store* static field energy.)
A linear memristor should give a linear relation between stored electrostatic energy and stored magnetostatic energy. This is a weird device. Think of its mechanical analogue: Do we know a device that implements a linear relationship between position and momentum?

Gerard

Posted by: Gerard Westendorp on January 20, 2010 11:23 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Typo:

In hydraulics, an effort source is a pump set up to maintain a specified flow.

You want ‘flow source’ here.

Posted by: Toby Bartels on January 17, 2010 8:52 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

I think that this is a bit of an understatement:

63360 = 2⁷ × 3² × 5 × 11

It's very unusual for the number 11 to show up in the British system of units.

Indeed, it's very unusual for it to show up in any system of units!

On the other hand, it's unusual for 5 to show up in specifically the British system of units (whereas it's quite common in the metric system). Of course, the explanation here is not that interesting: someone just used a factor 10 for once to define a new unit.

Posted by: Toby Bartels on January 17, 2010 8:57 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

$MathML-enabled post (click for more details).$

Actually, Don Davis pointed out that it’s not unusual for the number 11 to show up in the US system of units.

The number of inches in a mile is divisible by $11$ is because there are $33/2$ feet in a rod. For the explanation of that, see my webpage. This fact in turn causes the number of square feet in an acre to be divisible by $11^2$ . In fact, there are $66 \times 66 \times 10$ square feet in an acre!

But here’s the really weird thing Don Davis pointed out: there are $231 = 3 \times 7 \times 11$ cubic inches in a US liquid gallon.

Why is that? I don’t know. The British imperial gallon is different.

This 11-ness of the gallon then infects other units: for example, a US liquid ounce is

$3 \times 7 \times 11 / 2^7$

cubic inches!

Posted by: John Baez on January 17, 2010 9:38 PM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

John wrote:

But here’s the really weird thing Don Davis pointed out: there are 231=3× 7 × 11 cubic inches in a US liquid gallon.

Why is that? I don’t know. The British imperial gallon is different.

Don Davis to the rescue again:

the definition of the old british wine gallon was a cylinder 7” across & 6” deep. if we use 3 1/7 as pi, then the cylinder’s volume comes to 3 × 7 × 11 cu. in.

Of course this just pushes the question back: why the heck would people want a gallon to be a cylinder 7 inches across and 6 inches deep?

The Wikipedia article suggests that originally a gallon was defined to be 8 pounds of wine.

But a US liquid gallon of water weighs about 8.3 pounds, depending on the temperature. So, who knows?

Posted by: John Baez on January 18, 2010 12:31 AM | Permalink | Reply to this

Re: This Week’s Finds in Mathematical Physics (Week 290)

Very silly digression on units: There are 5 cubic centimeters in a teaspoon. There are 3 teaspoons in a tablespoon. There are two tablespoons in an ounce, and 8 ounces in a cup. There are 12 oz of liquid in a typical American can of soda. By my reckoning, that makes 360 milliliters in a can of soda. Yet the label says 354. It seems that we are being shorted a bit more than a teaspoon of soda on a regular basis — if we drink soda. Ah, the wonders of rounding.

Posted by: Scott Carter on January 19, 2010 8:09 PM | Permalink | Reply to this

memristors, memcapacitors and meminductors; Re: This Week’s Finds in Mathematical Physics (Week 290)

Yuriy V. Pershin, Massimiliano Di Ventra, Neuromorphic, Digital and Quantum Computation with Memory Circuit Elements

“… Memory effects are ubiquitous in nature and the class of memory circuit elements - which includes memristors, memcapacitors and meminductors - shows great potential to understand and simulate the associated fundamental physical processes. Here, we show that such elements can also be used in electronic schemes mimicking biologically-inspired computer architectures, performing digital logic and arithmetic operations, and can expand the capabilities of certain quantum computation schemes….”

Posted by: Jonathan Vos Post on October 1, 2010 2:32 AM | Permalink | Reply to this

frontiers of nonlinear circuit theory; Re: This Week’s Finds in Mathematical Physics (Week 290)

First order devices, hybrid memristors, and the frontiers of nonlinear circuit theory
Authors: Ricardo Riaza
Subjects: Dynamical Systems (math.DS); Mesoscale and Nanoscale Physics (cond-mat.mes-hall)

Several devices exhibiting memory effects have shown up in nonlinear circuit theory in recent years. Among others, these circuit elements include Chua’s memristors, as well as memcapacitors and meminductors. These and other related devices seem to be beyond the, say, classical scope of circuit theory, which is formulated in terms of resistors, capacitors, inductors, and voltage and current sources. We explore in this paper the potential extent of nonlinear circuit theory by classifying such mem-devices in terms of the variables involved in their constitutive relations and the notions of the differential- and the state-order of a device. Within this framework, the frontier of first order circuit theory is defined by so-called hybrid memristors, which are proposed here to accommodate a characteristic relating all four fundamental circuit variables. Devices with differential order two and mem-systems are discussed in less detail. We allow for fully nonlinear characteristics in all circuit elements, arriving at a rather exhaustive taxonomy of C^1-devices. Additionally, we extend the notion of a topologically degenerate configuration to circuits with memcapacitors, meminductors and all types of memristors, and characterize the differential-algebraic index of nodal models of such circuits.

Posted by: Jonathan Vos Post on October 4, 2010 1:30 AM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

January 16, 2010