Triangulations of the Sphere (Part 2)
Posted by John Baez
Thurston’s paper Shapes of polyhedra and triangulations of the sphere is really remarkable. I’m writing about it in my next column for the Notices of the American Mathematical Society. Here’s a draft — which is also a much more detailed version of an earlier blog post here.
If you have suggestions or corrections, please let me know: I can try to take them into account before this is due on November 5th. Just don’t ask me to make this longer: I have a strict limit.
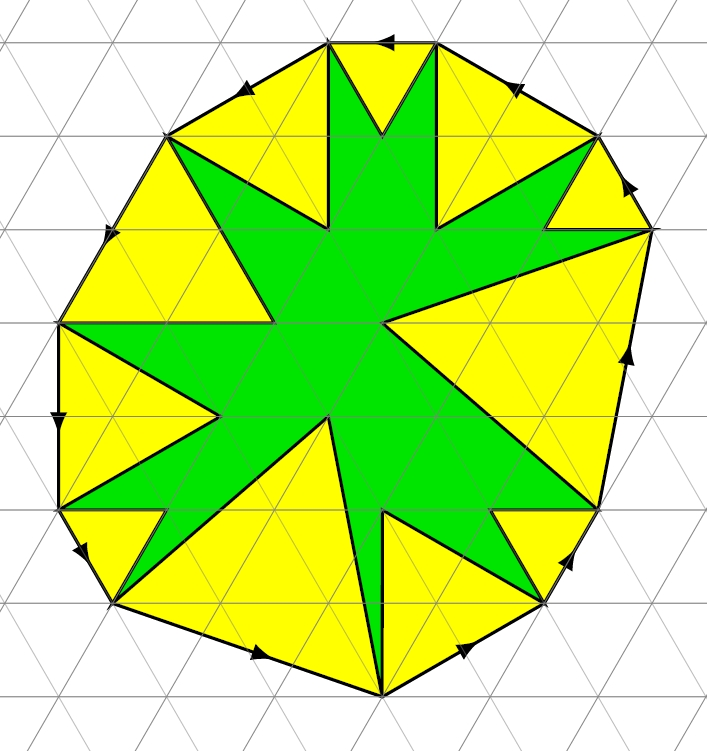
If you cut out this awkward-looking green star, you can fold it into a polyhedron where all 11 of the star’s tips meet at one point. This polyhedron is tiled by equilateral triangles, though some triangles get folded over. There are 12 points where 5 triangles meet: the 11 indentations in the star, and the point where all its tips meet. There are also some points where 6 triangles meet.
This may seem like a curiosity, but Bill Thurston discovered some profound facts about stars of this sort. Schwartz later wrote a useful account of Thurston’s work, and Engel and Smillie gave a very clear exposition of the algebraic aspects, while developing them further. I hope this brief introduction helps more people discover its charms.
To construct a star of this sort, first draw the lattice of Eisenstein integers in the complex plane:
where . Connecting nearest neighbors, you get the small gray equilateral triangles shown above. Then draw an 11-sided polygon whose vertices are Eisenstein integers. Along each edge of , draw a yellow equilateral triangle pointing inward. Make sure to choose the polygon so that these yellow triangles touch each other only at its corners.
If you remove these yellow triangles, you are left with an 11-pointed star, like the one shown in green above. Surprisingly, you can always fold up your star so all its tips meet at one point, forming a polyhedron tiled by equilateral triangles: the triangles coming from the lattice of Eisenstein integers. This polyhedron is homeomorphic to a sphere, so you have constructed a triangulation of the sphere for which 5 or 6 triangles meet at each vertex. And Thurston proved a remarkable fact: you can get all such triangulations using this method!
”A triangulation of the sphere where 5 or 6 triangles meet at each vertex” is a purely topological, or combinatorial, concept. But Thurston noticed that whenever you have such a thing, you can make all its triangles into flat equilateral triangles with the same edge length. This gives the sphere a geometry. To be precise, this gives it a flat Riemannian metric except at the points where 5 triangles meet at a vertex.
Your triangulation thus gives the sphere a flat Riemannian metric, except at finitely many points. The total angle around each of these points is not , only , because only 5 equilateral triangles meet there. These points are called ‘cone points’, and we say they have an ‘angle deficit’ of . By a discrete version of the Gauss–Bonnet theorem the total angle deficit must be , so there must be 12 such cone points.
Thurston showed that up to rescaling, any Riemannian metric on the 2-sphere that is flat except at 12 cone points with angle deficit arises from this procedure. The most famous example is the regular icosahedron, where 5 equilateral triangles meet at each vertex. Can you see how to draw an 11-sided polygon that gives the regular icosahedron? If you give up, you can see at the bottom of this page how Gerard Westendorp did it.
For deeper results, you can encode your polygon as a 10-tuple of Eisenstein integers. If you start at any corner of and walk all the way around its edges, you get 11 vectors shown as arrows in the figure. This gives an 11-tuple of Eisenstein integers . Since a round trip gets you back where you started, these Eisenstein integers sum to zero. Thus, is determined up to translation by a point .
Since areas depend quadratically on lengths, it is not surprising there is a real-valued quadratic form on such that the number of triangles in the triangulation equals . By a general result in linear algebra, there is a unique hermitian form on such that . Engel and Smillie give a nice explicit formula for this hermitian form in Section 3 of their paper. It has signature , meaning that we can find some complex coordinates on such that
This is reminiscent of 10-dimensional Minkowski spacetime, beloved by string theorists: that is, with the quadratic form
where the first dimension represents time and the rest describe space. Is this is a coincidence? I do not know.
Thurston studied the so-called ‘moduli space’ of all ways of giving a sphere a flat Riemannian metric with 12 cone points having nonnegative angle deficits. By definition, any such metric gives a point in , and two such metrics give the same point if and only if they are isometric. He showed is open and dense in the space , where
and is a certain discrete group of linear transformations of preserving both and the lattice .
Thurston also studied this larger space , and showed it is the moduli space of flat Riemannian metrics on the sphere with at most cone points and nonnegative angle deficits. So, elements of correspond to metrics with 12 distinct cone points, but when two or more cone points collide we get an element of . is a complex manifold, but is a more singular space, called an ‘orbifold’. By Alexandrov’s uniqueness theorem, any element of can be realized as a convex polyhedron, unique up to congruence.
Finally, sitting inside we have the discrete set . Points in here correspond to triangulations of the sphere where no more than 6 triangles meet at a vertex. For example, the regular octahedron and regular tetrahedron each give a point in this set.
Acknowledgements
I thank Leo Stein for showing me how to draw the figure and improving my exposition. Here is Gerard Westendorp’s polygon that gives the icosahedron. Note that after you fold up the star, 5 small equilateral triangles meet at each vertex:


Re: Triangulations of the Sphere (Part 2)
Heribert Schütz wrote a program that lets you take various 11-pointed stars of the sort described above and fold them up:
https://hcschuetz.github.io/polyhedron-star/dist/
Gerard Westendorp then used this program to create an animation of such a star being folded up!