The n-Category Café

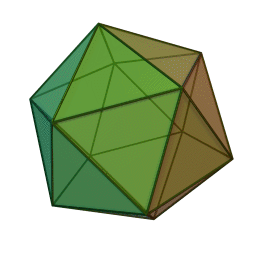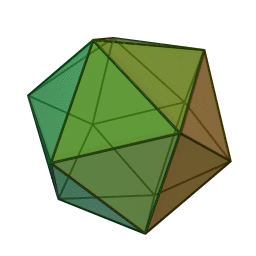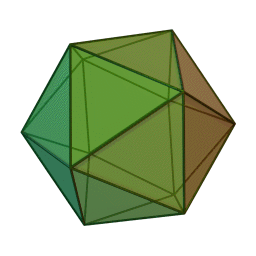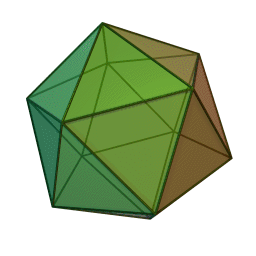
If you cut out the yellow shape here, you can fold it up along the red lines, and all 11 sharp tips will meet at one point! You’ll get a polyhedron with 12 corners, tiled by equilateral triangles. 5 triangles meet at each corner. There are also places where 6 triangles meet: these places are flat. Some triangles get folded along the red lines.

This may seem like a curiosity. But it shows up in a paper by the great mathematician Bill Thurston, and there’s a lot more to it.

Here’s how he drew this picture. First he drew a lattice of equilateral triangles on the plane. Then he drew an 11-sided polygon whose corners are lattice points. Along each edge of this polygon, he drew a green equilateral triangle pointing inward. If you cut out these green triangles, you’re left with the yellow shape, which you can fold up.

There are lots of ways you can draw such an 11-sided polygon; the picture shows just one. Each way gives a way of triangulating the sphere where the number of triangles meeting at a vertex is always either 5 or 6. In fact—and this is not obvious—you can get all such triangulations using this trick.

Maybe you can figure out how to get this one, the most symmetrical of all:

Is anyone out there willing to draw such an 11-sided polygon and then draw the polyhedron you get when you cut out the green triangles and fold up the left-over yellow shape? A super-genius could write a program where the user could choose any 11 points that define a valid polygon, and then the program would show what happens when you fold up the yellow shape. But I’d be thrilled to see just one example.

“A triangulation of the sphere where 5 or 6 triangles meet at each vertex” is really just a topological, or combinatorial, concept. But Thurston noticed that whenever you have such a thing, you can make all the triangles be flat equilateral triangles. Then you’ve given the sphere a geometry! To precise, you’ve given it a flat Riemannian metric except at the points where 5 triangles meet at a vertex. There need to be 12 of those points, by Euler’s formula V - E + F = 2.

So, you get a sphere with a flat Riemannian metric except at 12 points. The total angle around these points is not 360°, only 300°, because only 5 equilateral triangles meet there. These points are called ‘conical singularities’, and we say they have an ‘angle deficit’ of 60°.

Thurston showed you can get any such sphere by drawing an 11-sided convex polygon in a lattice of equilateral triangles and following the procedure above. (You have to make sure the green triangles don’t overlap.)

He even studied the so-called ‘moduli space’ of all ways of giving a sphere a flat Riemannian metric with 12 conical singularities with nonnegative angle deficits. He showed the compactification of this moduli space is the quotient of a 9-dimensional complex manifold, namely complex hyperbolic 9-space, by a discrete group action! And he studied how this moduli space contains the specially nice cases I’ve been discussing, where all the angle deficits are 60°.

Besides Thurston’s paper, I recommend these others:

• P. Engel and P. Smillie, The number of convex tilings of the sphere by triangles, squares, or hexagons.

• R. E. Schwartz, Notes on shapes of polyhedra.

This math here is incredible. But it took me a while to understand it, so I’m writing a column for the AMS Notices which may ease the way for future readers.