Classification of Metric Fibrations
Posted by Tom Leinster
Guest post by Yasuhiko Asao
In this blog post, I would like to introduce my recent work on metric fibrations following the preprints Magnitude and magnitude homology of filtered set enriched categories and Classification of metric fibrations.
Introduction
First, we introduce the place we work, , that is a category of categories enriched over the category of filtered sets (). The symmetric monoidal category contains and as full submonoidal categories, hence the category contains and (category of generalized metric space). Then by the framework of Leinster and Leinster–Shulman, we can consider the magnitude of “finite” -categories, that is an extension of both of the Euler characteristic of finite categories and the magnitude of finite metric spaces, introduced by Leinster.
Second, we give a description of metric fibration, introduced by Leinster, as the “Grothendieck fibration”. In precise terms, we generalize the notion of Grothendieck fibration of small categories in -enriched setting, and then we restrict it to (category of metric spaces). Such a restriction coincides with the definition of metric fibrations. Further we obtain the notion of metric actions that plays a role of lax functors in case, and we show a correspondence between them via the Grothendieck construction.
Finally, we give a classification of metric fibrations, which is parallel to that of topological fiber bundles. That is, the classification of metric fibrations is reduced to that of “principal fibrations” (torsors in ), which is done by the “1-Čech cohomology” in an appropriate sense. Further, we can define the “fundamental group ” of a metric space , which is a group object in , such that the conjugation classes of homomorphisms corresponds to the isomorphism classes of -torsors over . Namely, it is classified like topological covering spaces.
Filtered sets
First of all, we introduce a workspace that contains and . This large category inspires us to deal with objects sometimes like a small category and sometimes like a metric space.
Definitions
A filtered set is a set with subsets for any satisfying that for any and . We formally define that for .
A filtered map } is a map with for any .
We define by .
For , we define if . We have for any .
We denote the category of filtered sets by . We can consider as the subcategory of separated presheaves in , and then the tensor product is the Day convolution.
We denote the yoneda functor by . The filtered set consists of only one element with degree . Note that . It can be checked that is a symmetric monoidal category with the unit object .
Further, there is a symmetric monoidal embedding sending a set to a filtered set with for any . Now we have the following left diagram of monoidal embedding, that induces the right diagram of embedding.

Here, we denote the category of -categories by . We also denote the category of -categories by , the category of generalized metric spaces.
Benefits from
Examples of magnitude
Before we consider metric fibrations from our view point , we list up here some other benefits we obtain from there.
We can define magnitude and (co)weighting on a class of -categories with a finiteness condition. It contains usual magnitude and (co)weighting of finite metric spaces, and also the Euler characteristic of finite categories introduced by Leinster.
We can consider magnitude (co)weighting for broader class of metric spaces than so far. (This is actually not a benefit from the consideration of essentially, but I reached it in the process of defining magnitude on . ) Namely, we can consider magnitude (co)weighting of locally finite graphs being not necessarily finite.
If a metric space is finite, then we can compute its magnitude by summing up the magnitude (co)weighting. If a graph is not finite, it is not possible since the sum diverges, however, we can still consider its (co)weighting when the graph is locally finite.
For example, let’s consider the Cayley graph of a finitely generated group. Then its magnitude (co)weighting takes the same value at each vertex, and it coincides with the inverse of growth series. The growth series of a finitely generated group is defined as . Here, is the word length with respect to a generating system, and the “inverse” is taken in the formal power series ring . This observation may be a foothold for applying magnitude theory to geometric group theory. We can also consider the Poincaré polynomial of a ranked poset as a magnitude weighting. (This is possible without extending the definitions of magnitude.)
MH as HH
We can also define magnitude homology of -categories. Leinster–Shulman pointed out that the magnitude homology has a form of Hochschild homology in a generalized sense. Here, by considering a metric space like a small category in , we obtain a more ring theoretic description.
Theorem For , we have an isomorphism for any . Hence we have
Here, is the “category algebra of -categories” defined as follows.
Definition For , we define a filtered ring by:
with as a filtered abelian group.
For any , we define an associative product by
We also define an action of on the abelian group from the right and the left by
and
We use techniques of homology theory for small categories to give such an expression. This can also be considered as a kind of generalization of Gerstenhaber–Schack’s theorem asserting that the cohomology of a simplicial complex is isomorphic to the Hochschild homology of the incidence algebra.
Homotopies on
By the usual nerve construction for small categories, we can construct a filtered simplicial set and filtered chain complex from a -category. We say a filtered set is -filtered if any has an integral degree. We denote the category of -filtered sets by .
For a -category, we have a -filtered chain complex by the above construction, and we can construct a spectral sequence from it. Then we have the following.
Theorem Let .
.
If is a digraph, we have , where denotes the reduced path homology introduced by Grigor’yan–Muranov–Lin–S.-T. Yau et al.
It converges to the homology of the underlying small category if it converges, in particular when is finite.
Now we discuss homotopy invariance of each page of this spectral sequence. We show that the -th page of this spectral sequence is invariant under “-homotopy”.
Two morphisms are -step -homotopic if there is a morphism with . Here, is the -category with just two objects and one non-trivial morphism from to with degree .
The equivalence relation generated by “-steps” is the -homotopy. For example:
-homotopy for small categories is exactly the natural transformation.
-homotopy for digraphs is exactly the digraph homotopy.
-homotopy for metric spaces is exactly the -closeness of Lipschitz maps. Namely, Lipschitz maps are -homotopic if and only if for any .
Theorem The -page of the above spectral sequence is invariant under -homotopy.
This contains the “digraph homotopy invariance of GLMY homology”. Further, this result suggests us that there are “-homotopy theories” on that are the lifts of the following model structures on filtered chain complexes.
Theorem (J. Cirici, D. -E. Santander, M. Livernet and S. Whitehouse) On the category of bounded filtered chain complexes, there is a model structure for each such that the weak equivalences are the chain maps inducing quasi-isomorphisms on the term.
We can also expect that the following cofibration category structure on digraphs is a part of the “1-homotopy theory”.
Theorem (D. Carranza, B. Doherty, M. Opie, M. Sarazola and L.-Z. Wong) On the category of digraphs, there is a cofibration category structure such that the weak equivalences are the digraph maps inducing isomorphisms on the GLMY homology.
Metric fibrations
Original definition by Leinster
First we recall the definition of metric fibration given by Leinster.
Definition (Leinster) Let be a Lipschitz map between metric spaces. We say that is a metric fibration over if it satisfies the following: for any and , there uniquely exists such that
,
for any .
We denote the category of metric fibrations over by . The morphisms are base and fiber preserving Lipschitz maps.
A remarkable property of the metric fibration is that the magnitude behaves like the Euler characteristic of topological fiber bundles as follows.
Proposition (Leinster) Let be a metric fibration. If is a finite metric space, then its magnitude is a product of those of and for any .
We note that fibers of are isometric.
Examples
For a product of metric spaces , the projection is a metric fibration.
The projection from the complete bipartite graph to is a metric fibration. Hence the magnitude of is same as that of as pointed out by Leinster.
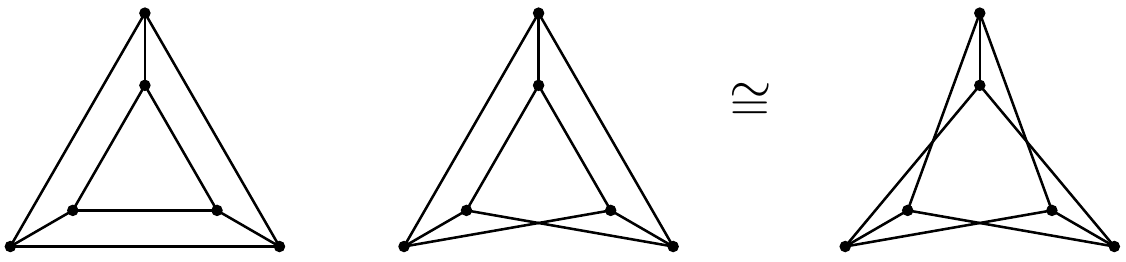
The graph on the left is , and the graph on the right is isomorphic to . They both have the magnitude .
Metric fibrations as Grothendieck fibrations
As is well known to category theorists, there is a notion of fibrations for small categories called Grothendieck fibrations, of which we don’t explain the definition here. This notion is equivalent to lax functors via the so-called Grothendieck construction, and we can generalize this story in -enriched setting. What is remarkable is that the restriction of such a generalized Grothendieck fibration to (the category of metric spaces and Lipschitz maps) is exactly the metric fibration. We define the metric counterpart of lax functors as follows.
Definition Let be a metric space.
A metric action consists of metric spaces for any and isometries for any satisfying the following for any :
- and ,
- for any .
A metric transformation consists of Lipschitz maps for any satisfying that for any . We can define the composite of metric transformations and by . We denote the category of metric actions and metric transformations by .
The equivalence of Grothendieck fibrations and lax functors is generalized to -enriched situation and restricted to as follows.
Theorem The Grothendieck construction gives a category equivalence
Classification of metric fibrations
Now we give a complete classification of metric fibrations by several means, which is parallel to that of topological fiber bundles. Namely, we define “principal fibrations”, “fundamental groups” and a “-Čech cohomology” for metric spaces, and obtain equivalences between categories of these objects. Roughly speaking, we obtain an analogy of the following correspondence in the case of topological fiber bundles with a discrete structure group.
Fiber bundles over with structure group
Principal -bundles over (-torsors)
We explain these correspondences in the following, and we start from the definition of torsors in .
-torsors
We can define a subcategory of that consists of “principal -fibrations” called -torsors. Here and in the following, a group is not just a group but is a group object of , which we call a metric group. Namely, it is a metric space as well as a group whose operations are all Lipschitz maps.
Definition Let be a group (not a metric one). A metric fibration is a -torsor over if it satisfies the following:
acts isometrically on from the right, and preserves each fiber of .
Each fiber of is a right -torsor in the following sense. Let be a group and be a metric space. We say that is a right -torsor if acts on from the right and satisfies the following :
- It is free and transitive.
- is an isometry for any .
- We have for any and .
For a -torsor , we can equip with a metric group structure that is isometric to any fiber of . Hence, in the following, we write “-torsors” instead of “-torsors”, where is such a metric group obtained from .
A -morphism between -torsors is a -equivariant map that is also a morphism of metric fibrations. We denote the category of -torsors over and -morphisms by . Note that the category is a subgroupoid of .
On the other hand, we can also define a subcategory of that is the counterpart of .
Definition Let be a metric space and be a metric group.
A -metric action is a metric action satisfying the following:
- for any .
- is a left multiplication by some for any .
Let be -metric actions. A -metric transformation is a metric transformation such that each component is a left multiplication by an element . We denote the category of -metric actions and -metric transformations by .
Apparently, is a subcategory of and is also a groupoid. Then we have the following.
Theorem The Grothendieck construction gives a category equivalence
Fundamental metric group
As an example of a metric group, we construct the fundamental metric group of a metric space . Roughly speaking, it is a collection of “loops in ” based at some , which are identified by a “homotopy relation”. In precise terms, we define it as follows.
Definition Let be a metric space and .
For each , we define a set by We also define that .
We define a connected graph with the vertex set as follows. For , an unordered pair spans an edge if and only if it satisfies both of the following :
- There is an such that and .
- There is a such that for and for , where we have and .
We equip the graph with a weighted graph structure by defining a function on edges by
where we use the notation as in the previous bullet point.We denote the quasi-metric space obtained from the weighted graph by . Let be the metric space obtained from by identifying points with distance . The metric space has a metric group structure given by the concatenation. We call the metric group the fundamental metric group of with the base point .
We sometimes write since it does not depend on the choice of the base point, similarly to the topological case. We also define a category of homomorphisms , where a morphism between homomorphisms is a conjugation relation. Then we have the following.
Theorem We have a category equivalence
As an example, we classify -torsors over cycle graphs as follows. We note that the notion of a metric group is equivalent to that of a “normed group” as E. Roff stated in her thesis. For a metric group , we denote the corresponding norm of an element by .
Proposition Let be an -cycle graph. Then we have Hence we have that for any metric group , which implies that there is only a trivial metric fibration over and that there is at most one non-trivial metric fibration over .
Associated bundle construction and structure groups
Now, similarly to the topological case, we can define an “associated bundle construction” from a torsor and a metric space .
First we give another example of a metric group. For a metric space , let be the group of self-isometries on . We define a distance function on by
Then is a metric group if is bounded. Even if not, it is an extended metric group that admits as a distance. We suppose that is a metric group in the following, but the discussions can be applied to the extended case.
Now we can construct a metric fibration with fiber from a -torsor similarly to the topological case. This construction gives the following.
Theorem Suppose that is a bounded metric space. Then we have a category equivalence where is the full subcategory of that consists of metric fibrations with the fiber , and we denote the core of a category by .
Čech cohomology of -torsors
For a -torsor , we define a “-Čech cohomology” as a groupoid. This is an analogy from the Čech cohomology constructed from the local sections of a principal bundle. We first define the “local section” of a -torsor.
Definition Let be a -torsor. For , we define a local section of over a pair as a pair of points such that and is the lift of along .
We say that is a local section of if each is a local section of over a pair and satisfies that .
Now we would like to define a cocycle from the differences of any pair of adjacent local sections. Before that, we define the Čech cohomology in general.
Definition Let be a metric space and suppose that points of are indexed as . For a metric group , we define the -cohomology of with coefficients in as the category by and where we denote the conjugation-invariant norm on by . In the above, we used the notation for defined as We call an object of a cocycle. The category is in fact a groupoid.
Proposition Let be a -torsor. For a local section of , we can construct a cocycle . Further, for any two local sections of , the corresponding cocycles and are isomorphic.
Conversely we can construct a -torsor from a cocyle by pasting copies of ’s along the cocycle. Then we have the following from these correspondences.
Theorem We have a category equivalence

Re: Classification of Metric Fibrations
There are tons of ideas here! So I’m not sure where to start. But maybe I’ll start near the end, with the definition of the fundamental metric group of a metric space with basepoint .
You give as an example that the -cycle graph has fundamental metric group if is odd and the trivial group if is even. Can you give some more examples? E.g. what about taking to be some other graphs, such as trees? Or what about , or ?