Dividing a Square into Similar Rectangles
Posted by John Baez
If you divide a square into some fixed number of similar rectangles, what proportions can these rectangles have? We’ve been having fun thinking about this on Mathstodon, and here is a progress report.
If you divide a square into 3 similar rectangles, what proportions can these rectangles have? There are three options. The third is much more complicated than the first two:
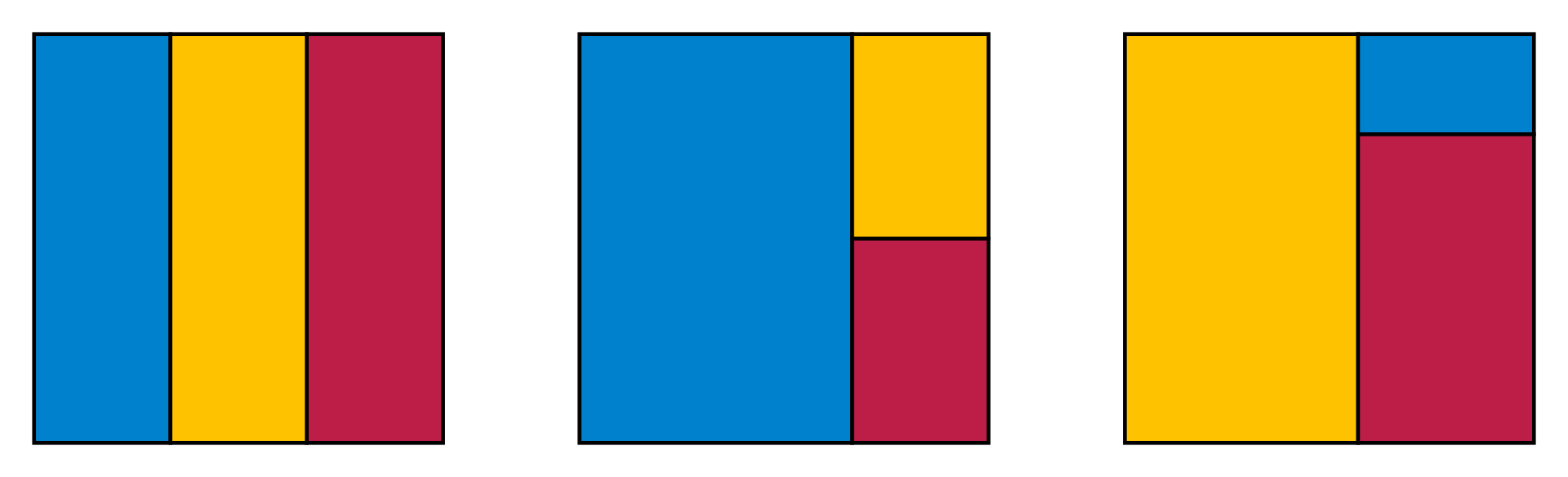
We can divide the square into three rectangles that are 1/3 as long in one direction as the other, as in the first picture.
We can divide it into three rectangles that are 2/3 as long in one direction as the other, as in the second picture.
We can divide it into three rectangles that are times as long in one direction as the other, as in the third picture.
What’s ? The yellow rectangle has height and width , so the blue rectangle has width and height , while the red one has width and height . The heights of the blue and red rectangles must sum to , so
or
and the solution of this cubic is
so
The reciprocal of this number is the square of a famous constant: the plastic ratio, . This is like a cheap imitation of the golden ratio, with
Why is the third option so much more complicated than the other two? As we’ll see, it’s because the first two have all the rectangles ‘pointing the same way’, while the third does not: it has a mix of rectangles ‘standing up’ and ‘lying down’.
To see the pattern, it helps to do a harder problem.
If you divide a square into 4 similar rectangles, what proportions can these rectangles have? A lot of people on Mathstodon worked on this puzzle! Here Dan Piker lists the 11 options we’ve found:

Note: there are more than 11 ways to divide a square into 4 similar rectangles, since you can rotate and reflect these pictures, and also rearrange the rectangles in some of them. But we’ve only found 11 possible proportions for the rectangles. Stefano Gogioso has sketched a proof that these are all the options, and Rahul Narain has given a computerized proof that these are all the options obtained from ‘guillotine cuts’:
- Wikipedia, Guillotine partition.
A ‘guillotine cut’ is a straight line going from one edge of an existing polygon to the opposite edge. And I believe there’s no way to dissect a square into 4 rectangles that doesn’t use guillotine cuts.
In the process of listing the options, we discovered something interesting: the rectangles have rational proportions only in options 1, 4, 7, 10 and 11 here:
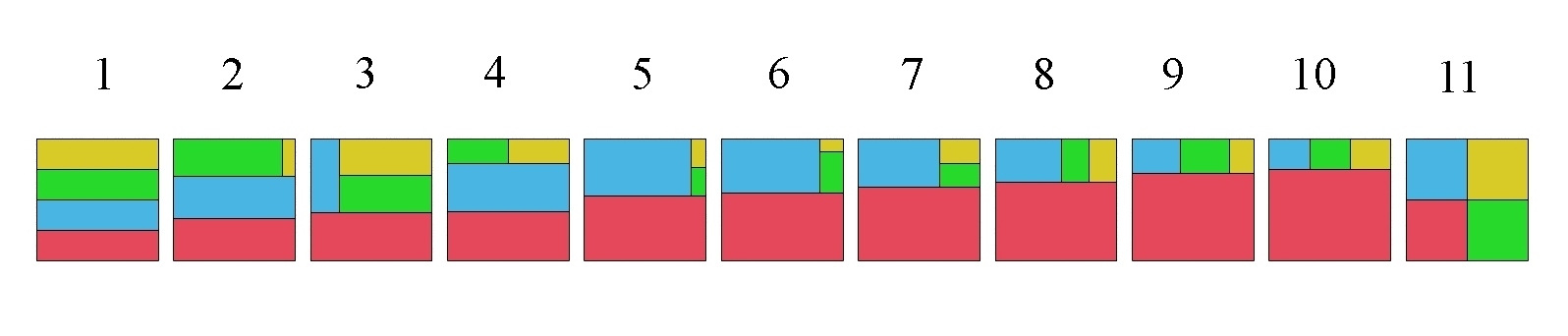
And these are precisely the options where all the rectangles are pointing the same way! (They happen to all be lying down, wider than they are tall. But of course they’d all be standing up if we rotated the pictures.)
Puzzle 1. Show that if you subdivide a square into similar rectangles that are all pointing the same way, the ratio of their short side to their long side must be a rational number.
Puzzle 2. Show that the converse is not true.
We also discovered another pattern, too: when is not rational, it is the solution to a cubic equation with integer coefficients.
Does this other pattern persist when we subdivide a square into 5 similar rectangles? No, alas! Ian Henderson and Rahul Narain seem to have shown that exactly 51 proportions are possible when we subdivide a square into 5 similar rectangles. Henderson drew them:

while Narain listed the polynomial equations obeyed by the 51 possible proportions. Some obey a quartic equation with integer coefficients, not a cubic.
To be honest, Narain only considered ways of subdividing a square into 5 similar rectangles using guillotine cuts. But this should be okay, since I believe there’s just one way to subdivide a square into 5 rectangles that cannot be done using guillotine cuts. It’s shown here in a paper by Robert Dawson, in fact:
However, when we try to make all 5 rectangles similar, the central one shrinks to a point.
Ian Henderson also believes that when you subdivide a square into 6 similar rectangles, 245 proportions of rectangles are possible:
And for subdivisions of a square into 7 similar rectangles, he believes 1371 proportions are possible:
You can click to enlarge these last two pictures.
However, he adds, “I’m not 100% confident in these numbers.” So, someone should check his work.
Puzzle 3. Show that you can divide a square into 6 similar rectangles in a way that cannot be done via guillotine cuts.
Okay, back to something simpler: what proportions are possible when we divide a square into 4 similar rectangles? Let’s work it out!
For each option we get a number describing the proportion of the rectangles that subdivide the square. This number is the length of the short side divided by the length of the long side. The 11 options below are listed from the smallest possible value of to the largest.

1) Option 1 is to divide the square into 4 rectangles that are 1/4 as tall as they are wide. So, the number we get from this option is 1/4.
Note that if we rotated this option we’d get tall skinny rectangles, but the number would still be 1/4.
2) In option 2, the bottom two rectangles have width 1 and height . Thus the top two have height .
Since the green rectangle is times as tall as it is wide, its width must be . The yellow rectangle thus has width
Its height is this divided by , namely . But we know its height is , so
or
so

3) For option 3 the red rectangle has height , so the blue one has height and width , so the other two have width = and height . The total height of red, green and yellow is so or
This gives
4) Option 4 is nice: it has left-right symmetry, and its rectangles can be rearranged to give another option with left-right symmetry.
The red and blue rectangles have height . The green and yellow ones thus have height , and thus width . But by symmetry we know they must have width 1/2, so
or
or
or
Not a cubic equation this time—linear! So x is rational.

Notice that options 3, 5, 6, and 7 are all topologically the same. They were analyzed by Lisanne, and her work helped me a lot.
5) In option 5 the red rectangle has height , so the blue has height and thus width . The yellow and green thus have width , hence height .
The heights of yellow, green and red must sum to 1:
so we get a cubic:
and the solution is
6) In option 6 the red rectangle again has height , so the blue again has height and width .
The yellow and green again have width , but now they’re different: the yellow has height while the blue has height .
The heights of yellow, green and red sum to :
so
or

7) In option 7, like options 5 and 6, the red rectangle has height , so the blue has height and width .
Thus, the yellow and green again have width . But this time both have height .
Yet again, the heights of yellow, green and red sum to 1:
so
and
The equation was linear, so is rational!
Options 8, 9, and 10 are also all topologically the same.
8) In option 8 the red rectangle has height so the blue has height and width . The green and yellow also have height , but width .
The widths of blue, green and yellow sum to 1:
so
and

9) In option 9 the red rectangle has height so the blue and green have height and width . The yellow also has height , but width .
The widths of blue, green and yellow sum to 1:
so
or
so
10) Option 10 is more symmetrical than 8 or 9 since all three rectangles on top are congruent.
The red rectangle has height so the blue, green and yellow all have height and thus width .
The widths of blue, green and yellow sum to 1:
so
or
or
Another linear equation, with a rational solution!

11) Finally, option 11 is the second one where all four rectangles are congruent. This time they’re squares! Clearly
So, we see in these examples that is rational precisely when all rectangles are ‘pointing the same way’: in the way Dan drew them, they’re all at least as wide as they are tall.
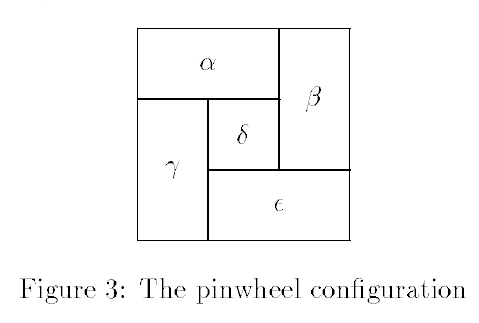
I’m not quite sure where to go with this research next. But I think the connection to double categories, hinted at in this paper with the picture of the pinwheel configuration, is interesting:
- Robert Dawson, A forbidden-suborder characterization of binarily-composable diagrams in double categories, Theory and Applications of Categories 1 (1995), 146–153.
Maybe we should seriously study the double category where 2-cells are rectangles that are subdivided into smaller rectangles by guillotine cuts!
But I also keep hoping there’s some interesting number-theoretic significance to the proportions that come up when we divide a square into the similar rectangles. Can anyone see interesting patterns in Rahul Narain’s table of the polynomials obeyed by these ratios when we divide a square into 5 similar rectangles? It might be easiest to start by focusing on the rational numbers. His is my :
u - 5 u^3 - 4*u^2 + u - 3 u^3 - 4*u^2 + 2*u - 4 2*u - 7 u^3 - 4*u^2 + 3*u - 3 2*u^3 - 6*u^2 + u - 2 u^3 - 3*u^2 + 2*u - 5 u^3 - 3*u^2 + 2*u - 4 2*u^3 - 6*u^2 + 2*u - 2 u^3 - 3*u^2 + u - 1 3*u - 8 u^3 - 3*u^2 + 3*u - 5 2*u^3 - 5*u^2 + u - 2 u^5 - 3*u^4 + 3*u^3 - 4*u^2 + u - 1 -2*u^2 + 6*u - 3 2*u^3 - 5*u^2 + 2*u - 3 3*u - 7 u^4 - 3*u^3 + 3*u^2 - 4*u + 2 2*u^3 - 5*u^2 + 3*u - 3 u^3 - 3*u^2 + 4*u - 4 -u^2 + 4*u - 4 4*u - 8 3*u^3 - 6*u^2 + u - 1 2*u^3 - 4*u^2 + 2*u - 3 u^3 - 2*u^2 + 3*u - 5 3*u^3 - 6*u^2 + 2*u - 2 u^5 - 2*u^4 + 3*u^3 - 5*u^2 + u - 1 2*u^3 - 4*u^2 + 3*u - 4 4*u - 7 u^3 - 2*u^2 + 4*u - 6 -u^3 + 3*u^2 - 4*u + 3 2*u^3 - 5*u^2 + 4*u - 2 2*u^3 - 4*u^2 + 3*u - 3 3*u^3 - 5*u^2 + 2*u - 3 5*u - 8 u^5 - 2*u^4 + 3*u^3 - 4*u^2 + u - 1 -3*u^2 + 6*u - 2 2*u^4 - 4*u^3 + 3*u^2 - 3*u + 1 3*u^3 - 5*u^2 + 2*u - 2 4*u^3 - 6*u^2 + u - 1 -2*u^3 + 4*u^2 - 3*u + 2 2*u^3 - 3*u^2 + 3*u - 4 u^5 - 2*u^4 + 3*u^3 - 4*u^2 + 2*u - 1 5*u - 7 u^3 - 2*u^2 + 3*u - 3 2*u^3 - 3*u^2 + 2*u - 2 -u^3 + 2*u^2 - 4*u + 4 3*u^3 - 5*u^2 + 3*u - 2 3*u^3 - 4*u^2 + u - 1 4*u^3 - 6*u^2 + 2*u - 1 4*u - 5 2*u^3 - 3*u^2 + 4*u - 4 -5*u + 6 6*u - 7



GARTH
What if instead of a square, you require the outer rectangle to have the same aspect ratio as the pieces?
The results for 2 and 3 pieces have similar arrangements to the square ones (I suspect this will generally be the case), but of course the numbers are different: sqrt(2)/2, sqrt(3)/3, (-1+sqrt(17))/4, and a cubic root approximately equal to 0.72449.
The first rational number (1/2) doesn’t show up until 4 pieces.