The n-Category Café

This blog post is a continuation of the third entry in this series of blog posts. You might want to have a look at if first for some further motivation on the questions to come. We continue the numbering of problems from our third blog post.

Some geometric problems

At the heart of the Leinster-Willerton conjecture lies the statement that the magnitude function captures much of the geometry of a metric space. One might ask: how much?

From our geometric formulas for the first three expansion coefficients $c_j(X)$, it turns out that the first two appear in the Weyl law and all three appear in the heat trace expansion. Both describe the asymptotic behavior of eigenvalues of the Laplace operator in $X$ (with Dirichlet boundary conditions). Marc Kac’s famously asked “can you hear the shape of a drum”, or if a Riemannian manifold with boundary is determined up to isometry by the spectrum of its Dirichlet Laplacian. The spectrum of the Dirichlet Laplacian of a drum would be the frequencies heard when playing said drum, thus motivating the formulation.

We may paraphrase Kac’s question for magnitudes: “can you magnitude the shape of a drum”?

Kac’s question was answered negatively for closed manifolds by Milnor, who gave examples of two non-isometric 4-dimensional tori with the same spectrum of the associated Laplacians. For domains in Euclidean space, Gordon, Webb and Wolpert gave an example of two non-isometric polygonal domains in the plane with the same spectrum of the associated Dirichlet Laplacian. We note that the case of domains with smooth boundary is open, in all dimensions. Returning to magnitudes, we formulate our problem.

Problem D. Are there two non-isometric domains in odd-dimensional Euclidean space with the same magnitude function? Are there infinitely many? What about the case for closed manifolds?

A simple example for non-isometric four-point metric spaces with the same magnitude function may be found in Example 2.3.5 of this paper by Leinster.

A second intriguing problem is to compute the geometric meaning of all expansion coefficients $c_j(X)$ in the expansion $\mathcal{M}_X(R)\sim \sum_{j=0}^\infty c_j(X)R^{n-j}$, when $X$ is a smooth domain. The results in our paper give a recipe and some structural results about $c_j(X)$. For $j=0,1,2$ we compute it and recent computations have been done for $j=3$ (the result is announced in our third blog post). At first we wanted to pose the computation of $c_j(X)$ as a problem, but already computing $c_{4}(X)$ by brute force looks like a complicated task that we would not give even to the worst of our enemies. So we refrained. New ideas seem to be needed. One idea from geometric analysis is that complicated invariants sometimes have simple variational formulas. For instance, analytic torsion is a complicated spectral invariant which is hard to compute even in examples, but variations in the input data can be computed by local expressions through the so called anomaly formula due to Brüning-Ma.

Problem E. Let $B$ denote the unit ball and $X$ a domain with smooth boundary. Compute the values of

$$c_{j,k}(X):=\frac{\mathrm{d}^k}{\mathrm{d}\epsilon^k}\bigg|_{\epsilon=0} c_j(X+\epsilon B).$$

Here $+$ denotes the Minkowski sum.

Compare this to Weyl’s tube formula, which gives a variational formula for the volume in terms of intrinsic volumes. Using that $c_0(X)=\mathrm{vol}(X)$, it follows that $c_{0,k}(X)=V_k(X)$ (the intrinsic volumes) if $X$ is convex. More generaly, for $j=0,1,2$, the invariants $c_{j,k}$ can be computed in terms of mixed volumes.

In the special case of a ball, Problem E relates to an observation by Simon Willerton, Conjecture 17 of his preprint.

Some analytic problems

The magnitude function extends meromorphically to $\mathbb{C}$ for compact metric spaces of a geometric origin, such as compact domains in $\mathbb{R}^n$ ($n$ odd) or closed Riemannian manifolds. The pole structure of the magnitude function for odd-dimensional balls is intriguingly regular, as is seen in the plots of poles for the magnitudes of the $n$-dimensional ball here, for $n=13,17,21$.

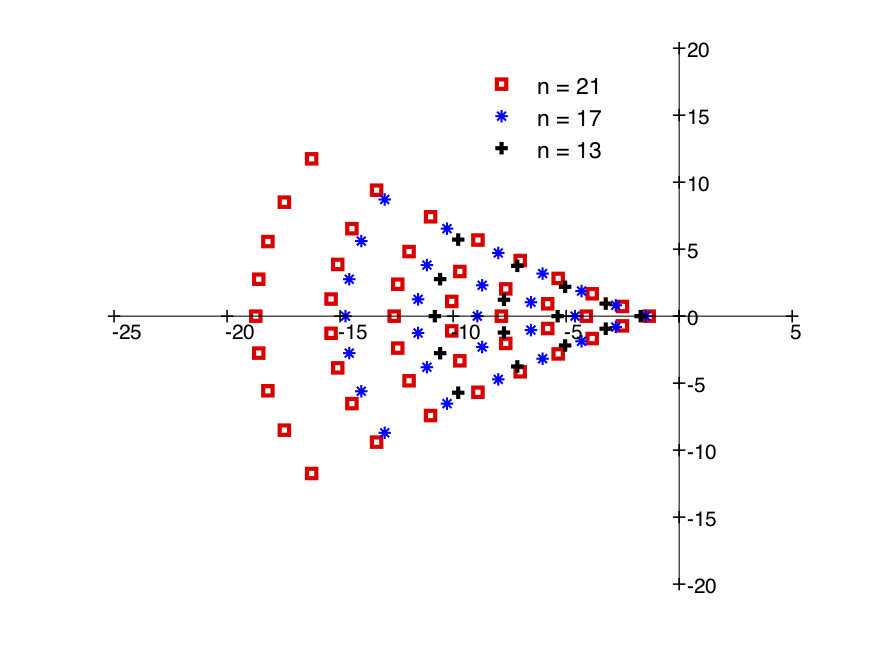
The picture for the zeroes of the magnitude of these odd-dimensional balls is similar.

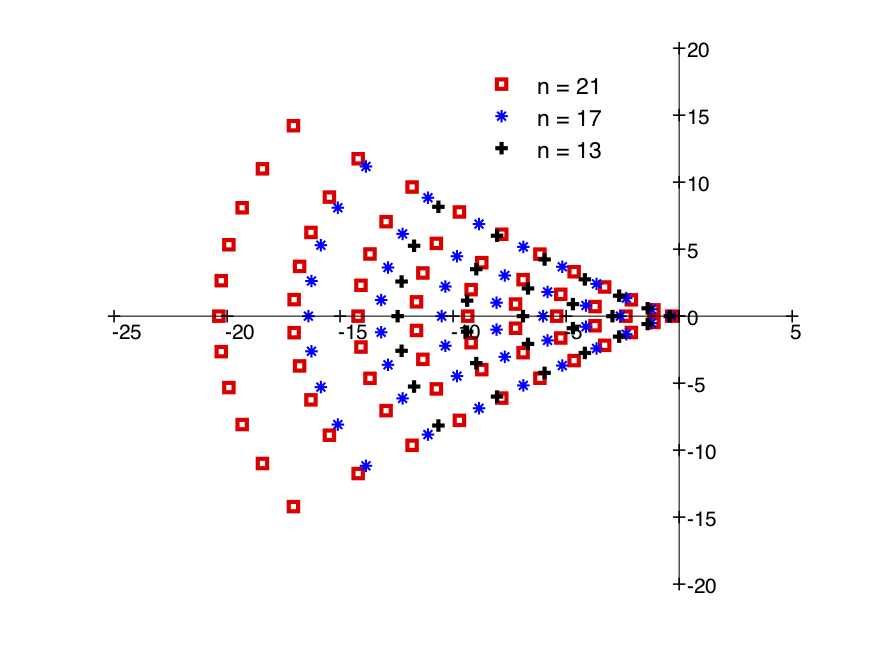
Computations of Willerton show that the magnitude function of such an $n$-dimensional ball is rational, with at most $\frac{n^2-3n+3}{8}$ poles which are empirically observed to lie in the sector $\{R \in \mathbb{C} : |\mathrm{arg}(R)|\geq \frac{3\pi}{4}\}$. Is there a deeper explanation? What is the role of the poles? For instance, why is $R=-3$ a pole for the magnitude function of the $5$-ball?

Quite little is known in the case of closed Riemannian manifolds. It is currently not even clear if there could be poles on the positive half-axis $R\gt 0$. The example of $S^2$ computed by Willerton (and discussed in our third blog post) shows that $\mathcal{M}_{S^2}(R)=\frac{2R+2}{1-\mathrm{e}^{-\pi R}}$ so the set of poles of magnitude of $S^2$ is $2i\mathbb{Z}$ (all simple poles).

Problem F. Is there a closed manifold with finitely many poles of magnitude?

More is known in the case of compact domains (with smooth boundary) in $\mathbb{R}^n$, $n$ odd. The poles are situated outside the sector where $|\mathrm{arg}(R)|\leq \pi/(n+1)$, and for any $C\gt 0$ there are finitely many poles in the sector $\mathrm{Re}(R)\gt C |\mathrm{Im}(R)|$. In scattering theory, convex domains have scattering poles that are contained even further into the left half-plane (even as far as to the left of some curve $|\mathrm{Im}(R)|^3=|\mathrm{Re}(R)|+C$ in the half-plane $\mathrm{Re}(R)\lt 0$ by results in the PhD thesis of Long Jin). This suggests that the convex situation is better behaved.

Problem G. What can be said about the number and location of poles of the magnitude function for a convex domain? Is the number of poles finite?

An interesting answer to this problem could be an example of a convex domain with infinitely many poles of magnitude.

Let us end this blog post by mentioning a formula that holds for spheres and flat two-dimensional torii. We have no reason to believe that it holds nor fails in general, but it is simply too beautiful to not mention. If $X$ is a sphere in its round metric or a flat two-dimensional torus, it holds that

$$\chi(X)=\mathrm{Res}_{R=0} \mathcal{M}_X(R).$$

For spheres, this formula follows from Willerton’s computations for the magnitude function of spheres and for torii it follows from a short computation. In geometric analysis, residues of zeta functions (and eta functions) play an important role. They can for instance be used to equate global invariants (like a Fredholm index) to a local invariant, and it would be most delightful if the above equation was not just a funny coincidence. Seeing that the asymptotics of the magnitude might not capture the Euler characteristic (as seen in dimension $3$ from the computation of $c_3$ mentioned in our third blog post), it would be interesting if the Euler characteristics could be found in the pole structure of the magnitude function instead.