The n-Category Café

Basic Machinery

Presently, our base of enrichment is the cartesian monoidal closed category $\mathbf{Cat}$ of (small) categories, with the usual adjunction $-\times\mathcal{A}\dashv[\mathcal{A},-]$. The very definition of an indexed limit requires a good command of the basic $\mathbf{Cat}$-categorical notions, as seen for example in “Review of the Elements of 2-categories” by Kelly and Street. In particular, a 2-natural transformation $\alpha:G\Rightarrow H$ between 2-functors consists of components which not only satisfy the usual naturality condition, but also the 2-naturality one expressing compatibility with 2-cells. Moreover, a modification between 2-natural transformations $m:\alpha\Rrightarrow\beta$ has components families of 2-cells $m_A:\alpha_A\Rightarrow\beta_A:GA\to HA$ compatible with the mapped 1-cells of the domain 2-category, i.e. $m_B\cdot Gf=Hf\cdot m_A$ (where $\cdot$ is whiskering).

A 2-functor $F:\mathcal{K}\to\mathbf{Cat}$ is called representable, when there exists a 2-natural isomorphism $$\alpha:\mathcal{K}(K,-)\xrightarrow{\quad\sim\quad}F.$$ The components of this isomorphism are $\alpha_A:\mathcal{K}(K,A)\cong FA$ in $\mathbf{Cat}$, and the unit of the representation is the corresponding `element’ $\mathbf{1}\to FK$ via Yoneda.

For a general complete symmetric monoidal closed category $\mathcal{V}$, the usual functor category $[\mathcal{A},\mathcal{B}]$ for two $\mathcal{V}$-categories is endowed with the structure of a $\mathcal{V}$-category itself, with hom-objects ends $$[\mathcal{A},\mathcal{B}](T,S)=\int_{A\in\mathcal{A}} \mathcal{B}(TA,SA)$$ (which exist at least when $\mathcal{A}$ is small). In our context of $\mathcal{V}$=$\mathbf{Cat}$ it is not necessary to employ ends and coends at all, and the hom-category $[\mathcal{K},\mathcal{L}](G,H)$ of the functor 2-category is evidently the category of 2-natural transformations and modifications. However, we note that computations via (co)ends simplify and are essential for constructions and (co)completeness results for enrichment in general monoidal categories.

The definition of weighted limits for 2-categories

To briefly motivate the definition of a weighted limit, recall that an ordinary limit of a ($\mathbf{Set}$-) functor $G:\mathcal{P}\to\mathcal{C}$ is characterized by an isomorphism $$\mathcal{C}(C,limG)\cong[\mathcal{P},\mathcal{C}](\Delta C, G)$$ natural in $C$, where $\Delta C:\mathcal{P}\to\mathcal{C}$ is the constant functor on the object $C$. In other words, the limit is the representing object of the presheaf $$[\mathcal{P},\mathcal{C}](\Delta -,G):\mathcal{C}^\op\to\mathbf{Set}.$$ Since components of a natural transformation $\Delta C\Rightarrow G$ (i.e. cones) can be viewed as components of a natural $\Delta\mathbf{1}\Rightarrow\mathcal{C}(C,G-):\mathcal{C}\to\mathbf{Set}$, the above defining isomorphism can be written as $$\mathcal{C}(C,\mathrm{lim}G)\cong[\mathcal{P},\mathbf{Set}](\Delta\mathbf{1},\mathcal{C}(C,G-)).$$ In this form, ordinary limits can be easily seen as particular examples of conical indexed limits for $\mathcal{V}$=$\mathbf{Set}$, and we are able to generalize the concept of a limit by replacing the functor $\Delta\mathbf{1}$ by an arbitrary functor (weight) $\mathcal{C}\to\mathbf{Set}$.

We may thus think of a 2-functor $F:\mathcal{P}\to\mathbf{Cat}$ as a (small) indexing type or weight, and a 2-functor $G:\mathcal{P}\to\mathcal{K}$ as a diagram in $\mathcal{K}$ of shape $\mathcal{P}$: $$\begin{matrix} & \mathbf{Cat}\quad \\ {}^{weight} \nearrow_{F} & \\ \mathcal{P} & \overset{G}\underset{diagram}{\rightarrow} & \mathcal{K}. \\ \end{matrix}$$ The 2-functor $G$ gives rise to a 2-functor $$\int_p [Fp,\mathcal{K}(-,Gp)]=[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(-,G)):\; \mathcal{K}^\op\longrightarrow\mathbf{Cat}$$ which maps a 0-cell $A$ to the category $[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(A,G))$. A representation of this contravariant 2-functor is an object $\{F,K\}\in\mathcal{K}$ along with 2-natural isomorphism $$\mathcal{K}(-,\{F,G\})\xrightarrow{\;\sim\;}[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(-,G))$$ with components isomorphisms between categories $$\mathcal{K}(A,\{F,G\})\cong[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(A,G-)).$$ The unit of this representation is $\mathbf{1}\to[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(\{F,G\},G))$ which corresponds uniquely to a 2-natural transformation $\xi:F\Rightarrow\mathcal{K}(\{F,G\},G)$.

Via this 2-natural isomorphism, the object $\{F,G\}$ in $\mathcal{K}$ satisfies a universal property which can be expressed in two levels:

• The 1-dimensional aspect of the universal property states that every natural transformation $\rho$ factorizes as $$\begin{matrix} F \xrightarrow{\rho} & \mathcal{K}(A,G) \\ {}_\xi \searrow & \uparr_{\mathcal{K}(h,1)} \\ & \mathcal{K}(\{F,G\},G) \\ \end{matrix}$$ for a unique 1-cell $h:A\to\{F,G\}$ in $\mathcal{K}$, where the vertical arrow is just pre-composition with $h$.

• The 2-dimensional aspect of the universal property states that every modification $\theta:\rho\Rrightarrow\rho'$ factorizes as $\mathcal{K}(\alpha,1)\cdot \xi$ for a unique 2-cell $\alpha:h\Rightarrow h'$ in $\mathcal{K}$.

The fact that the 2-dimensional aspect (which asserts an isomorphism of categories) does not in general follow from the 1-dimensional aspect (which asserts a bijection between the hom-sets of the underlying categories) is a recurrent issue of the paper. In fact, things would be different if the underlying category functor $$\mathcal{V}(I,-)=(\;)_0:\mathcal{V}\text{-}\mathbf{Cat}\to\mathbf{Cat}$$ were conservative, in which case the 2-dimensional universal property would always imply the 1-dimensional one. Certainly though, this is not the case for $\mathcal{V}$=$\mathbf{Cat}$: the respective functor discards all the 2-cells and is not even faithful. However, if we know that a weighted limit exists, then the first level of the universal property suffices to detect it up to isomorphism.

Completeness of 2-categories

A 2-category $\mathcal{K}$ is complete when all limits $\{F,G\}$ exist. The defining 2-natural isomorphism extends the mapping $(F,G)\mapsto\{F,G\}$ into a functor of two variables (the weighted limit functor) $$\{-,-\}:[\mathcal{P},\mathbf{Cat}]^{op}\times[\mathcal{P},\mathcal{K}]\longrightarrow \mathcal{K}$$ as the left parametrized adjoint (actually its opposite) of the functor $$\mathcal{K}(-,?):\mathcal{K}^{op}\times[\mathcal{P},\mathcal{K}]\to[\mathcal{P},\mathbf{Cat}]$$ mapping an object $A$ and a functor $G$ to $\mathcal{K}(A,G-)$. A colimit in $\mathcal{K}$ is a limit in $\mathcal{K}^op$, and the weighted colimit functor is $$-\ast-:[\mathcal{P}^op,\mathbf{Cat}]\times[\mathcal{P},\mathcal{K}]\longrightarrow\mathcal{K}.$$ Apart from the evident duality, we observe that often colimits are harder to compute than limits. This may partially be due to the fact that $\{F,G\}$ is determined by the representable $\mathcal{K}(-,\{F,G\})$ which gives generalized elements of $\{F,G\}$, whereas the description of $\mathcal{K}(F\ast G,-)$ gives us arrows out of $F\ast G$. For example, limits in $\mathbf{Cat}$ are easy to compute via $$[\mathcal{A},\{F,G\}]\cong[\mathcal{P},\mathbf{Cat}](F,[\mathcal{A},G-])\cong[\mathcal{A},[\mathcal{P},\mathbf{Cat}](F,G)]$$ and in particular, taking $\mathcal{A}=\mathbf{1}$ gives us the objects of the category $\{F,G\}$ and $\mathcal{A}=\mathbf{2}$ gives us the morphisms. On the contrary, colimits in $\mathbf{Cat}$ are not straightforward (except than their property $F\ast G\cong G\ast F$).

Notice that like ordinary limits are defined, via representability, in terms of limits in $\mathbf{Set}$, we can define weighted limits in terms of limits of representables in $\mathbf{Cat}$: $$\mathcal{K}(A,\{F,G\})\cong\{F,\mathcal{K}(A,G-)\},\quad\mathcal{K}(F\ast ,G,A)\cong\{F,\mathcal{K}(G-,A)\}.$$ On the other hand, if the weights are representables, via Yoneda lemma we get $$\{\mathcal{P}(P,-),G\}\cong GP, \qquad \mathcal{P}(-,P)\ast G\cong GP.$$

The main result for general $\mathcal{V}$-completeness in Kelly’s book says that a $\mathcal{V}$-enriched category is complete if and only if it admits all conical limits (equivalently, products and equalizers) and cotensor products. Explicitly, conical limits are those with weight the constant $\mathcal{V}$-functor $\Delta I$, whereas cotensors are those where the domain enriched category $\mathcal{P}$ is the unit category $\mathbf{1}$, hence the weight and the diagram are determined by objects in $\mathcal{V}$ and $\mathcal{K}$ respectively. Once again, for $\mathcal{V}$=$\mathbf{Cat}$ an elementary description of both limits is possible.

Notice that when a 2-category admits tensor products of the form $\mathbf{2}\ast A$, then the 2-dimensional universal property follows from the 1-dimensional for every limit, because of conservativity of the functor $\mathbf{Cat}_0(\mathbf{2},-)$ and the definition of tensors. Moreover, the former also implies that the category $\mathbf{2}$ is a strong generator in $\mathbf{Cat}$, hence the existence of only the cotensor $\{\mathbf{2},B\}$ along with conical limits in a 2-category $\mathcal{K}$ is enough to deduce 2-completeness.

$\mathbf{Cat}$ itself has cotensor and tensor products, given by $\{\mathcal{A},\mathcal{B}\}=[\mathcal{A},\mathcal{B}]$ and $\mathcal{A}\ast\mathcal{B}=\mathcal{A}\times\mathcal{B}$. It is ultimately also cocomplete, all colimits being constructed from tensors and ordinary colimits in $\mathbf{Cat}_0$ (which give the conical limits in $\mathbf{Cat}$ by the existence of the cotensor $[\mathbf{2},B]$).

If we were to make use of ends and coends, the explicit construction of an arbitrary 2-(co)limit in $\mathcal{K}$ as the (co)equalizer of a pair of arrows between (co)products of (co)tensors coincides with $$\{F,G\}=\int_K \{FK,GK\}, \qquad F\ast G=\int^K FK\ast GK.$$ Such an approach simplifies the proofs of many useful properties of limits and colimits, such as $$\{F,\{G,H\}\}\cong\{F\ast G,H\},\;\;(G\ast F)\ast H\cong F\ast(G\ast H)$$ for appropriate 2-functors.

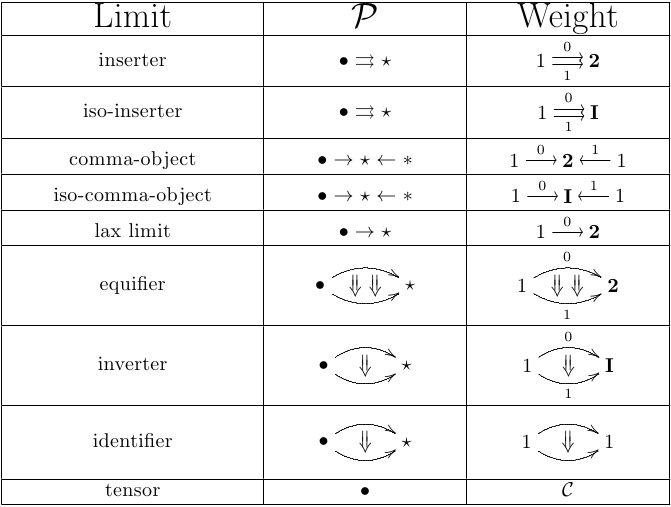
Famous finite 2-limits

The paper provides the description of some important classes of limits in 2-categories, essentially by exhibiting the unit of the defining representation for each particular case. A table which summarizes the main examples included is the following:

Let’s briefly go through the explicit construction of an inserter in a 2-category $\mathcal{K}$. The weight and diagram shape are as in the first line of the above table, and denote by $B\overset{f}\underset{g}{\rightrightarrows}C$ the image of the diagram in $\mathcal{K}$. The standard technique is to identify the form of objects and morphisms of the functor 2-category $[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(A,G-))$, and then state both aspects of the universal property.

An object is a 2-natural transformation $\alpha:F\Rightarrow\mathcal{K}(A,G-)$ with components $\alpha_\bullet:1\to\mathcal{K}(A,B)$ and $\alpha_\star:\mathbf{2}\to\mathcal{K}(A,C)$ satisfying the usual naturality condition (2-naturality follows trivially, since $\mathcal{P}$ only has the identity 2-cell). This amounts to the following data:

• an 1-cell $A\xrightarrow{\alpha_\bullet}B$, i.e. the object in $\mathcal{K}(A,B)$ determined by the functor $\alpha_\bullet$;

• a 2-cell ${\alpha_\star0}\overset{\alpha_\star}{\Rightarrow}{\alpha_\star1}$, i.e. the morphism in $\mathcal{K}(A,C)$ determined by the functor $\alpha_\star$;

• properties, which make the 1-cells $\alpha_\star0,\alpha_\star1$ factorize as $\alpha_\star0=A\xrightarrow{\alpha_\bullet}B\xrightarrow{f}C$ and $\alpha_\star1=A\xrightarrow{\alpha_\bullet}B\xrightarrow{g}C$.

We can encode the above data by a diagram $$\begin{matrix} & B & \\ {}^{\alpha_\bullet} \nearrow && {\searrow}^f \\ A\; & \Downarrow{\alpha_\star}& \quad C. \\ {}_{\alpha_\bullet} \searrow && \nearrow_g \\ & B & \\ \end{matrix}$$ Now a morphism is a modification $m:\alpha\Rrightarrow\beta$ between two objects as above. This has components

• $m_\bullet:\alpha_\bullet\Rightarrow\beta_\bullet$ in $\mathcal{K}(A,B)$;

• $m_\star:\alpha_\star\Rightarrow\beta_\star$ given by 2-cells $m_\star^0:\alpha_\star0\Rightarrow{\beta_\star0}$ and $m_\star^1:\alpha_\star1\Rightarrow\beta_\star1$ in $\mathcal{K}(A,C)$ satisfying naturality $m^1_\star\circ\alpha_\star=\beta_\star\circ m^0_\star$.

The modification condition $m^0_\star=f\cdot m_\bullet$ and $m^1_\star=g\cdot m_\bullet$ gives the components of $m_\star$ as whiskered composites of $m_\bullet$. We can thus express such a modification as a 2-cell $m_\bullet$ satisfying $gm_\bullet\circ\alpha_\star=fm_\bullet\circ\beta_\star$ (graphically expressed by pasting $m_\bullet$ accordingly to the sides of $\alpha_\star,\beta_\star$).

This encoding simplifies the statement of the universal property for $\{F,G\}$, as the object of in $\mathcal{K}$ through which any natural transformation and modification uniquely factorize in an appropriate way (in fact, through the unit $\xi$). A very similar process can be followed for the identification of the other classes of limits. As an illustration, let’s consider some of these limits in the 2-category $\mathbf{Cat}$.

• The inserter of two functors $F,G:\mathcal{B}\to\mathcal{C}$ is a category $\mathcal{A}$ with objects pairs $(B,h)$ where $B\in\mathcal{B}$ and $h:FB\to GB$ in $\mathcal{C}$. A morphism $(B,h)\to(B',h')$ is an arrow $f:B\to B'$ in $\mathcal{B}$ such that the following diagram commutes: $$\begin{matrix} FB & \overset{Ff}{\longrightarrow} & FB' \\ {}_h\downarrow && \downarrow_{h'} \\ FB & \underset{Gh}{\longrightarrow} & GB'. \\ \end{matrix}$$ The functor $\alpha_\bullet=P:\mathcal{A}\to\mathcal{B}$ is just the forgetful functor, and the natural transformation is given by $(\alpha_\star)_{(B,h)}=h$.

• The comma-object of two functors $F,G$ is precisely the comma category. If the functors have also the same domain, their inserter is a subcategory of the comma category.

• The equifier of two natural transformations $\phi^1,\phi^2:F\Rightarrow G:\mathcal{B}\to\mathcal{C}$ is the full subcategory $\mathcal{A}$ of $\mathcal{B}$ over all objects $B$ such that $\phi^1_B=\phi^2_B$ in $\mathcal{C}$.

There is a variety of constructions of new classes of limits from given ones, coming down to the existence of endo-identifiers, inverters, iso-inserters, comma-objects, iso-comma-objects, lax/ oplax/pseudo limits of arrows and the cotensors $\{\mathbf{2},K\}$, $\{\mathbf{I},K\}$ out of inserters, equifiers and binary products in the 2-category $\mathcal{K}$. Along with the substantial construction of arbitrary cotensors out of these three classes, P(roducts)I(nserters)E(quifiers) limits are established as essential tools, also relatively to categories of algebras for 2-monads. Notice that equalizers are `too tight’ to fit in certain 2-categories of importance such as $\mathbf{Lex}$.

Weaker notions of limits in 2-categories

The concept of a weighted 2-limit strongly depends on the specific structure of the 2-category $[\mathcal{P},\mathbf{Cat}]$ of 2-functors, 2-natural transformations and modifications, for the 2-categories $\mathcal{P}$ and $\mathbf{Cat}$. If we alter this structure by considering lax natural transformations or pseudonatural transformations, we obtain the definition of the lax limit $\{F,G\}_l$ and pseudo limit $\{F,G\}_p$ as the representing objects for the 2-functors $$\begin{matrix} Lax[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(-,G)):\mathcal{K}^\op\to\mathbf{Cat} \\ Psd[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(-,G)):\mathcal{K}^\op\to\mathbf{Cat}. \end{matrix}$$ Notice that the functor categories $Lax[\mathcal{P},\mathcal{L}]$ and $Psd[\mathcal{P},\mathcal{L}]$ are 2-categories whenever $\mathcal{L}$ is a 2-category, hence the defining isomorphisms are again between categories as before.

An important remark is that any lax or pseudo limit in $\mathcal{K}$ can be in fact expressed as a `strict’ weighted 2-limit. This is done by replacing the original weight with its image under the left adjoint of the incusion functors $[\mathcal{P},\mathbf{Cat}]\hookrightarrow Lax[\mathcal{P},\mathbf{Cat}]$, $[\mathcal{P},\mathbf{Cat}]\hookrightarrow Psd[\mathcal{P},\mathbf{Cat}]$. The opposite does not hold: for example, inserters and equifiers are neither lax not pseudo limits.

We can relax the notion of limits in 2-categories even further, and define the bilimit $\{F,G\}_b$ of 2-functors $F$ and $G$ as the representing object up to equivalence: $$\mathcal{K}(A,\{F,G\}_b)\simeq Psd[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(A,G)).$$ This is of course a particular case of general bilimits in bicategories, for which $\mathcal{P}$ and $\mathcal{K}$ are requested to be bicategories and $F$ and $G$ homomorphism of bicategories. The above equivalence of categories expresses a birepresentation of the homomorphism $Hom[\mathcal{P},\mathbf{Cat}](F,\mathcal{K}(-,G)):\mathcal{K}^op\to\mathbf{Cat}$.

Evidently, bilimits (firstly introduced by Ross Street) may exist even when pseudo limits do not, since they require an equivalence rather than isomorphism of hom-categories. The following two results sum up the conditions ensuring whether a 2-category has all lax, pseudo and bilimits.

• A 2-category with products, inserters and equifiers has all lax and pseudo limits (whereas it may not have all strict 2-limits).

• A 2-category with biproducts, biequalizers and bicotensors is bicategorically complete. Equivalently, it admits all bilimits if and only if for all 2-functors $F:\mathcal{P}\to\mathbf{Cat}$, $G:\mathcal{P}\to\mathcal{K}$ from a small ordinary category $\mathcal{P}$, the above mentioned birepresentation exists.

Street’s construction of an arbitrary bilimit requires a descent object of a 3-truncated bicosimplicial object in $\mathcal{K}$. An appropriate modification of the arguments exhibits lax and pseudo limits as PIE limits.

These weaker forms of limits in 2-categories are fundamental for the theory of 2-categories and bicategories. Many important constructions such as the Eilenberg-Moore object as well as the Grothendieck construction on a fibration, arise as lax/oplax limits. They are also crucial in 2-monad theory, for example when studying categories of (strict) algebras with non-strict (pseudo or even lax/oplax) morphisms, which are more common in nature.