Enrichment and the Legendre–Fenchel Transform I
Posted by Simon Willerton
The Legendre–Fenchel transform, or Fenchel transform, or convex conjugation, is, in its naivest form, a duality between convex functions on a vector space and convex functions on the dual space. It is of central importance in convex optimization theory and in physics it is used to switch between Hamiltonian and Lagrangian perspectives.
Suppose that is a real vector space and that is a function then the Fenchel transform is the function defined on the dual vector space by
If you’re a regular reader then you will be unsurprised when I say that I want to show how it naturally arises from enriched category theory constructions. I’ll show that in the next post. In this post I’ll give a little introduction to the Legendre–Fenchel transform.
There is probably no best way to introduce the Legendre–Fenchel transform. The only treatment that I knew for many years was in Arnold’s book Mathematical Methods of Classical Mechanics, but I have recently come across the convex optimization literature and would highly recommend Hugo Touchette’s The Fenchel Transform in a Nutshell — my treatment here is heavily influenced by this paper. I will talk mainly about the one-dimensional case as I think that gives a lot of the intuition.
We will start, as Legendre did, with the special case of a strictly convex differentiable function ; for instance, the function pictured on the left hand side above. The derviative of is strictly increasing and so the function can be parametrized by the derivative instead of the parameter . Indeed we can write the parameter in terms of the slope , . The Legendre-Fenchel transform can then be defined to satisfy where the angle brackets mean the pairing between a vector space and its dual. In this one-dimensional case, where and are thought of as real numbers, we just have .
As is a function of we can rewrite this as So the Legendre-Fenchel transform encodes the function is a different way. By differentiating this equation you can see that the , thus we have interchanged the abcissa (the horizontal co-ordinate) and the slope. So if has derivative at then has derivative at . This is illustrated in the above picture.
I believe this is what Legendre did and then that what Fenchel did was to generalize this to non-differentiable functions.
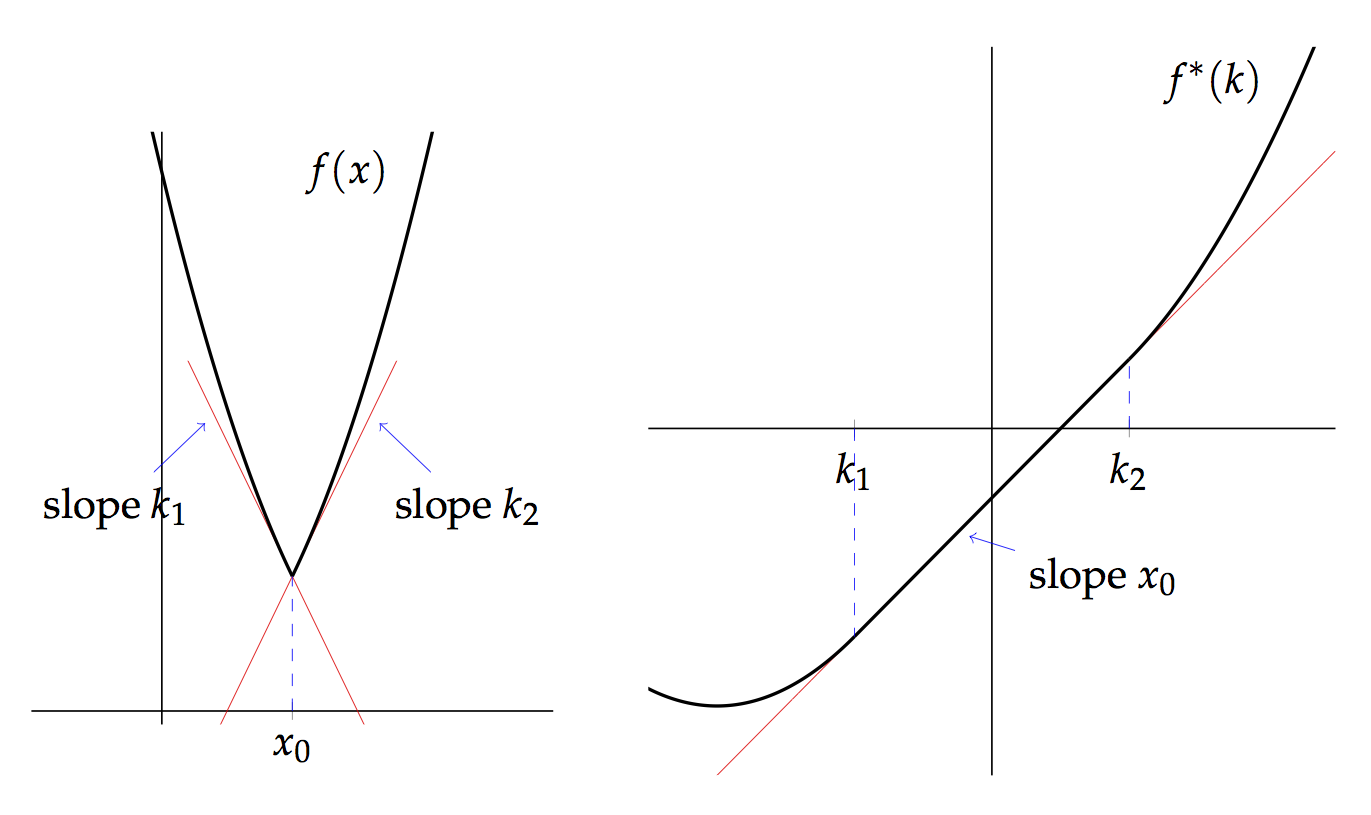
For non-differentiable functions, we can’t talk about tangent lines and derivatives, but instead can talk about supporting lines. A supporting line is one which touches the graph at at least one point and never goes above the graph. (The fact that we’re singling out lines not going above the graph means that we have convex functions in mind.)
For instance, at the point the graph pictured below has no tangent line, but has supporting lines with gradient from to . A convex function will have at least one supporting line at each point.
It transpires that the right way to generalize the transform to this non-differentiable case is to define it as follows: In this case, if has a supporting line of slope at then has a supporting line of slope at . In the picture above, at , the function has supporting lines with slope from to : correspondingly, the function has supporting lines with slope all the way from to .
If we allow the function to be not strictly convex then the transform will not alway be finite. For example, if then we have and for . So we will allow functions taking values in the extended real numbers: .
We can use the above definition to get the transform of any function , whether convex or not, but the resulting transform is always convex. (When there are infinite values involved we can also say that is lower semi-continuous, but I’ll absorb that into my definition of convex for functions taking infinite values.)
Everything we’ve done for one-dimensional easily generalizes to any finite dimensional real vector space , where we should say ‘supporting hyperplane’ instead of ‘supporting line’. From that we get a transform between sets of functions where is the vector space dual of . Similarly, we have a reverse transform going the other way, which is traditionally also denoted with a star for we define
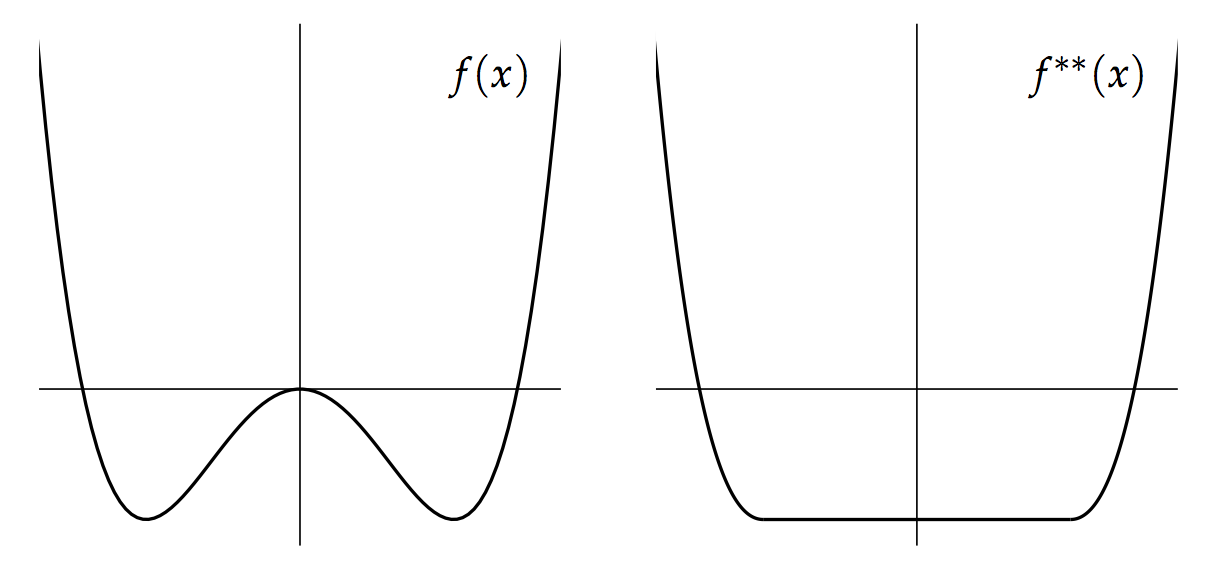
This pair of transforms have some rather nice properties, for instance, they are order reversing. We can put a partial order on any set of functions to by defining if for all . Then Also for any function we have which implies that the operator is idempotent: This means that is a closure operation. What it actually does is take the convex envelope of , which is the largest convex function less than or equal to . Here’s an example.
This gives that if is already a convex function then . And as a consequence the Legendre–Fenchel transform and the reverse transform restrict to an order reversing bijection between convex functions on and convex functions on its dual .
There are many other things that can be said about the transform, such as Fenchel duality and the role it plays in optimization, but I don’t understand such things to my own satisfaction yet.
Next time I’ll explain how most of the above structure drops out of the nucleus construction in enriched category theory.

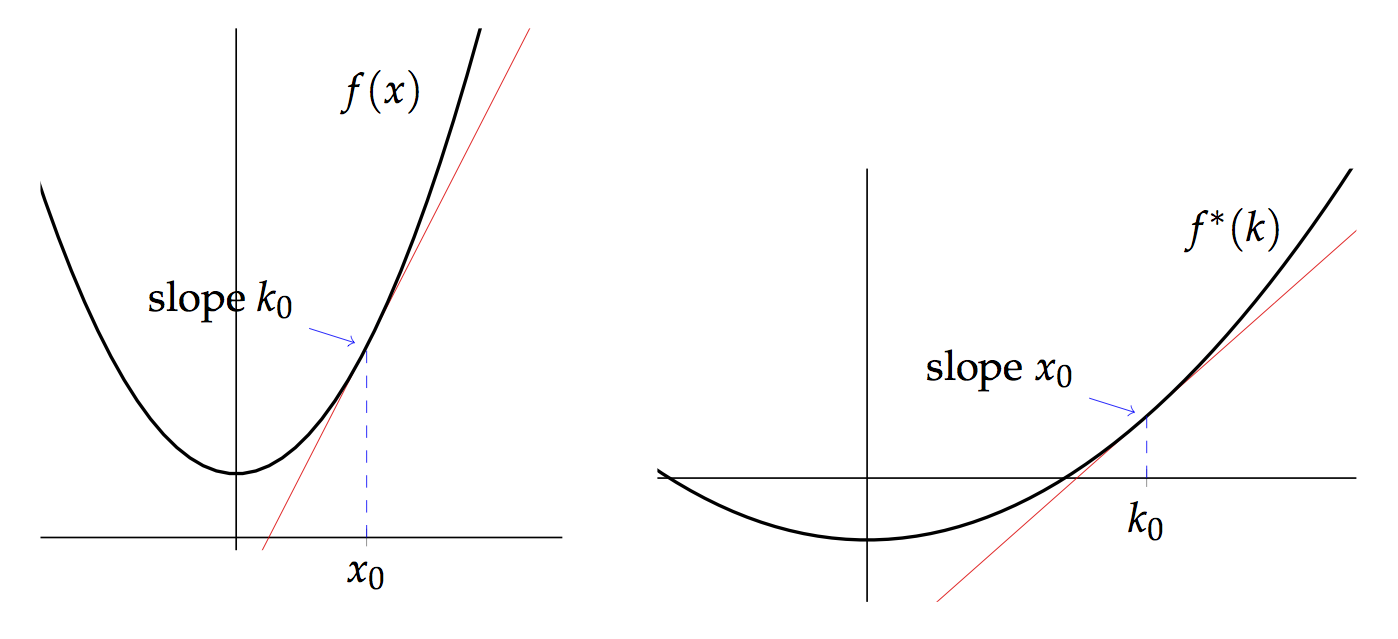
Re: Enrichment and the Legendre-Fenchel Transform I
Physics question: what’s the quantum counterpart to one’s classical Hamiltonian being convex?
I.e. what property does the “corresponding” Hermitian operator on have?