Operads and Trees
Posted by John Baez
Nina Otter is a master’s student in mathematics at ETH Zürich who has just gotten into the PhD program at Oxford. She and I are writing a paper on operads and the tree of life.
Anyone who knows about operads knows that they’re related to trees. But I’m hoping someone has proved some precise theorems about this relationship, so that we don’t have to.
By operad I’ll always mean a symmetric topological operad. Such a thing has an underlying ‘symmetric collection’, which in turn has an underlying ‘collection’. A collection is just a sequence of topological spaces for . In a symmetric collection, each space has an action of the symmetric group .
I’m hoping that someone has already proved something like this:
Conjecture 1. The free operad on the terminal symmetric collection has, as its space of -ary operations, the set of rooted trees having some of their leaves labelled .
Conjecture 2. The free operad on the terminal collection has, as its space of -ary operations, the set of planar rooted trees having some of their leaves labelled .
Calling them ‘conjectures’ makes it sound like they might be hard — but they’re not supposed to be hard. If they’re right, they should be easy and in some sense well-known! But there are various slightly different concepts of ‘rooted tree’ and ‘rooted planar tree’, and we have to get the details right to make these conjectures true. For example, a graph theorist might draw a rooted planar tree like this:
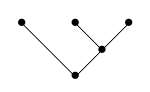
while an operad theorist might draw it like this:
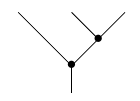
If the conjectures are right, we can use them to define the concepts of ‘rooted tree’ and ‘rooted planar tree’, thus side-stepping these details. And having purely operad-theoretic definitions of ‘tree’ and ‘rooted tree’ would make it a lot easier to use these concepts in operad theory. That’s what I want to do, ultimately. But proving these conjectures, and of course providing the precise definitions of ‘rooted tree’ and ‘rooted planar tree’ that make them true, would still be very nice.
And it would be even nicer if someone had already done this. So please provide references… and/or correct mistakes in the following stuff!
Rooted Trees
Definition. For any natural number , an -tree is a quadruple where:
- is a finite set whose elements are called internal vertices;
- is a finite non-empty set whose elements are called edges;
- and are maps sending any edge to its source and target, respectively.
Given , we write if is an edge such that and .
This data is required to satisfy the following conditions:
- is a bijection;
- there exists exactly one such that ;
- for any there exists a directed edge path from to : that is, a sequence of edges and vertices such that
So the idea is that our tree has as its set of vertices. There could be lots of leaves, but we’ve labelled some of them by numbers . In our pictures, the source of each edge is at its top, while the target is at bottom.
There is a root, called , but also a ‘pre-root’: the unique vertex with an edge going from it to . I’m not sure I like this last bit, and we might be able to eliminate this redundancy, but it’s built into the operad theorist’s picture here:

It might be a purely esthetic issue. Like everything else, it gets a bit more scary when we consider degenerate special cases.
I’m hoping there’s an operad whose set of -ary operations, , consists of isomorphism classes of -trees as defined above. I’m hoping someone has already proved this. And I hope someone has characterized this operad in a more algebraic way, as follows.
Definition. A symmetric collection consists of topological spaces together with a continuous action of the symmetric group on each space . A morphism of symmetric collections consists of an -equivariant continuous map for each . Symmetric collections and morphisms between them form a category .
(More concisely, if we denote the groupoid of sets of the and bijections between these as , then is the category of functors from to .)
There is a forgetful functor from operads to symmetric collections
with a left adjoint
assigning to each symmetric collection the operad freely generated by it.
Definition. Let be the terminal operad: that is, the operad, unique up to isomorphism, such that is a 1-element set for each .
The algebras of are commutative topological monoids.
Conjecture 1. There is a unique isomorphism of operads
that for each sends the unique -ary operation in to the corolla with leaves: that is, the isomorphism class of -trees with no internal vertices.
(When I say “the unique -ary operation in ”, but treating it as an operation in , I’m using the fact that the unique operation in gives an element in , and thus an operation in .)
Planar Rooted Trees
And there should be a similar result relating planar rooted trees to collections without symmetric group actions!
Definition. A planar -tree is an -tree in which each internal vertex is equipped with a linear order on the set of its children, i.e. the set .
I’m hoping someone has constructed an operad whose set of -ary operations, , consists of isomorphism classes of planar -trees. And I hope someone has characterized this operad as follows:
Definition. A collection consists of topological spaces . A morphism of collections consists of a continuous map for each . Collections and morphisms between them form a category .
(If we denote the category with natural numbers as objects and only identity morphisms between as , then is the category of functors from to .)
There is a forgetful functor
with a left adjoint
assigning to each collection the operad freely generated by it. This left adjoint is the composite
where the first functor freely creates a symmetric collection from a collection by setting , and the second freely generates an operad from a symmetric collection, as described above.
Conjecture 2. There is a unique isomorphism of operads
that for each sends the unique -ary operation in to the corolla with leaves ordered so that .
Have you seen a proof of this stuff???

Re: Operads and Trees
For the planar case, there’s something like this in Appendix E of my higher category theory book. Inevitably, my combinatorial definition of tree is not identical to yours, but I hope it would be easy to see that they’re equivalent.
In the appendix, I only sketched the proof, because although I’d written it out in full in private notes, it was so fantastically dull that I didn’t want to inflict it on anyone else.