Ends
Posted by Simon Willerton
The categorical notion of an end is something that several people have requested Catster videos for and Yemon Choi was recently asking if Tom had covered it in his new-born book. Given that I’ve got ends in my head at the moment for two different reasons, I thought I’d write a post on how I think about them.
I feel that seeing an integral sign like can cause people’s eyes to glaze over, never mind them getting confused as to whether that represents an end or a coend. So I will endeavour to avoid integral signs apart from right at the end.
My experience is that coends roam more freely in the wild than ends do, but I will focus on ends in this post. One reason that people are interested in ends is that natural transformation objects in enriched category theory are expressed as ends, but I will stay away from the enriched setting here.
Having said what I won’t do, maybe I should say what I will do. I will mainly concentrate on a few examples to demonstrate ends as universal wedges.
Functors
The input data for an end is a functor of the form . The only functors that I know people take the ends of are those of the form where are functors and is some kind of hom functor, i.e. either the usual hom (so ) or an internal hom (so ).
Here are some typical examples I’ve come across.
, where are functors.
, where
is finite-dimensional algebra over ,
is the category of finite-dimensional, complex representations of ,
is the category of complex vector spaces,
is the forgetful functor,
is the internal hom in , i.e. is the vector space of linear maps from to .
-
where is a finite group
is the internal hom of -representations and , so it is the vector space of linear maps with the -action on given by .
The main point of difference between 3 and 4 is that for an arbitrary algebra , the category of representations does not have an internal hom, but for a finite group it does. Other examples like 4 would involve representation categories of Hopf algebras or quantum groups.
Wedges
An end is a universal wedge, so I’d better say what a wedge is. A wedge for a functor is an object with a morphism for every object . These morphisms have to satisfy a naturality condition which says that for every morphism in , the two obvious maps you can make are the same, i.e. the following diagram commutes. We can denote such a wedge by writing .
Let’s have a look a what wedges are in the examples given above.
For , a wedge is a set and a function for each . This means that for each we get a family of morphisms . The naturality condition ensures that these are the components of a natural transformation of the identity functor . So a wedge is a set with a function .
For , by a similar argument to that above, a wedge is a set with a function to the set of natural transformations.
In this case, where we have a -algebra , an end is a vector space with a morphism for every representation of , in other words a linear map . The naturality condition says that these linear ‘action maps’ must commute with all -intertwining maps.
In the case of the internal hom of representations of a finite group, a wedge consists of a representation together with a natural ‘action’ on every -representation: . These action maps are intertwiners and must commute with all other intertwiners.
If is of the form as in 1, 3 and 4 above, then we have morphisms so in some sense is acting on for every .
Ends
An end is a universal wedge. An end for consists of a set with a morphism for each , satisfying the wedge naturality conditions, such that if is another wedge for then there is unique map such that the components of factor through as .
An end is often written as an integral . Coends, which I’m not talking about here, are written with the limits at the top of the integral sign: in Sheffield we have the mnemonic
“The end of the walking stick is at the bottom.”
I have mixed feelings about this notation. I think that people can be intimidated by it, also people get the impression that it is supposed to be something to do with integration which confuses them (or maybe that’s just me!)
We can look back at our examples and identify the ends.
For , from what is written above, it should be clear that the end is the set of natural transformations of the identity . This set is sometimes called the Hochschild cohomology of the category.
For , similar to the example above, the end is the set of natural transformations from to .
In the case of the representation category of an algebra we find that the end is actually (the underlying vector space of) the algebra itself. It is pretty obvious that the tautological action on -representations gives rise to a wedge. It is less obvious that it is the universal wedge.
This is the example of the internal hom for the representations of a finite group . Whilst we have the tautological action for every representation , we can make these into intertwining maps by taking the group algebra with the adjoint action . The resulting morphisms in make the group algebra into a wedge for the internal hom . In fact it is an end for the internal hom. This is related to the fact that a group algebra is semisimple and that there is an isomorphism of algebras in the representation category where sum runs over (a set of representatives of the equivalence classes of) the irreducible representations of .
Example 3 is the prototypical example of Tannakian reconstruction. We start with the representation category and the ‘fibre functor’ , then reconstruct from there. See the nlab page on Tanaka duality for more details.
Example 4 is a kind of ‘internal reconstruction’. More generally, for a Hopf algebra the end of the internal hom is a version of inside its category of representations. I believe that this idea is due to Shahn Majid (see Chapter 9 of Foundations of Quantum Group Theory).
Ends as Algebras (or Monoids, if you prefer)
In Examples 1, 3 and 4, the end could actually be given more structure than that of being just a set, a vector space or a representation. In all three examples the end is actually an algebra (or monoid, if you prefer) in the appropriate category. In fact, in Example 4 the end has a Hopf algebra structure, but I won’t go into that here.
Suppose the functor is of the form for some functor and for either internal or external hom then using the composition of the hom, for each we have the composite and you can check that this gives a wedge . Thus by the universal nature of the end we get a canonical map In a similar vein we have an identity morphism for each these give rise to a wedge so by the universality of we get a canonical map You can verify that and make the end into an algebra object in , and the components of the end are algebra homomorphisms.
Further examples
Just to finish we can have a look at how taking different ends on a similar category give different but related answers. So let’s look at Examples 1, 3 and 4 for the category of representations of a finite group.
If we use the ordinary hom then we get the centre of the group algebra.
If we use the internal hom in we get the group algebra.
If we use the internal hom then we get the group algebra with the adjoint action.
There ends my introduction to ends.

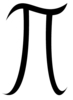

Re: Ends
Item 2 in the list of examples of ends is the same as item 2 in the list of examples of wedges. I presume that it is meant to say that the end in question is .