Cospans and Computation - Part 3
Posted by John Baez
guest post by Angeline Aguinaldo and Anna Knörr as part of the Adjoint School for Applied Category Theory 2021
Synthesi and Socrates are back! What have they learnt from Part 2 in our series of blog posts on computing with cospans?
Socrates: What an enthralling visit to the world of network security this has been!
Synthesi: I am glad you enjoyed the excursion. Any thoughts you wish to offer?
Socrates: Let us reflect on the cognitive steps we took during the last hour, as we witnessed the power of pushout composition in answering the crucial question: “Can computer A access computer B via computer C?”.

Synthesi: A suggestion I gladly second. Distilling these steps with clarity might facilitate similar applications outside of the hospital scenario.
Socrates: And to this end, will you mirror my cognitive approach with a categorical perspective?
Synthesi: Wholeheartedly, Socrates.
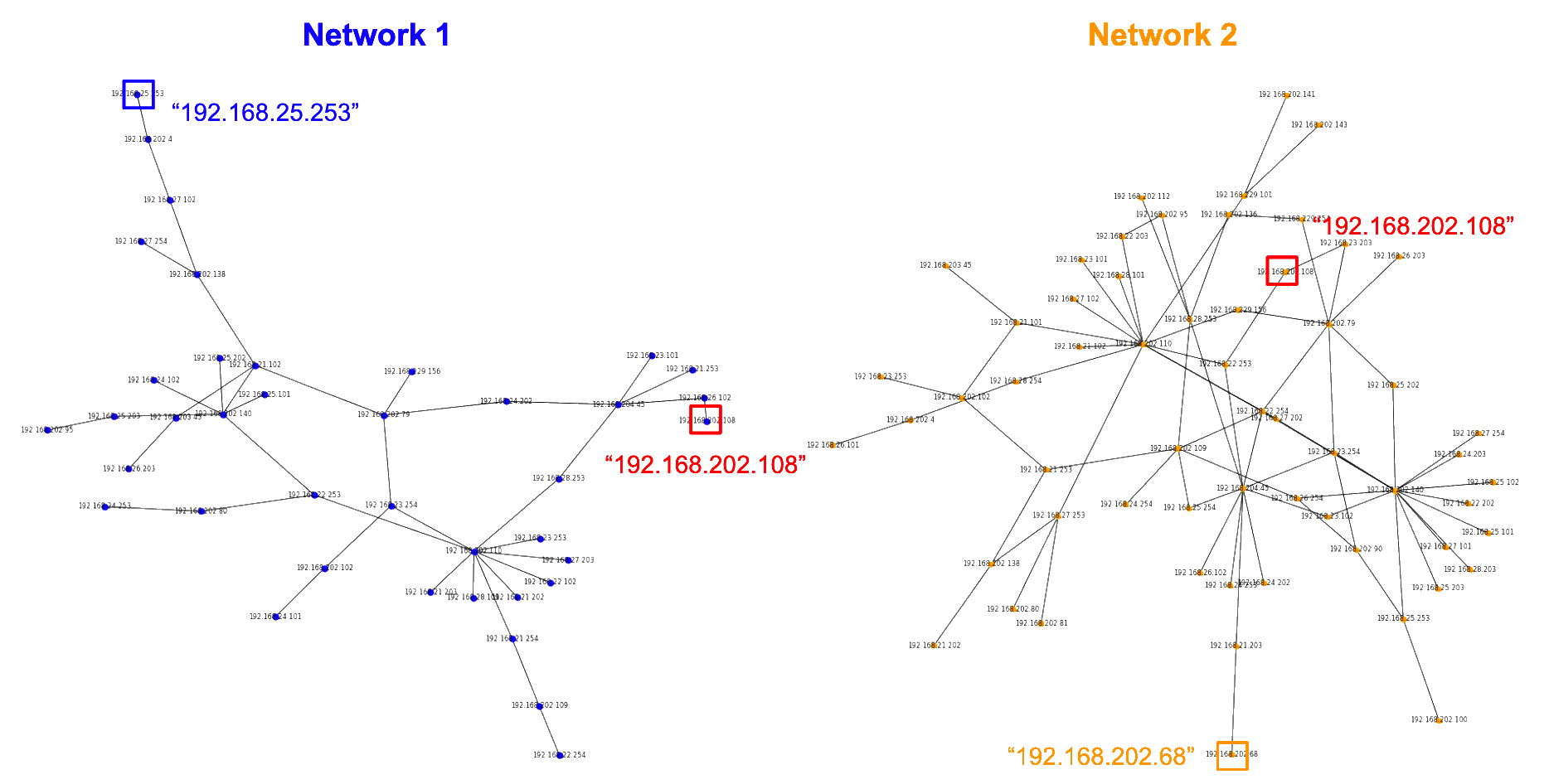
Socrates: So, as the basis for solving the security emergency, two datasets were obtained? Representing two networks of SSH connections as I believe they were called?
Synthesi: Precisely so. Picking two objects from the category of FinSet is the move that has been made.
Socrates: And these datasets were then used to compute two separate graphs? Graphs depicting connections from the origin IPs to the response IPs in each network?
Synthesi: Yes, a step we can understand as defining a functor .
Socrates: Upon which our network administrator made good use of her intuition to pick a jump box ID she deemed suspicious?
Synthesi: Which corresponds to picking a span soon to form the common leg in our categorical framework.
Socrates: In which the starting IP in network 1 and the target IP in network…
Synthesi: … are matched by the input element in cospan 1 and the output element in cospan 2.

Socrates: And moving towards the overall picture, our administrator then combined the rows of datasets from both networks? Yet labels she only added to each connection iff the suspect jump box ID was not involved?
Synthesi: Indeed, a cunning step! It is a real pushout she managed to construct! A disjoint union of finite sets, quotiented by carefully chosen elements.
Socrates: A situation she could depict visually in a penultimate move? By computing the graph of this combined dataset?
Synthesi: Indeed, it was a visualization of the pushout enabled by the decorating functor’s coherence maps.
Socrates: And this tactic culminated in a final answer… Was the starting IP connected to the target IP in this carefully crafted graph? A connection only possible via the suspect jumpbox ID, by construction?
Synthesi: Indeed, computing the connected components of this graph via a coequalizer finally confirmed her suspicion:: “192.168.25.253 is connected to 192.168.202.68 via jumpbox ID 192.168.202.108”.
Socrates: Synthesi, I thank you for this dialogue.
Synthesi: I thank you, too, dear Socrates.

Re: Cospans and Computation - Part 3
A good overview of the work has been done on the previous Post and an excellent dialogue between Socrates and Synthesi.
An interesting and necessary table comparing cognitive actions and category constructions.
Synthesi correctly notes: Indeed, a cunning step! It is a real pushout she managed to construct!. I would also add coequalizer here.
I would like to share my opinion on the topic, Categories and Network Security. The topic is more than relevant and complex, since deep knowledge of cybersecurity issues is required at the same time. I hope that you continue developing this area, regardless of when new and practically applicable results are obtained. Perhaps primarily, a more extensive use of the kospan design will be required, and secondly, the attraction of other categorical structures.