Elementary Petri nets are the objects of a category $\mathbf{N}\mathcal{C}$ whose morphisms can represent simulations or refinements of them. The interpretations of the linear logic connectives of the dialectica category $\mathbf{G}\mathcal{C}$ can be lifted to the category $\mathbf{N}\mathcal{C}$ and used to define compound nets. Each connective gives a different interpretation to the corresponding compound net, based on its meaning in intuitionistic linear logic.

The scope of the paper is wider and it covers markings, a definition of a category of arbitrary Petri nets and the description of $\mathbf{N}\mathcal{C}$ for some $\mathcal{C}$ different from $\mathbf{Set}$. We will focus on the aspect of composition of Petri nets via logical connectives giving a concrete example for each one of them and trying to give an interpretation to their corresponding constructs on Petri nets.

Preliminary definitions

Petri nets

We start by introducing Petri nets and elementary Petri nets, which will be the focus of this post.

Petri nets describe systems where some processes, called events, can be fired when all their preconditions are marked with at least the amount of tokens indicated by the weight of each arrow. After an event has been fired, the markings of all postconditions of this event will be increased by the weight of each arrow. We will represent events with rectangles and conditions with circles. The following figure represents the firing of the event $e_1$. Its preconditions, $b_0$ and $b_1$, are indicated with an incoming arrow together with a weight. Similarly, its postconditions, $b_0$ and $b_2$, are indicated with an outgoing arrow together with a weight. The firing of $e_1$ consumes a token from $b_0$ and two tokens from $b_1$ and produces one token in $b_0$ and three tokens in $b_2$.

A Petri net $\mathcal{N}= (E,B, \mathit{pre}, \mathit{post})$ is given by two sets $E, B$ and two multirelations $\mathit{pre},\mathit{post} \colon E \rightarrow _m B$. The set $E$ represents the events that are possible in the net $\mathcal{N}$ while the set $B$ represents the conditions around the events in $E$. The multirelation $\mathit{pre}$ keeps track of ”how many times” a condition is needed in order to fire an event. Similarly, the multirelation $\mathit{post}$ keeps track of ”how many times” a condition is produced after firing an event.

We will write $\mathit{pre}(e)$ and $\mathit{post}(e)$ to indicate the multisets of preconditions and postconditions of an event $e$.

In this post, we will focus on Petri nets whose $\mathit{pre}$ and $\mathit{post}$ multirelations are ordinary relations and, thus, correspond to subsets of $E \times B$. These are called elementary Petri nets.

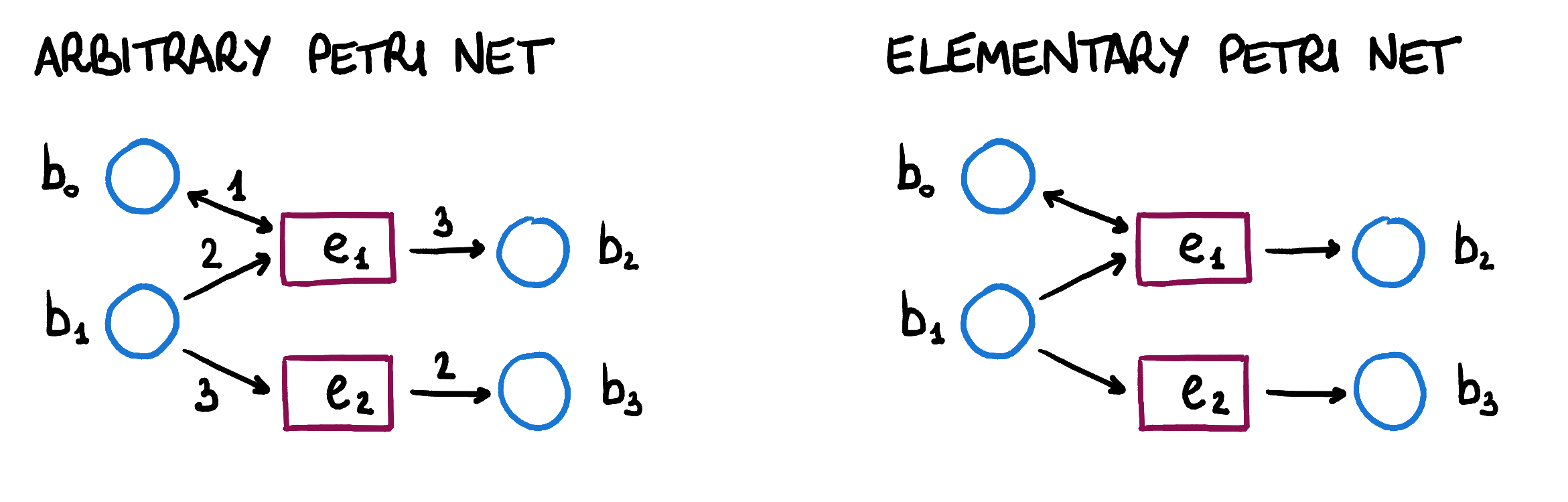
In general, the weight of each condition can be an integer. In the case of elementary Petri nets, only nets whose arrows have weight one are considered (thus, the weight is omitted).

The category of elementary Petri nets $\mathbf{N} \mathcal{C}$

We can define the category of elementary Petri nets $\mathbf{N} \mathcal{C}$ based on the dialectica category $\mathbf{G}\mathcal{C}$. Objects and morphisms in $\mathbf{N} \mathcal{C}$ are defined from objects and morphisms in $\mathbf{G} \mathcal{C}$.

Let $\mathcal{C}$ be a category with finite limits, then there is a category $\mathbf{N} \mathcal{C}$ defined as follows.

• An object is a pair $\mathcal{N}=(\mathit{pre}, \mathit{post})$, where $\mathit{pre}$ and $\mathit{post}$ are objects in $\mathbf{G}\mathcal{C}$.

• A morphism from $\mathcal{N}=(\mathit{pre}, \mathit{post})$ to $\mathcal{N}'=(\mathit{pre}', \mathit{post}')$ is a pair of morphisms $(f, F)$ in $\mathcal{C}$ such that $(f, F)$ is a morphism from $\mathit{pre}$ to $\mathit{pre}'$ and from $\mathit{post}$ to $\mathit{post}'$ in $\mathbf{G} \mathcal{C}$.

An object $\mathcal{N}=(\mathit{pre}, \mathit{post})$ of $\mathbf{NSet}$ represents an elementary Petri net whose precondition and postcondition relations are given by $\mathit{pre}$ and $\mathit{post}$. Taking $\mathcal{C} = \mathbf{Set}$ lets us explicit the conditions for $(f,F)$ to be a morphism of Petri nets. We obtain that

$$\begin{aligned} e \ \mathit{pre} \ F(b') & \Rightarrow f(e) \ \mathit{pre}' \ b'\\ e \ \mathit{post} \ F(b') & \Rightarrow f(e) \ \mathit{post}' \ b'\\ \end{aligned}$$

This means that the net $\mathcal{N}$ is a refinement of $\mathcal{N}'$. Intuitively, this means that $\mathcal{N}$ consumes and produces at least as many resources as $\mathcal{N}'$.

This is not the only way one can define morphisms of Petri net. It is possible to reverse the direction of the unique morphism $k$ for one or both the components $\mathit{pre}$ and $\mathit{post}$ of a Petri net. It is also possible to consider morphisms that give an if and only if in the condition above. All these variants have interpretations that is worth investigating. We shortly discuss the intuitions behind these variants in the last section.

The dialectica category $\mathbf{G} \mathcal{C}$

We briefly give the definition of dialectica category that is necessary to define $\mathbf{N}\mathcal{C}$. The reader already familiar with this work is invited to skip to the next section.

Given a category $\mathcal{C}$ with finite limits, we define the dialectica category $\mathbf{G} \mathcal{C}$ as follows.

• Objects are relations on objects of $\mathcal{C}$. They are given by monics $\alpha \colon A \to E \times B$ in $\mathcal{C}$. We indicate them with $\alpha \colon E \nleftarrow B$.

• A morphism $(f,F) \colon \alpha \to \alpha'$ between two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ is given by a pair of morphisms $f \colon E \rightarrow E'$ and $F \colon B' \rightarrow B$ in $\mathcal{C}$ such that there exists a (necessarily unique and monic) morphism $k$ such that the following triangle commutes.

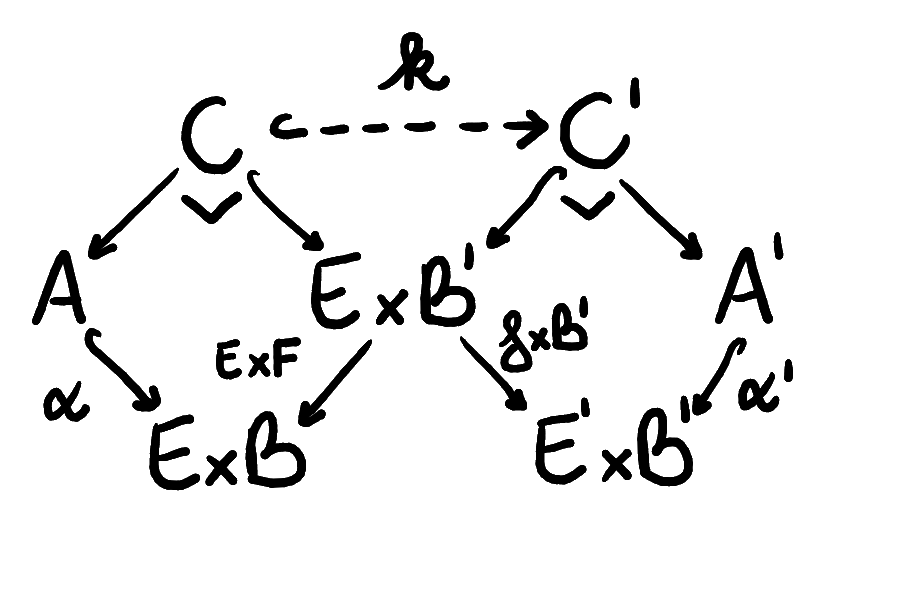
Theorem (de Paiva): If $\mathcal{C}$ is a locally cartesian closed category with finite disjoint coproducts, then $\mathbf{G}\mathcal{C}$ is a model of intuitionistic linear logic.

The structure of $\mathbf{G}\mathcal{C}$ that interprets the linear logic connectives can be lifted to the category of elementary Petri nets and used to define composites of Petri nets relying on the intuition of the linear logic connectives.

Composing Petri nets

In this section, we define how the constructs of linear logic are interpreted in $\mathbf{G} \mathcal{C}$ and, consequently, in $\mathbf{N}\mathcal{C}$. We give concrete examples in $\mathbf{NSet}$ to try to explain the intuitive meaning of these constructs on Petri nets.

Cartesian product

The cartesian product of two nets $\mathcal{N}$ and $\mathcal{N}'$ is a Petri net where events are pairs $\langle e,e' \rangle$ that represent both the events $e$, in $\mathcal{N}$, and $e'$, in $\mathcal{N}'$, happening at the same time. Conditions in the product net are conditions in $\mathcal{N}$ or in $\mathcal{N}'$.

To give a concrete example, consider two Petri nets representing interactions among genes (we took this example from a paper that uses open Petri nets for gene regulatory networks). The first one represents a gene $b_0$ that, deactivating itself, can activate gene $b_1$ or gene $b_2$, and the second one represents a gene $b_0'$ that can deactivate $b_1'$.

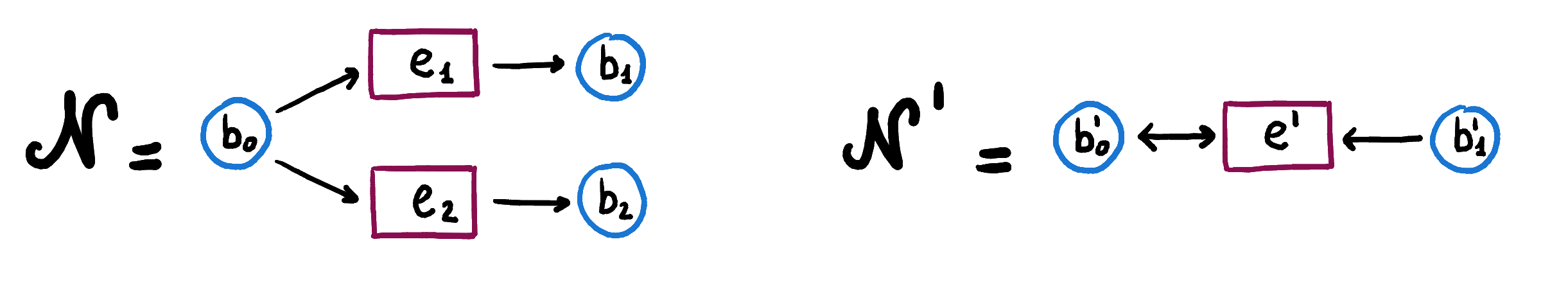
Their cartesian product represents the concurrent activation of $b_1$ or $b_2$ by $b_0$ and deactivation of $b_1'$ by $b_0'$. In fact, in order to be able to activate $b_1$ and deactivate $b_1'$ simultaneously, all the preconditions of $e_1$ in $\mathcal{N}_1$ and all the preconditions of $e'$ in $\mathcal{N}_2$ must be marked.

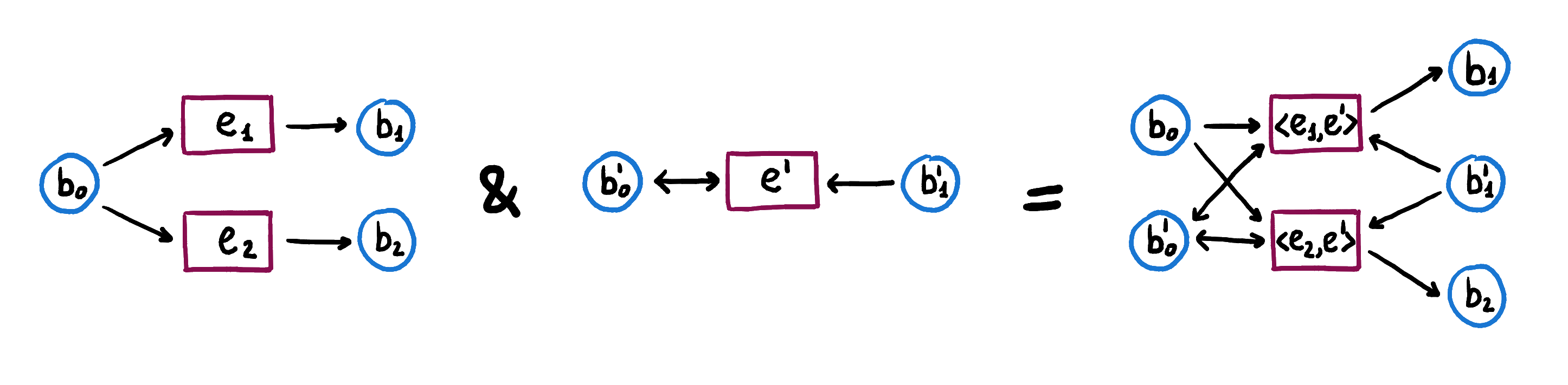
More formally, the conditions on the precondition and postcondition relations for the product $\mathcal{N} \ \& \ \mathcal{N}'$ in $\mathbf{NSet}$ are given by the union of the preconditions and postconditions in the component nets.

$$\begin{aligned} \mathit{pre}_{\&}(\langle e,e' \rangle ) & = i_{B}(\mathit{pre}(e)) \cup i_{B'}(\mathit{pre}'(e'))\\ \mathit{post}_{\&}(\langle e,e' \rangle ) & = i_{B}(\mathit{post}(e)) \cup i_{B'}(\mathit{post}'(e'))\\ \end{aligned}$$

These conditions come from the more general definition of the product in the category $\mathbf{N}\mathcal{C}$. In the category $\mathbf{N}\mathcal{C}$, the cartesian product of two nets is defined by component-wise products. $$\mathcal{N} \ \& \ \mathcal{N}' = (\mathit{pre} \ \& \ \mathit{pre}', \mathit{post}\ \& \ \mathit{post}')$$ where $\mathit{pre} \ \& \ \mathit{pre}'$ and $\mathit{post}\ \& \ \mathit{post}'$ indicate cartesian products in $\mathbf{G}\mathcal{C}$.

For the more interested reader, we present the formal definition of cartesian product in the dialectica category $\mathbf{G}\mathcal{C}$. The cartesian product of two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ in $\mathbf{G} \mathcal{C}$ is the relation $\alpha \ \& \ \alpha' \colon E \times E' \nleftarrow B + B'$ given by $$\alpha \ \& \ \alpha' = (\alpha \times \mathbb{1}_{E'})+(\alpha' \times \mathbb{1}_E)$$ where $\times$ and $+$ indicate the product and coproduct in the category $\mathcal{C}$. The projections are given by the morphisms $(\pi_{E},i_{B})$ and $(\pi_{E'},i_{B'})$.

By the universal property of the product, when $\mathcal{C}=\mathbf{Set}$, we obtain the following condition for the product relation, which directly gives the conditions for the product of Petri nets that we presented above.

$$\begin{aligned} \langle e,e' \rangle (\alpha \ \& \ \alpha')i_{B}(b) &\Leftrightarrow e \ \alpha \ b\\ \langle e,e' \rangle (\alpha \ \& \ \alpha')i_{B'}(b') &\Leftrightarrow e' \ \alpha' \ b'\\ \end{aligned}$$

Coproduct

The behaviour of a coproduct net is to be able to fire either an event in the first net or one in the second. Thus, events in the coproduct net are events from the first net or the second. Conditions are pairs of conditions in the first and second net, respectively. When a condition $\langle b,b' \rangle$ in the coproduct is marked, it is interpreted as one of the two conditions, $b$ or $b'$, is marked. We will show this through a concrete example. Consider the first of the Petri nets introduced above.

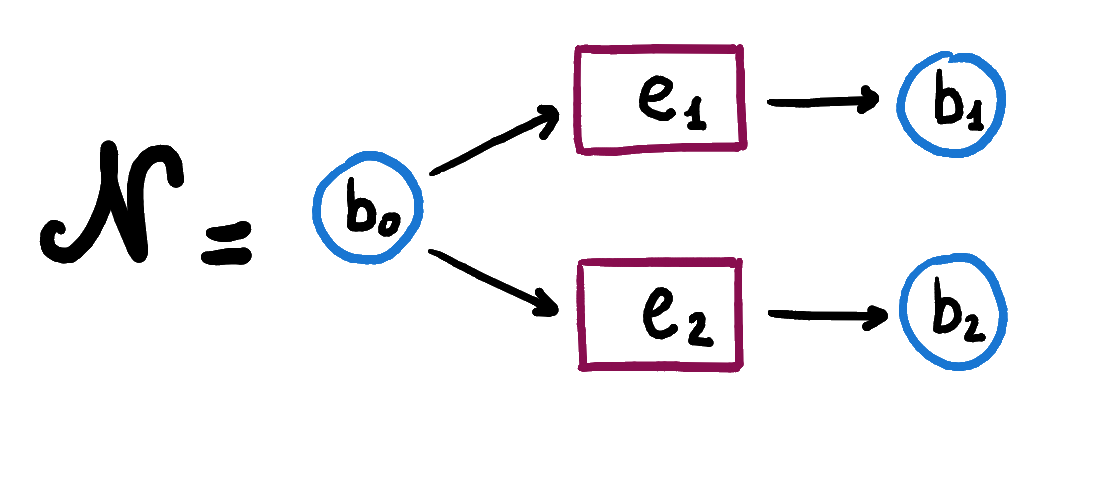
Its behaviour is to activate either $b_1$ or $b_2$ by deactivating $b_0$. This behaviour seems the one of a coproduct net as we just described it. In fact, we can see that the coproduct of the two nets $\mathcal{N}_1$, representing the activation of $b_1$, and $\mathcal{N}_2$, representing the activation of $b_2$, below is refined by the net $\mathcal{N}$.

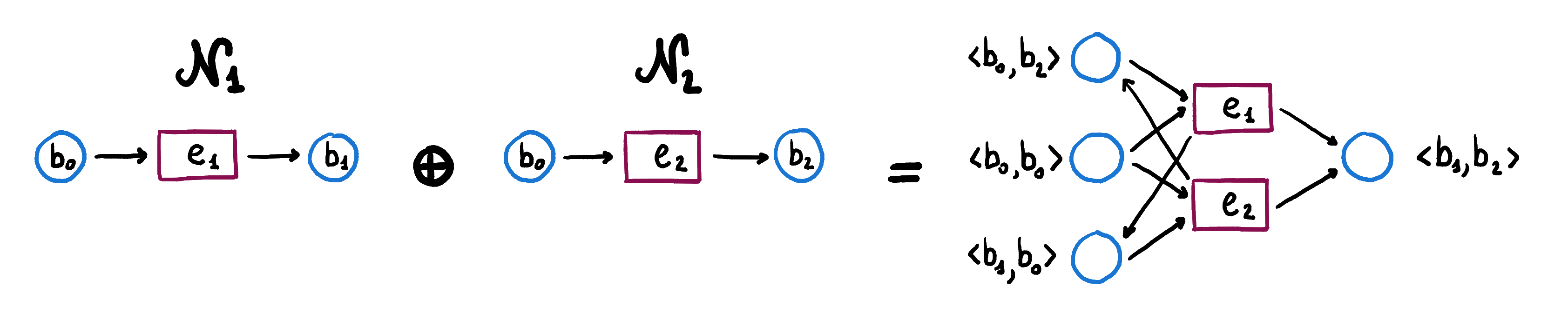
In fact, a refinement of $\mathcal{N}_1 \oplus \mathcal{N}_2$ by $\mathcal{N}$ is the morphism of elementary nets $(f,F) \colon \mathcal{N}_1 \oplus \mathcal{N}_2 \to \mathcal{N}$ given by

$$\begin{aligned} f \colon E_1 + E_2 & \to E & F \colon B & \to B_1 \times B_2 \\ e_1 & \mapsto e_1 & b_0 & \mapsto \langle b_0,b_0 \rangle \\ e_2 & \mapsto e_2 & b_1 & \mapsto \langle b_1,b_2 \rangle \\ & & b_2 & \mapsto \langle b_1,b_2 \rangle \\ \end{aligned}$$

The conditions for the coproduct of two nets $\mathcal{N} \oplus \mathcal{N}'$ in $\mathbf{NSet}$ can be given explicitly.

$$\begin{aligned} \mathit{pre}_{\oplus}(i_{E}(e)) & = \pi_{B}^{-1}(\mathit{pre}(e)) \\ \mathit{pre}_{\oplus}(i_{E'}(e')) & = \pi_{B'}^{-1}(\mathit{pre}'(e')) \\ \mathit{post}_{\oplus}(i_{E}(e)) & = \pi_{B}^{-1}(\mathit{post}(e)) \\ \mathit{post}_{\oplus}(i_{E'}(e')) & = \pi_{B'}^{-1}(\mathit{post}'(e')) \\ \end{aligned}$$

The coproduct of two nets is given by component-wise coproducts. $$\mathcal{N} \oplus \mathcal{N}' = (\mathit{pre} \oplus \mathit{pre}', \mathit{post}\oplus \mathit{post}')$$ where $\mathit{pre} \oplus \mathit{pre}'$ and $\mathit{post}\oplus \mathit{post}'$ are coproducts in $\mathbf{G}\mathcal{C}$.

We define the coproduct of two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ in $\mathbf{G} \mathcal{C}$. It is the relation $\alpha \oplus \alpha' \colon E+E' \nleftarrow B \times B'$ given by $$\alpha \oplus \alpha' = (\alpha \times \mathbb{1}_{B'})+(\alpha' \times \mathbb{1}_B)$$ where $\times$ and $+$ indicate the product and coproduct in the category $\mathcal{C}$. The inclusions are the morphisms $(i_{E},\pi_{B})$ and $(i_{E'},\pi_{B'})$.

By the universal property of the coproduct, when $\mathcal{C}=\mathbf{Set}$, we can express the coproduct relation in terms of the component relations. This gives the conditions in $\mathbf{NSet}$ written above.

$$\begin{aligned} i_{E} (e) (\alpha \oplus \alpha') \langle b,b' \rangle &\Leftrightarrow e \ \alpha \ b\\ i_{E'}(e') (\alpha \oplus \alpha') \langle b,b' \rangle &\Leftrightarrow e' \ \alpha' \ b'\\ \end{aligned}$$

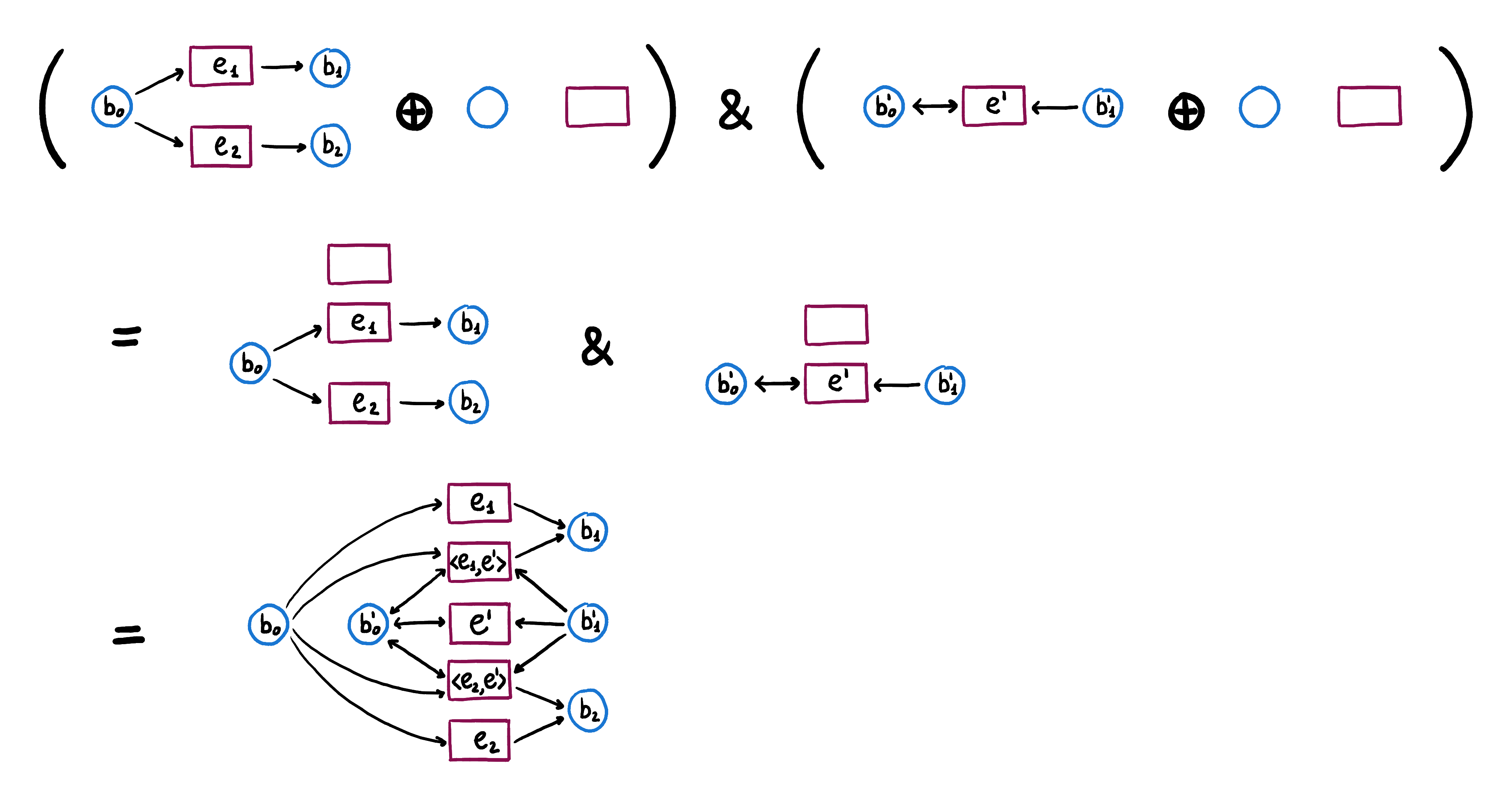
Monoidal product

The monoidal product also represents the concurrent firing of events in the two nets but, contrary to the cartesian product, it keeps track of the necessary channels of communication between events in one net and conditions in the other for the concurrent event to happen. Thus, events in $\mathcal{N} \otimes \mathcal{N}'$ are going to be again pairs of events $\langle e,e' \rangle$, with $e$ an event in $\mathcal{N}$ and $e'$ an event in $\mathcal{N}'$. However, conditions are going to be pairs of functions $\langle f,f' \rangle$ from events in one net to conditions in the other, so that $f$ represents a channel from the events in $\mathcal{N}'$ to the conditions in $\mathcal{N}$ and $f'$ a channel from the events in $\mathcal{N}$ to the conditions in $\mathcal{N}'$. Consider the monoidal product of the Petri nets shown above $\mathcal{N}$ and $\mathcal{N}'$.

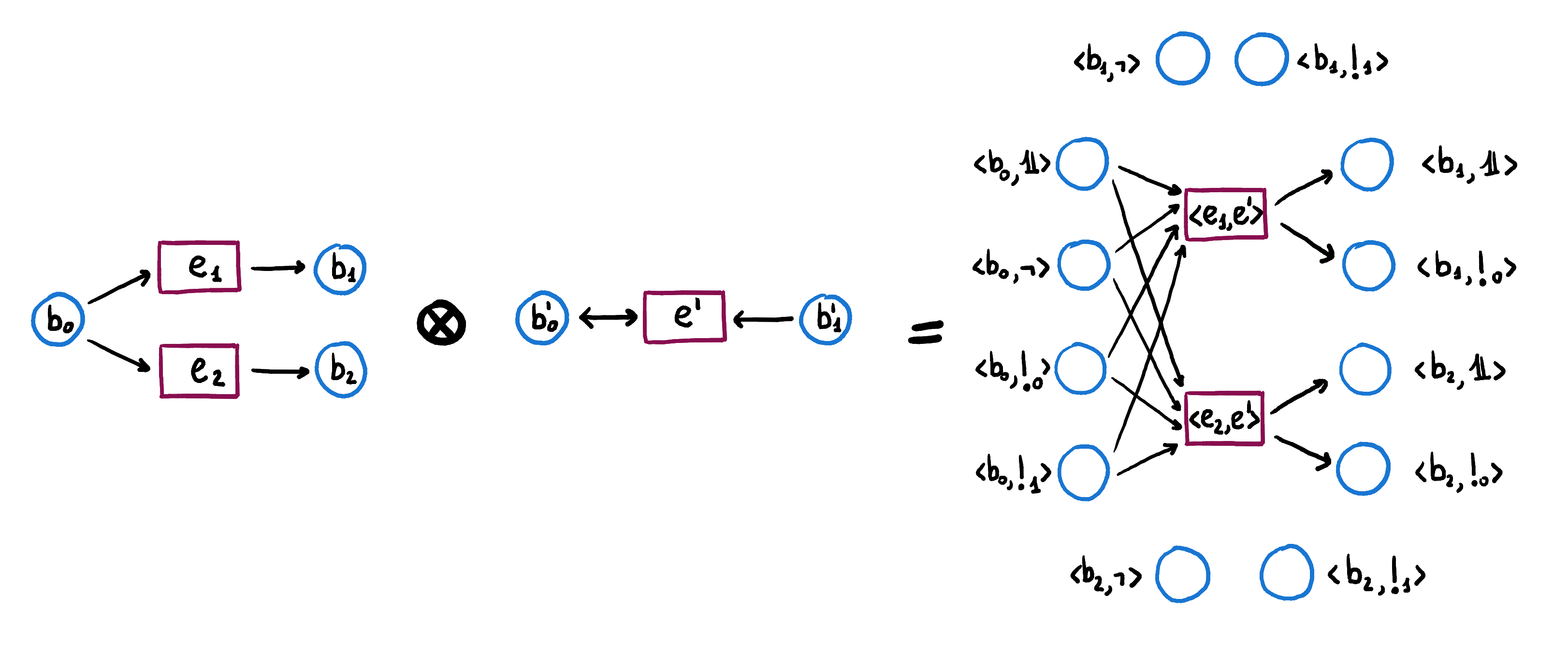
On the right hand side, we indicate with $b_i$ the function from $E'$ to $B$ that sends $e'$ to $b_i$. We indicate with $\mathbb{1}, \lnot, !_0, !_1$ the functions from $E$ to $B'$ that send $e_i$ to $b'_{i-1}$, $e_1$ to $b'_1$ and $e_2$ to $b'_0$, $e_i$ to $b_0$, and $e_i$ to $b_1$, respectively.

The preconditions for the synchronous event $\langle e_1,e' \rangle$ are all those channels that, whenever $e_1$ can fire, enable the preconditions of $e'$ and all those channels that, whenever $e'$ can fire, enable the preconditions of $e_1$. This means that the preconditions of $\langle e_1,e' \rangle$ are pairs of functions $\langle f,f' \rangle$ such that $f(e')=b_0$ and $f'(e_1) = b_0'$ or $f'(e_1) = b_1'$. Similarly, after firing $\langle e_1,e' \rangle$, the channels $\langle f,f' \rangle$ such that $f(e')=b_1$ and $f'(e_1)=b_0'$.

In $\mathbf{NSet}$, the conditions on the preconditions and postconditions sets can be given explicitly.

$$\begin{aligned} \langle e, e' \rangle \ \mathit{pre}_{\otimes} \ \langle f,f' \rangle &\Leftrightarrow e \ \mathit{pre} \ f(e') \ \text{ and } \ e' \ \mathit{pre}' \ f'(e) \\ \langle e, e' \rangle \ \mathit{post}_{\otimes} \ \langle f,f' \rangle &\Leftrightarrow e \ \mathit{post} \ f(e') \ \text{ and } \ e' \ \mathit{post}' \ f'(e) \\ \end{aligned}$$

More generally, in $\mathbf{N}\mathcal{C}$, the monoidal product of two nets is given by the component-wise monoidal product $$\mathcal{N} \otimes \mathcal{N}' = (\mathit{pre} \otimes \mathit{pre}', \mathit{post}\otimes \mathit{post}')$$ where $\mathit{pre} \otimes \mathit{pre}'$ and $\mathit{post}\otimes \mathit{post}'$ are monoidal products in $\mathbf{G}\mathcal{C}$.

For the details of this definition, we need to define the monoidal product of two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ in $\mathbf{G} \mathcal{C}$. It is the relation $\alpha \otimes \alpha' \colon E \times E' \nleftarrow B^{E^'} \times B'^E$ given by $$\alpha \otimes \alpha' = (\mathbb{1}_{E'} \times (\pi' ; \mathit{ev}_E))^{-1}(\alpha') \wedge (\mathbb{1}_{E} \times (\pi ; \mathit{ev}_{E'}))^{-1}(\alpha)$$ where $f^{-1}(g)$ indicates the pullback of $g$ along $f$ in the category $\mathcal{C}$ and $f \wedge f'$ indicates the pullback of $f$ and $f'$.

By taking $\mathcal{C} = \mathbf{Set}$, these conditions can be explicitly stated as follows.

$$\langle e, e' \rangle (\alpha \otimes \alpha') \langle f,f' \rangle \Leftrightarrow e \ \alpha \ f(e') \ \text{ and } \ e' \ \alpha' \ f'(e)$$

Units

The units of the operations given so far are the terminal object, the initial object and the monoidal unit respectively.

The unit for the cartesian product is the empty relation from $0$ to $1$, the unit of the coproduct is the empty relation from $1$ to $0$ and the monoidal unit is the identity relation from $1$ to $1$, where $0$ and $1$ indicate the initial and terminal object of $\mathcal{C}$, respectively.

Exponential

The exponential of two nets, as one might expect, gives information about the morphisms from one net to the other because morphisms from $\mathcal{N}$ to $\mathcal{N}'$ correspond to points of the exponential $\left[ \mathcal{N}, \mathcal{N}' \right]$. Events in $\left[ \mathcal{N}, \mathcal{N}' \right]$ have the types of morphisms from $\mathcal{N}$ to $\mathcal{N}'$, and they correspond to morphisms precisely when they have all places in the exponential net as preconditions and postconditions. Places in the exponential are elements in which the events can be evaluated, namely, pairs $\langle e,b' \rangle$ with $e \in E$ and $b' \in B'$. The following example shows that there is one possible morphism from the first net to the second one, the one corresponding to the coloured event $\langle ! , b_0 \rangle$.

On the right hand side, we indicate with $b_i$ the function from $B'$ to $B$ that sends $b_0'$ to $b_i$ and with $!$ the only function from $E$ to $E'$.

If the first net represents cooking pizza from the ingredients and the second net represents destroying the ingredients, then destroying the ingredients is a refinement of using the ingredients to cook a pizza and the refinement map is given by the pair of functions $(!,b_0)$ that sends cooking to destroying and the ingredients to the ingredients.

We can write the precondition and postcondition relations of the exponential of $\mathcal{N}'$ by $\mathcal{N}$ in terms of the ones in $\mathcal{N}$ and $\mathcal{N}'$.

$$\begin{aligned} \langle f,F \rangle \left[ \mathit{pre}, \mathit{pre}' \right] \langle e,b' \rangle &\Leftrightarrow \ \text{ if } \ e \ \mathit{pre} \ F(b') \ \text{ then } \ f(e) \ \mathit{pre}' \ b' \\ \langle f,F \rangle \left[ \mathit{post}, \mathit{post}' \right] \langle e,b' \rangle &\Leftrightarrow \ \text{ if } \ e \ \mathit{post} \ F(b') \ \text{ then } \ f(e) \ \mathit{post}' \ b' \\ \end{aligned}$$

More generally, in the category $\mathbf{N}\mathcal{C}$, the exponential of two nets is given by the component-wise exponential $$\left[ \mathcal{N}, \mathcal{N}' \right] = (\left[ \mathit{pre}, \mathit{pre}' \right], \left[ \mathit{post}, \mathit{post}' \right])$$ where $\left[ \mathit{pre}, \mathit{pre}' \right]$ and $\left[ \mathit{post}, \mathit{post}' \right]$ are exponentials in $\mathbf{G}\mathcal{C}$.

In the category $\mathbf{G} \mathcal{C}$, the exponential of two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ is the relation $\left[ \alpha, \alpha' \right] \colon E'^E \times B^{B'} \nleftarrow E \times B'$ given by the greatest subobject $\left[ \alpha, \alpha' \right]$ of $E'^E \times B^{B'} \times E \times B'$ such that $$\left[ \alpha, \alpha' \right] \wedge \gamma \leq \gamma'$$ with $\gamma = ((\mathbb{1}_{E'^E \times E} \times \mathit{ev}_{B'}); \pi)^{-1}(\alpha)$ and $\gamma' = ((\mathbb{1}_{B^{B'} \times B'} \times \mathit{ev}_{E}); \pi')^{-1}(\alpha')$, where $f^{-1}(g)$ indicates the pullback of $g$ along $f$ in the category $\mathcal{C}$, $f \wedgef'$ indicates the pullback of $f$ and $f'$ and $\leq$ indicates the inclusion of subobjects.

When $\mathcal{C} = \mathbf{Set}$, these conditions can be explicitly stated as follows.

$$\langle f,F \rangle \left[ \alpha, \alpha' \right] \langle e,b' \rangle \Leftrightarrow \ \text{ if } \ e \ \alpha \ F(b') \ \text{ then } \ f(e) \ \alpha' \ b'$$

Disjunctive monoidal product

The disjunctive monoidal product is the interpretation of the par connective in linear logic, whose meaning is well known to be unintuitive. Its behaviour on Petri nets is similar to the one of $\otimes$ but with disjunction instead of conjunction. Events in $\mathcal{N} \invamp \mathcal{N}'$ are pairs of functions from the conditions in one net to the events in the other, and places elements in which to evaluate the events, namely pairs $\langle b,b' \rangle$ with $b \in B$ and $b' \in B'$. We can see an example.

On the right hand side, we indicate with $e_i$ the function from $B'$ to $E$ that sends $b_0'$ to $e_i$ and with $!$ the only function from $B$ to $E'$.

In $\mathbf{NSet}$, the conditions on the preconditions and postconditions of $\mathcal{N} \invamp \mathcal{N}'$ can be given explicitly.

$$\begin{aligned} \langle f, f' \rangle \ \mathit{pre}_{\invamp} \ \langle b,b' \rangle & \Leftrightarrow f(b') \ \mathit{pre} \ b \ \text{ or } \ f'(b) \ \mathit{pre}' \ b'\\ \langle f, f' \rangle \ \mathit{post}_{\invamp} \ \langle b,b' \rangle &\Leftrightarrow f(b') \ \mathit{post} \ b \ \text{ or } \ f'(b) \ \mathit{post}' \ b' \\ \end{aligned}$$

In the category $\mathbf{N}\mathcal{C}$, the disjunctive monoidal product of two nets is given by the component-wise monoidal product $$\mathcal{N} \invamp \mathcal{N}' = (\mathit{pre} \invamp \mathit{pre}', \mathit{post}\invamp \mathit{post}')$$ where $\mathit{pre} \invamp \mathit{pre}'$ and $\mathit{post}\invamp \mathit{post}'$ are disjunctive monoidal products in $\mathbf{G}\mathcal{C}$.

In $\mathbf{G} \mathcal{C}$, the disjunctive monoidal product of two objects $\alpha \colon E \nleftarrow B$ and $\alpha' \colon E' \nleftarrow B'$ is the relation $\alpha \invamp \alpha' \colon E^{B'} \times E'^B \nleftarrow B \times B'$ given by $$\alpha \invamp \alpha' = \binom{(\mathbb{1}_{B} \times (\pi' ; \mathit{ev}_B))^{-1}(\alpha')}{(\mathbb{1}_{B'} \times (\pi ; \mathit{ev}_{B}))^{-1}(\alpha)}$$ where $f^{-1}(g)$ indicates the pullback of $g$ along $f$ in the category $\mathcal{C}$ and $\binom{f}{f'}$ indicates the unique map from the coproduct of the domains of $f$ and $f'$.

By taking $\mathcal{C} = \mathbf{Set}$, these conditions can be explicitly stated as follows.

$$\langle f,f' \rangle (\alpha \invamp \alpha') \langle b, b' \rangle \Leftrightarrow f(b') \ \alpha \ b \ \text{ or } \ f'(b) \ \alpha' \ b'$$

Negation

The unit for the disjunctive monoidal product is given by the net with one place and one event that are not related to each other.

The exponential $\left[ {\alpha}, \perp \right]$ corresponds to the negation of the relation $\alpha$. The same interpretation holds for the objects of $\mathbf{NSet}$.

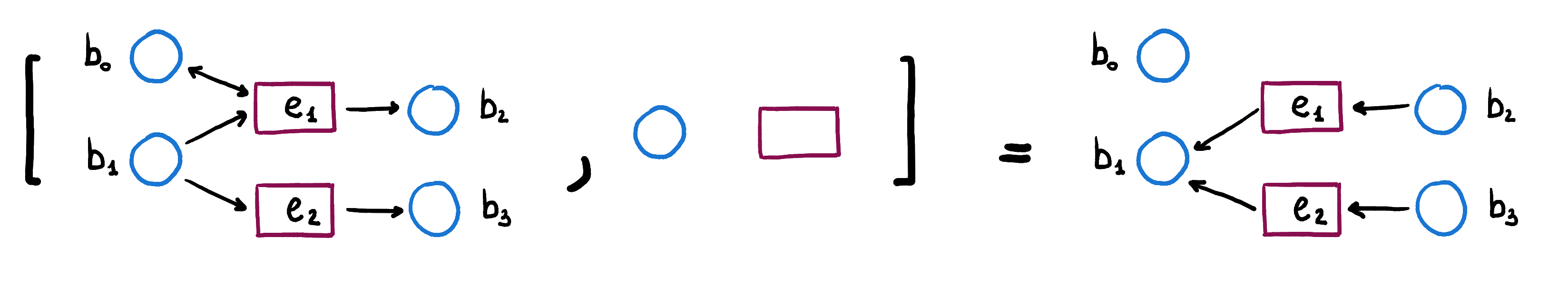
Asynchronous events

We have seen how to model events happening synchronously with the cartesian product. One may wonder how to account for the possibility for only one net to fire in the cartesian product. The idea is to allow both the nets to ”do nothing” by adding an extra ”empty” event to both the nets and, then, taking the cartesian product. This is obtained by taking the coproduct with the negation net. In fact, the net $\mathcal{N} \oplus \perp$ is the net $\mathcal{N}$ with one additional event that has no preconditions nor postconditions.

We take again the example of genes activating other genes to show how this works concretely. We compute $(\mathcal{N} \oplus \perp) \ \& \ (\mathcal{N}' \oplus \perp)$.

We see that the events in this net are pairs of events in $\mathcal{N}$ and $\mathcal{N}'$, with the same interpretation that they have in the cartesian product $\mathcal{N} \ \& \ \mathcal{N}'$, or events, like $e_1$, $e_2$ and $e'$, that represent the asynchronous events gene $b_0$ activates gene $b_1$, gene $b_0$ activates gene $b_2$ and gene $b'_0$ deactivates gene $b'_1$, respectively, happening in one net while the other net ”does nothing”.

Discussion

The challenge of this framework is to understand how it can be useful in the numerous and diverse applications of Petri nets. In order to do this, it is worth investigating different twists in the definition of the category $\mathbf{N}\mathcal{C}$. As mentioned above, it is possible to reverse the direction of the unique morphism $k$ (the one appearing in the definition of morphism in $\mathbf{G}\mathcal{C}$) in either of the components $\mathit{pre}$ or $\mathit{post}$ of a Petri net. Thus, we can get four variants of category $\mathbf{N}\mathcal{C}$, based on the four different combinations for defining morphisms in this category. By changing the direction of the morphism $k$ in the definition of morphism in the category $\mathbf{G}\mathcal{C}$, we obtain another category, isomorphic to $\mathbf{G}\mathcal{C}^{op}$, called $\mathbf{G}\mathcal{C}^{co}$. The four variants are as follows. A pair $(f, F)$ is a morphism of $\mathbf{N} \mathcal{C}$ such that:

1. $(f, F) \colon \mathit{pre} \rightarrow \mathit{pre}'$ in $\mathbf{G} \mathcal{C}$, and $(f, F) \colon \ \mathit{post} \ \rightarrow \mathit{post}'$ in $\mathbf{G}\mathcal{C}$.

2. $(f, F) \colon \mathit{pre} \rightarrow \mathit{pre}'$ in $\mathbf{G}\mathcal{C}^{co}$, and $(f, F) \colon \ \mathit{post} \ \rightarrow \mathit{post}'$ in $\mathbf{G} \mathcal{C}$.

3. $(f, F) \colon \mathit{pre} \rightarrow \mathit{pre}'$ in $\mathbf{G} \mathcal{C}$, and $(f, F) \colon \ \mathit{post} \ \rightarrow \mathit{post}'$ in $\mathbf{G}\mathcal{C}^{co}$.

4. $(f, F) \colon \mathit{pre} \rightarrow \mathit{pre}'$ in $\mathbf{G}\mathcal{C}^{co}$, and $(f, F) \colon \ \mathit{post} \ \rightarrow \mathit{post}'$ in $\mathbf{G}\mathcal{C}^{co}$.

We can explicit the conditions above in the case $\mathcal{C} = \mathbf{Set}$. For all $e$ in $E$ and all $b'$ in $B'$ we get the following inequalities.

1. $\mathit{pre}(e, F b') \leq \mathit{pre}'(f e, b')$ and $\mathit{post}(e, F b') \leq \mathit{post}'(f e, b')$. Intuitively, this can be summed up as ”more gives more”.

2. $\mathit{pre}(e, F b') \geq \mathit{pre}'(f e, b')$ and $\mathit{post}(e, F b') \leq \mathit{post}'(f e, b')$. Intuitively, this can be summed up as ”less gives more”.

3. $\mathit{pre}(e, F b') \leq \mathit{pre}'(f e, b')$ and $\mathit{post}(e, F b') \geq \mathit{post}'(f e, b')$. Intuitively, this can be summed up as ”more gives less”.

4. $\mathit{pre}(e, F b') \geq \mathit{pre}'(f e, b')$ and $\mathit{post}(e, F b') \geq \mathit{post}'(f e, b')$. Intuitively, this can be summed up as ”less gives less”.

The definition that we chose to present is the first one, given in the earlier version of the paper (where elementary Petri nets are called structurally safe), while the third variant is the same category defined in a later version of the paper. Morphisms in (1) represent refinements, while morphisms in (3) represent simulations.

It is also possible to generalise this construction to arbitrary Petri nets by taking pairs of objects of $\mathbf{G}\mathcal{C}$ of the form $E \nleftarrow B \times \mathbb{N}$ and we leave the detailed discussion of this definition as another aspect to investigate further.

We thank the organizers of the ACT school for making this blog post possible and our group, in particular our TA Jade Master for her helpful suggestions.