Partial Evaluations 2
Posted by John Baez
guest post by Carmen Constantin
This post belongs to the series of the Applied Category Theory Adjoint School 2019 posts. It is a follow-up to Martin and Brandon’s post about partial evaluations.
Here we would like to use some results by Clementino, Hofmann, and Janelidze to answer the following questions: When can we compose partial evaluations? and more generally When is the partial evaluation relation transitive?
Introduction
In this post, for simplicity, we study monads over the category of sets. A similar discussion can be had in more general categories by replacing elements of a set by generalized elements, that is, arrows into the object . See this previous blog post for more details about this.
An algebra of a monad comes equipped with a way of evaluating the expressions in via the map
This algebra map has to interact nicely with the multiplication of the monad, in particular making the coequalizer of the pair
This can be used to refine the notion of evaluation: a term is a partial evaluation of a term , written if there is a ‘one dimension higher’ term in which witnesses the partial evaluation in the sense that and in the diagram
The blue line expresses the partial evaluation relation, that is, the existence of such an element in given and . Note that, since the black arrows of the diagram above commute, a necessary condition for the existence of such is that agrees with in .
We have seen in a previous blog post that the partial evaluation relation is reflexive, and for some monads, e.g. the Free Monoid/List monad, it is also transitive: if and are witnessed by and respectively, then there is some witnessing
One could ask whether there is a term in such that and . If such a term exists, then one can simply take to be the desired witness for transitivity.
The existence of such a term corresponds to the existence of a strategy for finding a transitivity witness.
This can be summarised in the following picture:
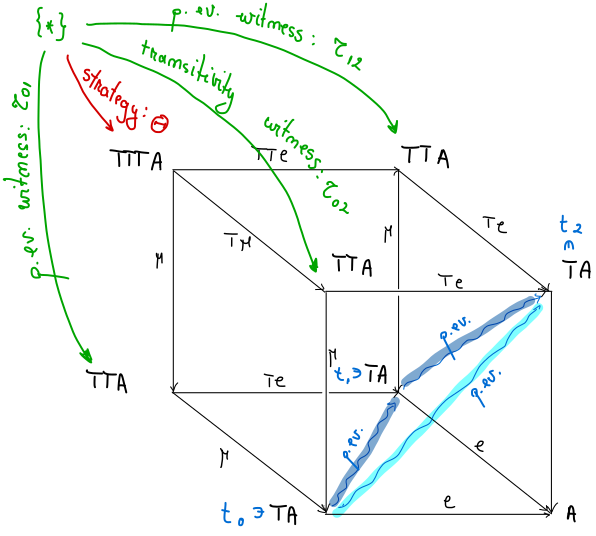
where we have indicated the existence of partial evaluations by a pair of squiggly lines highlighted in dark blue (to avoid confusion with the diagram’s actual arrows), while their composite is highlighted in light blue.
Remark 1. A strategy always exists if the back square of the cube above (which we shall refer to as ‘the monad’s cube’) is a weak pullback.
A weak pullback square is a commutative square with the existence but not necessarily the uniqueness condition of the universal property of pullbacks (see the nLab page on weak limits). Of course, a transitivity witness might exist even if there is no strategy for finding it.
Note also that the partial evaluations and their composite form a triangle, i.e. a 2-simplex, if view the bar construction as a simplicial set—see the previous blog post.
Moreover, in simplicial language, the outer green arrows correspond to the two edges forming an inner 2-horn, while the one labeled ‘transitivity witness’ is the missing edge of the horn. The existence of the strategy arrow corresponds to the existence of what is called a horn filler. As we have previously noted, a transitivity witness might exist even if there is no horn filler.
A quick intuitive example to illustrate the transitivity property is given by the free commutative monoid monad, where consists of formal sums of elements in . If , the algebra map simply evaluates a formal sum to return an element in . We can draw a picture of the terms , and which illustrates the transitivity of the partial evaluation relation .

Of course, if the partial evaluation relation is transitive, then we can think about forming even longer composites. For example, for three composable back-to-back partial evaluations (depicted in dark blue in the figure below) the existence of an associator (and hence a coherent way to compose them) would be given by a 3-simplex, i.e. a filled tetrahedron, which corresponds to an element of . This element should restrict under , , and respectively to the corresponding elements in that give the strategies for the binary composites.
This can be illustrated by a 4-dimensional cube diagram, where again dark blue lines represent the partial evaluations, light blue lines represent their binary composites and the labels of the monad’s cube have been suppressed to avoid clutter.
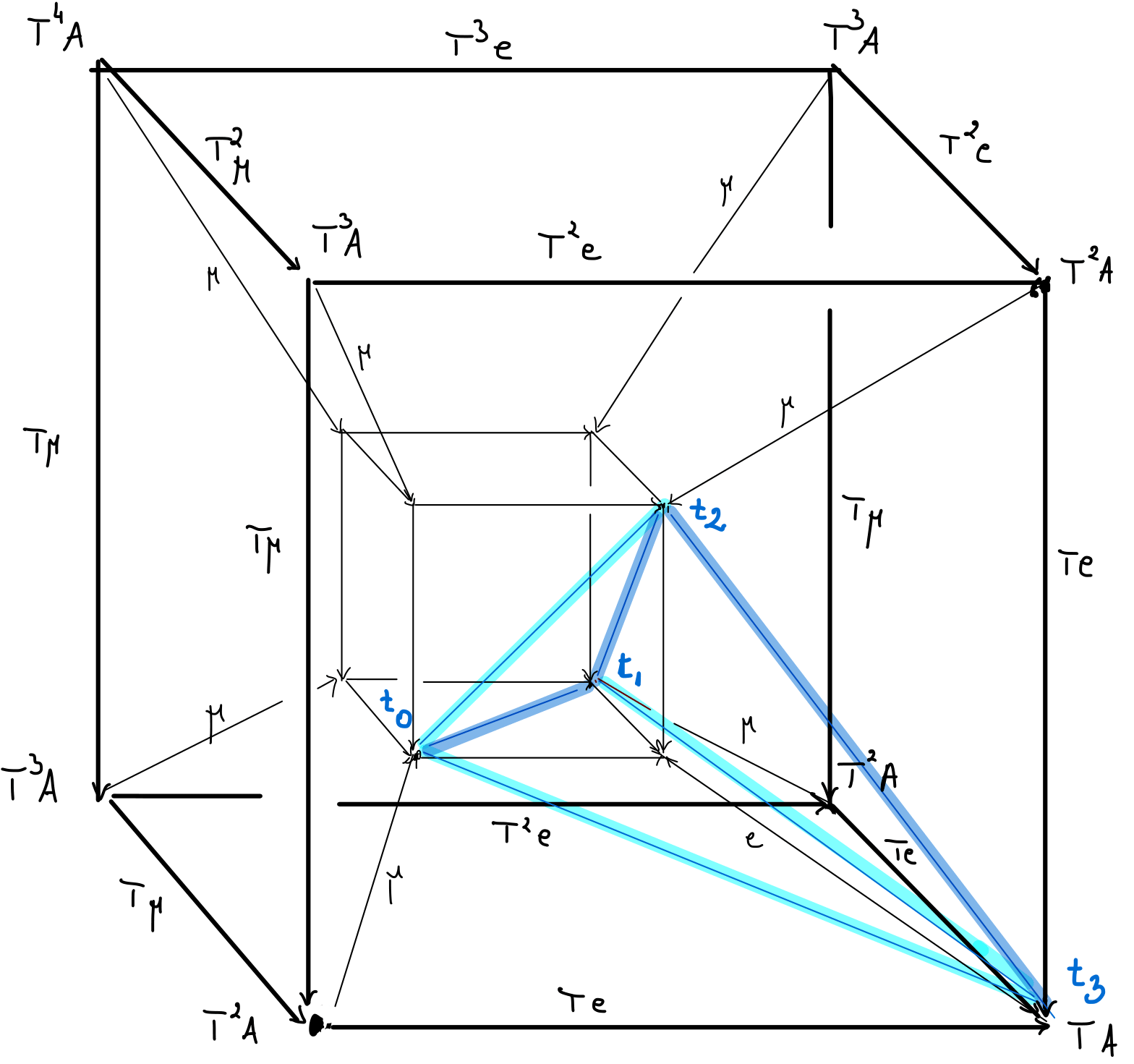
Each 3-horn corresponds to a union of all but one of the faces of the -simplex. When the omitted face is the one opposite to the first or last of the corners of the tetrahedron, one speaks of outer horns, otherwise they are called inner horns. This terminology is important because aside from transitivity, which we shall talk about in the remainder of the blog post, we have also looked at the possibility of finding horn fillers for inner horns (for monads which allow binary composites), as their existence would make the structures arising from the bar construction into a quasicategory. However, it turned out that even when binary composites exist for all composable partial evaluations, it is not always possible to find such fillers.
Weakly cartesian monads
When a monad is weakly cartesian, the partial evaluation relation is transitive. A monad is weakly cartesian if the functor preserves weak pullbacks, and all naturality squares of and are weak pullbacks. In particular the back square of the monad’s cube discussed in Remark 1 is a weak pullback, meaning that the aforementioned in exists.
Here is a well-known fact:
Remark 2. If a monad is associated to a variety of universal algebras, and the variety is operadic, then the functor is cartesian (and so, in particular, weakly cartesian).
To understand this statement note that a variety comes equipped with a monadic free-forgetful adjunction between and the category of sets, that is, the Eilenberg-Moore category of algebras for the monad is isomorphic to . Now consider a presentation of the variety , where is a signature (a set of function symbols of arbitrary but finite arity , including the constants of arity zero), and is a set of equational laws or identities between terms in . A variety is operadic if it can be presented using a set of identities which have the same variables appearing in the same order, without repetition, on each side. For example, would be an admissible identity for an operadic theory, but and would not.
Operadic (and hence cartesian) varieties include
- all varieties that can be presented with no identities, i.e. by a pair where and in particular also all varieties in which , such as sets and pointed sets.
- the variety of monoids, where only contains the monoid multiplication and is the constant representing the unit of the monoid. The identities in corresponding to the law of associativity and the unit law are clearly operadic.
- the variety of semigroups
- all varieties of the form where is a monoid, that is, of monoid actions on sets (including group actions).
The theory of groups on the other hand is not operadic: it contains the identity , which is not allowed.
Since the monads associated to these varieties are cartesian, and so weakly cartesian, for these monads the partial evaluation relation is transitive. How, then, do partial evaluations behave for monads which are not weakly cartesian?
Monads which are not weakly cartesian
The paper The monads of classical algebra are seldom weakly cartesian lists several necessary and several sufficient conditions for weak cartesianness of the functor , the unit and the multiplication respectively for monads defined over algebraic varieties in general and free semimodule monads in particular.
Notably, even if a monad is not weakly cartesian, a strategy for composing partial evaluations can be found by applying the map within the monad’s cube, as long as the square in Lemma 2 is a weak pullback—a much weaker condition than requiring weak cartesianness of as a natural transformation.
In fact we noticed that some monads which are not weakly cartesian still have transitive partial evaluations, such as the monad corresponding to the variety of -sets which satisfy the identity , which in the paper is discussed in Example 3.4.
A counterexample
The first interesting result for our project comes from the subsequent discussion in the paper, which can be used to show that counterexamples to transitivity also occur.
In particular, it is interesting to look at the free -semimodule monad (let denote this monad), where is a particular semiring. There are a number of conditions stated in the paper such that, if any of them is satisfied by the semiring , then the functor is a weakly cartesian functor:
no non-zero elements in can have an additive inverse
for every there exists such that either or
the additive monoid of is a monoid with cancellation (equivalently, it can be embedded into an abelian group).
Once is a weakly cartesian functor, the multiplication is weakly cartesian if and only if additionally
No non-zero element in has an additive inverse
has no (non-zero) zero divisors
for any generating subset of and any with such that , there exists a map with
The counterexamples we are interested in arise from semirings which satisfy the first 5 conditions but fail to satisfy the last one.
Consider for example the free semimodule monad over the semiring . This monad is given by
. To keep the presentation more intuitive, we can use a simpler notation for the elements of , writing each element as a formal sum which consists of a finite number of terms in with coefficients in . Note that two such formal sums represent the same element if and only if they have the same elements of with the same corresponding coefficients, but perhaps appearing in a different order in the expansion.
the intuitive equivalent description of the unit is then
the multiplication represents the familiar distributivity property: if then
An algebra map then simply evaluates the formal weighted sum to some element . Thus an algebra for this monad corresponds to an actual semimodule over , in the classical sense of the term.
Note that the map is then given by
where is the evaluation of the corresponding sum.
We can not only show that the back square of the monad’s cube is not a weak pullback for this monad, and hence no strategies for finding transitivity witnesses exist, but also that transitivity itself fails to hold for this monad. Let be the one element -algebra, i.e. the zero semimodule. The elements of are formal sums with just one term and the evaluation map is trivial in the sense that the value of is just , as one would expect from multiplication acting on zero. There is a partial evaluation between the terms and witnessed by the element since and also
There is also a partial evaluation between and witnessed by the element namely, and also However, there can be no partial evaluation from to because maps any in to So if were a transitivity witness, we would need But is additively indecomposable in . Hence , for some . But then which cannot equal , since is not a unit in .
Some further thoughts
It was quite satisfying to find a concrete answer to the transitivity question we started from. There are several directions that we could explore further.
On the one hand, there are interesting connections with probability which Paolo Perrone has discussed in a previous blog post, and Brandon and Martin have written about.
On the other hand, it has been pointed out to us that it is likely to find connections with multi-stage programming and partially static data structures which have been used by computer scientists to describe computations that give the programmer a fine-grained control over beta reduction. Being able to control evaluation provides a basis for optimisation of binding times.
We can also further investigate these structures by trying for example to find out when partial evaluations are invertible. Together with transitivity, this would turn the partial evaluation into an equivalence relation.
If the algebra structure square
is a weak pullback, then the partial evaluation relation is an equivalence relation. One can ask if the converse also holds.
A more sophisticated question than whether the relation being an equivalence is the following: when is the 1-truncation of the bar construction a groupoid? That is, in case we can form a category with partial evaluations as morphisms, when are all morphisms there invertible?
For example, let be a group. The theory of -sets is operadic, so the associated monad is (strongly) cartesian, and the bar construction gives the nerve of a category. The 0-simplices are the elements of , the 1-simplices from to are the elements of such that and , and so on. The partial evaluation relation here is an equivalence relation (the multiplication square is even an actual pullback – not just a weak one) and for this theory the bar construction of an algebra is the nerve of a groupoid.
This is probably very related to group cohomology: in this case, the bar construction is indeed a resolution of , i.e. weakly equivalent to . (The bar construction was actually first invented to compute the cohomology of -modules, which are basically this example, just in an abelian category.)
One can also ask higher-dimensional questions, such as when is the bar construction an infinity-groupoid (i.e. a Kan complex)?
It turns out that this last question has a partial answer which involves Mal’cev theories.
A Mal’cev operation on a set is a ternary operation such that for each , A Mal’cev theory is an algebraic theory which contains a Mal’cev operation.
In the algebraic theory of groups, there is a Mal’cev operation defined by Therefore any theory whose algebras are groups, with possibly extra structures or properties, is a Mal’cev theory. These include for example the theories of groups, rings or modules over a fixed ring but not, for example, the theory of monoids, commutative monoids, semirings, and semimodules.
An example of a Mal’cev theory which is not a theory of particular groups is the theory of heaps.
A theorem by Carboni, Kelly and Pedicchio states that for any Mal’cev theory every simplicial object in the category of algebras is a Kan complex. This theorem can be found here. See also the nLab page about Kan complexes.
Therefore, for the theory of groups (and heaps, etc.), not only do we get an equivalence relation, but the whole bar construction is an -groupoid, of which the equivalence relation is the shadow, i.e. the (0,1)-truncation.

Re: Partial Evaluations 2
Nice stuff! It reminds me a little of my seminar on cohomology and computation, where I was advocating the bar construction as a systematic way of replacing equations by edges, equations between equations or ‘syzygies’ by triangles, and so on. But I spent the whole seminar explaining the bar construction and didn’t really get very far figuring out the computational aspects. It’s good to see people doing this now. I recommend bringing cohomology into the game.