The n-Category Café

A Petri net is a seemingly simple thing:

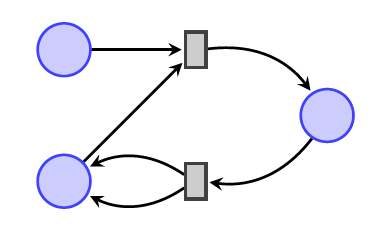
It consists of places (drawn as circles) and transitions (drawn as boxes), with directed edges called arcs from places to transitions and from transitions to places.

The idea is that when you use a Petri net, you put dots called tokens in the places, and then move them around using the transitions:

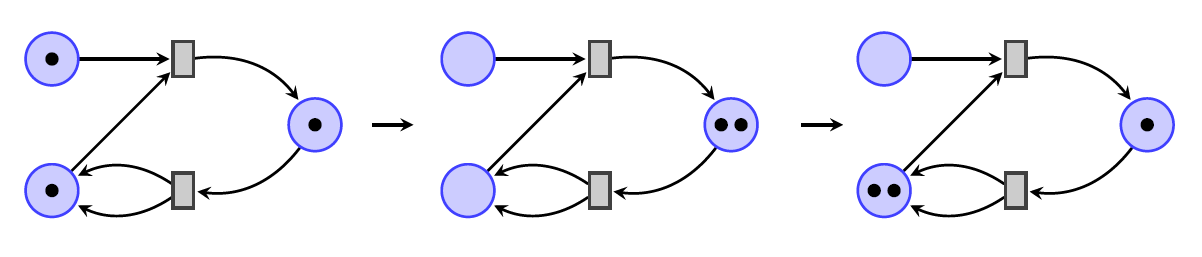
A Petri net is actually a way of describing a monoidal category. A way of putting a bunch of tokens in the places gives an object of this category, and a way of moving them around repeatedly (as above) gives a morphism.

The idea sounds straightforward enough. But it conceals some subtleties, which researchers have been struggling with for at least 30 years.

There are various ways to make the definition of Petri net precise. For example: is there a finite set of arcs from a given place to a given transition (and the other way around), or merely a natural number of arcs? If there is a finite set, is this set equipped with an ordering or not? Furthermore, what is a morphism between Petri nets?

Different answers are good for different purposes. In the so-called ‘individual token philosophy’, we allow a finite set of tokens in each place. In the ‘collective token philosophy’, we merely allow a natural number of tokens in each place. It’s like the difference between having 4 individual workers named John, Fabrizio, Jade and Mike where you can tell who did what, and having 4 anonymous workers: nameless drones.

Our goal was to sort this out all and make it crystal clear. We focus on 3 kinds of net, each of which naturally generates its own kind of monoidal category:

• pre-nets, which generate free strict monoidal categories.
• Σ-nets, which generate free symmetric strict monoidal categories.
• Petri nets, which generate free commutative monoidal categories.

These three kinds of monoidal category differ in how ‘commutative’ they are:

• In a strict monoidal category we typically have $x \otimes y \ne y \otimes x$.

• In a strict symmetric monoidal category we have for each pair of objects a chosen isomorphism $x \otimes y \cong y \otimes x$.

• A commutative monoidal category is a symmetric strict monoidal category where the symmetry isomorphisms are all identities, so $x \otimes y = y \otimes x$.

So, we have a spectrum running from hardcore individualism, where two different things of the same type are never interchangeable… to hardcore collectivism, where two different things of the same type are so interchangeable that switching them counts as doing nothing at all! In the theory of Petri nets and their variants, the two extremes have been studied better than the middle.

You can summarize the story with this diagram:

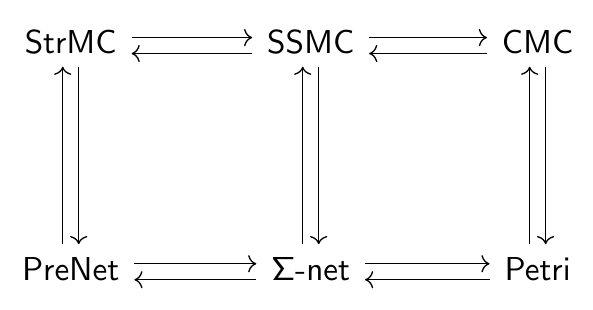
There are three different categories of nets at bottom, and three diffferent categories of monoidal categories on top — all related by adjoint functors! Here the left adjoints point up the page — since different kinds of nets freely generate different kinds of monoidal categories — and also to the right, in the direction of increasing ‘commutativity’.

If you’re a category theorist you’ll recognize at least two of the three categories on top:

• $\mathsf{StrMC}$, with strict monoidal categories as objects and strict monoidal functors as morphisms.

• $\mathsf{SSMC}$, with symmetric strict monoidal categories as objects and strict symmetric monoidal functors as their morphisms.

• $\mathsf{CMC}$, with commutative monoidal categories as objects and strict symmetric monoidal functors as morphisms. A commutative monoidal category is a symmetric strict monoidal category where the symmetry is the identity.

The categories of nets are probably less familiar. But they are simple enough. Here I’ll just describe their objects. The morphisms are fairly obvious, but read our paper for details.

• $\mathsf{PreNet}$, with pre-nets as objects. A pre-net consists of a set $S$ of places, a set $T$ of transitions, and a function $T \to S^\ast\times S^\ast$, where $S^\ast$ is the underlying set of the free monoid on $S$.

• Σ$\mathsf{-net}$, with Σ-nets as objects. A Σ-net consists of a set $S$, a groupoid $T$, and a discrete opfibration $T \to P S \times P S^{\mathrm{op}}$, where $P S$ is the free symmetric strict monoidal category generated by a set of objects $S$ and no generating morphisms.

• $\mathsf{Petri}$, with Petri nets as objects. A Petri net, as we use the term, consists of a set $S$, a set $T$, and a function $T \to \mathbb{N}[S] \times \mathbb{N}[S]$, where $\mathbb{N}[S]$ is the underlying set of the free commutative monoid on $S$.

What does this mean in practice?

• In a pre-net, each transition has an ordered list of places as ‘inputs’ and an ordered list of places as ‘outputs’. We cannot permute the inputs or outputs of a transition.

• In a Σ-net, each transition has an ordered list of places as inputs and an ordered list of places as outputs. However, permuting the entries of these lists gives a new transition with a new list of inputs and a new list of outputs!

• In a Petri net, each transition has a multiset of places as inputs and a multiset of places as outputs. A multiset is like an ‘unordered list’: entries can appear repeatedly, but the order makes no difference at all.

So, pre-nets are rigidly individualist. Petri nets are rigidly collectivist. And Σ-nets are flexible, including both extremes as special cases!

On the one hand, we can use the left adjoint functor

$$\mathsf{PreNet} \to \Sigma\mathsf{-net}$$

to freely generate Σ-nets from pre-nets. If we do this, we get Σ-nets such that permutations of inputs and outputs act freely on transitions. Joachim Kock has recently studied Σ-nets of this sort. He calls them whole-grain Petri nets, and he treats them as forming a category in their own right, but it’s also the full image of the above functor.

On the other hand, we can use the right adjoint functor

$$\mathsf{Petri} \to Σ\mathsf{-net}$$

to turn Petri nets into Σ-nets. If we do this, we get Σ-nets such that permutations of inputs and outputs act trivially on transitions: the permutations have no effect at all.

I’m not going to explain how we got any of the adjunctions in this diagram:

That’s where the interesting category theory comes in. Nor will I tell you about the various alternative mathematical viewpoints on Σ-nets… nor how we draw them. I also won’t explain our work on open nets and open categories of all the various kinds. I’m hoping Mike Shulman will say some more about what we’ve done. That’s why this blog article is optimistically titled “Part 1”.

But I hope you see the main point. There are three different kinds of things like Petri nets, each of which serves to freely generate a different kind of monoidal category. They’re all interesting, and a lot of confusion can be avoided if we don’t mix them up!