Native Type Theory (Part 2)
Posted by John Baez
guest post by Christian Williams
We’re continuing the story of Native Type Theory.
In Part 1 we introduced the internal language of a topos. Now, we describe the kinds of categories from which we will construct native type systems, via the internal language of the presheaf topos .
We can represent a broad class of languages as categories with products and exponents. The idea of native type theory is simply that for any such language , we can understand the internal language of as the language of expanded by predicate logic and dependent type theory.
.png)
The type system reasons about abstract syntax trees, the trees of constructors which form terms:
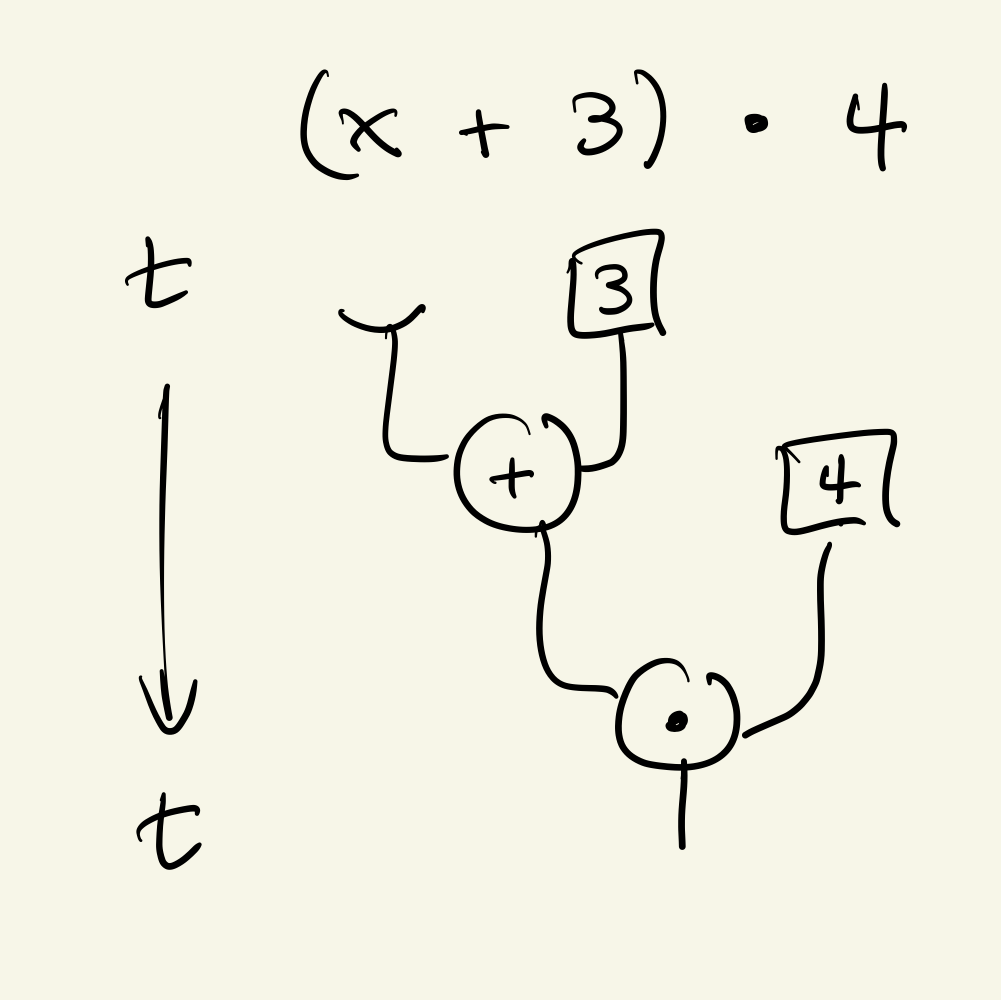
The types of native type theory are basically indexed sets of these operations, built from and constructors of . For example, given the “theory of a monoid” with operations and , we can construct the predicate:
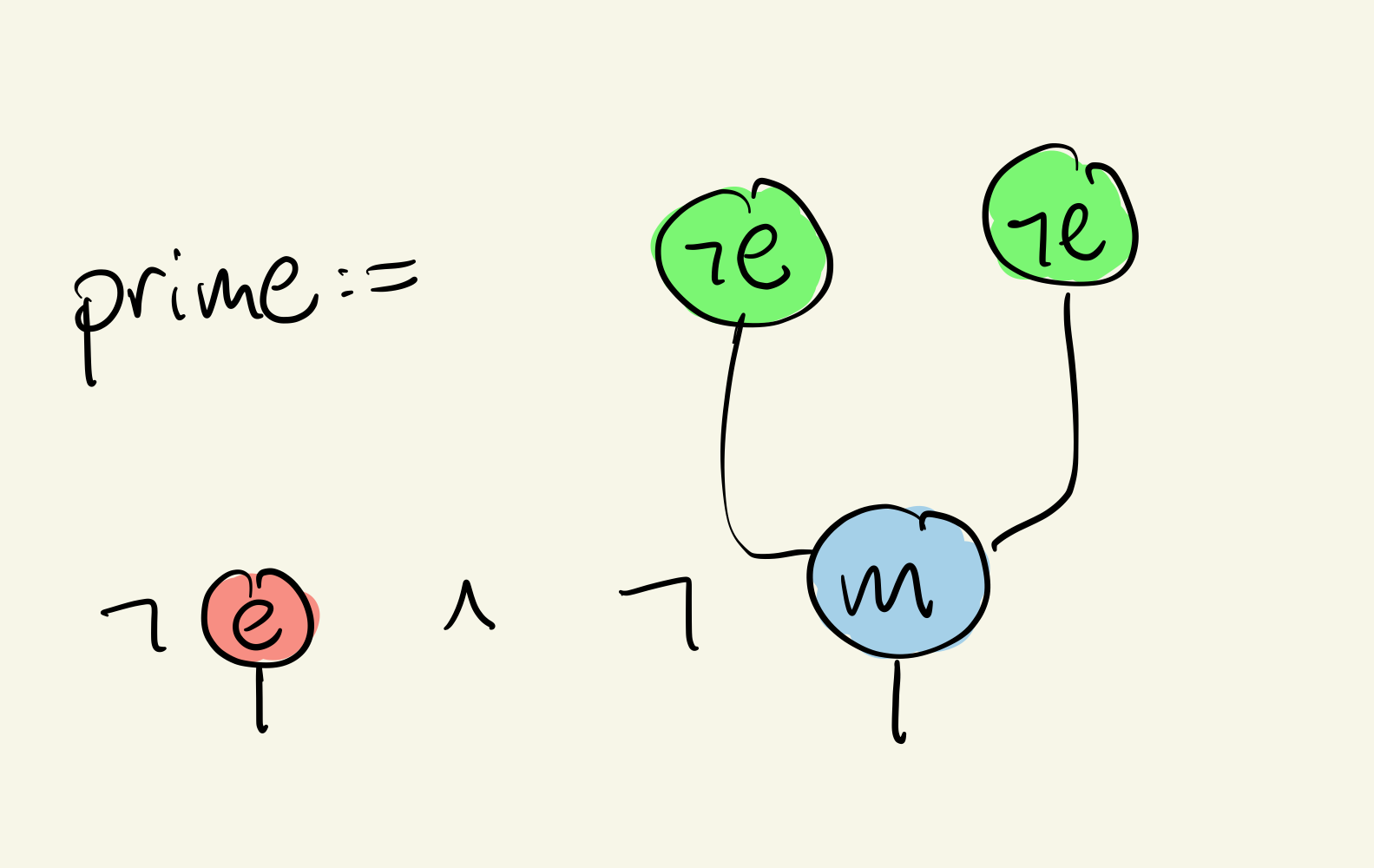
(shorthand for formal notation in the presheaf topos.) This corresponds to the subset of terms which are not the unit and not the product of two nonunits. In a concurrent language where multiplication is parallel execution, this is the predicate for “single-threaded” processes.
By including a graph of rewrites and terms , we can also reason not only about term structure but also behavior. Using logic on this graph, one can reconstruct modalities, bisimulation, and more. For example, given the type “single-threaded” we can take preimage along to get rewrites whose target is in that type, and then take image along to get their source. Then is “terms which rewrite to be single-threaded”. One can express “terms which always satisfy a security condition ”.
Though native types are built from the constructors of the original language, they naturally expand the language with logic and type theory, to give a sound and complete system for reasoning about the structure and behavior of terms.
First we describe the class of categories which represent our basic languages.
Higher-order algebraic theories
Many structures can be represented abstractly as categories with finite products or limits, and then modelled by a functor, e.g. a ring object in sheaves. In logic and computer science (and mathematics), there are higher-order operations whose operands are themselves operations, such as universal quantification with predicates and -abstraction with expressions.

The concept of Higher-order algebraic theory has recently been defined by Arkor and McDermott. A higher-order algebraic theory of sort and order is a cartesian category with exponents up to order , freely generated from a set of objects and a presentation of operations and equations.
An operation is a rule which inputs terms of the form and outputs a term of sort . Higher-order operations bind the variables of their operands, which enables the definition of substitution. Our main example is the input operation in a concurrent language, which is essentially a -abstraction “located at a channel” (see -calculus below).
In the nexus of category theory, computer science, and logic, the idea of representing binding operations using exponents is well-known. But this model does not tell us how to actually implement these operations, i.e. it does not tell us how to implement capture-avoiding substitution. There is a model which does, using the “substitution monoidal structure” on , as given by Fiore, Plotkin, & Turi. Fortunately this was proven equivalent to exponential structure by Fiore & Mahmoud.
Higher-order algebraic theories extend multisorted algebraic theories with binding operations. Because the concept is parameterized by order, the tower of -theories provides a bridge all the way from cartesian categories to cartesian closed categories. Best of all, order- theories correspond to monads on order- theories: this justifies the idea that “higher-order operations are those whose operands are operations”. So, the theory-monad correspondence extends to incorporate binding.
An order- theory defines a monad on order- theories by a formula which generalizes the one for Lawvere theories:
where is the free cartesian category with exponents up to order on the set of sorts , and is the free -theory on the -theory .
We now proceed with our main example of a language given by a higher-order algebraic theory.
-calculus
RChain is a distributed computing system based on the -calculus, a concurrent language in which a program is not a sequence of instructions but a multiset of parallel processes. Each process is opting to send or receive information along a channel or “name”, and when they sync up on a name they can “communicate” and transfer information. So computation is interactive, providing a unified language for both computers and networks.
The classic concurrent language is the -calculus. Its basic rule is communication:
The -calculus adds reflection: operators which turn processes (code) into names (data) and vice versa. Names are not atomic symbols; they are references to processes. Code can be sent as a message, then evaluated in another context — this “code mobility” allows for deep self-reference.
We can model the -calculus as a second-order theory with sorts for processes and for names. These act as code and data respectively, and the operations of reference and dereference transform one into the other. There is a third sort for rewrites. Terms are built up from one constant, the null process 0. The two basic actions of a process are output and input , and parallel gives binary interaction: these get their meaning in the communication rule.
We present the operations, equations, and rewrites of the -calculus.
The basic operations:
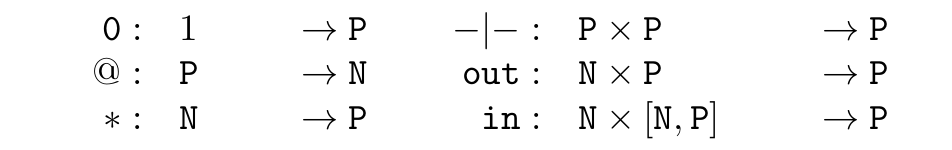
The rewrites (bottom two allow a rewrite to occur inside a parallel):
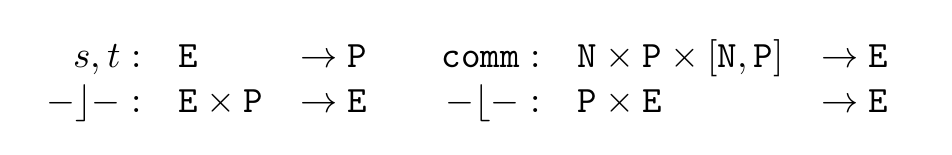
The main rule, communication, plus the basic equations:
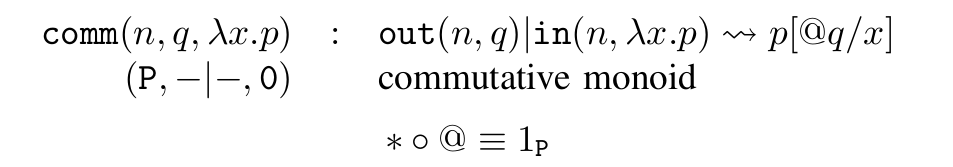
The rules that make rewrites-inside-parallels make sense:
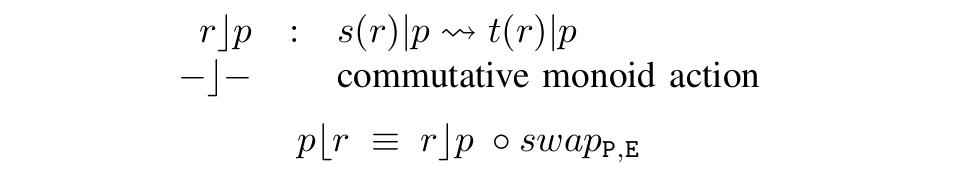
(here is shorthand for and .)
As an example, we can construct recursive processes using reflection, without any special operator. On a given name , we can define a context which replicates processes as follows.
Then when you plug in a process , one can check that . This magical operation acts as a “replicating machine” which duplicates a process, executing one copy and passing the other back as a message.
The -calculus serves as the main running example in our paper, as concurrency allows for reasoning about networks (such as security), and reflection enables the type system to reason about both code and data, and explore connections between the two basic notions of computation.
In Part 3 we present the native type system of the -calculus, the internal language of the presheaf topos on , and demonstrate applications. Thank you for reading, and let me know your thoughts.

Re: Native Type Theory (Part 2)
Let me ask the same question I always do when I talk to you about this, which is why we care about order- theories for ?
A first-order algebraic theory is an ordinary algebraic theory, whose semantic incarnation is a category with finite products. An -order algebraic theory is an ordinary -calculus, whose semantic incarnation is a cartesian closed category. What’s the value in stratifying things further?
I can sort of see the motivation for second-order algebraic theories, in which only a specified set of generating objects are exponentiable. They seem like sort of a simply-typed counterpart of the representable map categories introduced by Taichi Uemura for describing type theories, in which only a restricted class of judgments can be “hypothesized”. On the other hand, Gratzer and Sterling have recently shown that locally cartesian closed categories are conservative over representable map categories, so no expressivity is lost in the dependently typed case by just using LCCCs. It seems likely that something similar would be true in the simply typed case.
Are there important examples of th order algebraic theories for ? Is there something concrete we gain by allowing ?