The n-Category Café

You may wonder why I’m returning to this now, after three months of silence. The reason is that Kenny, Christina Vasilakopolou, and I just finished a paper that continues this story:

• John Baez, Kenny Courser and Christina Vasilakopoulou, Structured versus decorated cospans.

We showed that under certain conditions, structured and decorated cospans are equivalent. So, I’m excited about this stuff again.

Last time I explained Fong’s theorem about decorated cospans:

Fong’s Theorem. Suppose $\mathsf{A}$ is a category with finite colimits, and make $\mathsf{A}$ into a symmetric monoidal category with its coproduct as the tensor product. Suppose $F\colon (\mathsf{A},+) \to (\mathsf{Set},\times)$ is a symmetric lax monoidal functor. Define an F-decorated cospan to be a cospan

       

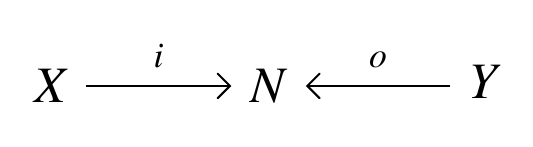
in $\mathsf{A}$ together with an element $x\in F(N)$ called a decoration. Then there is a symmetric monoidal category with

• objects of $\mathsf{A}$ as objects,
• isomorphism classes of $F$-decorated cospans as morphisms.

The theorem is true, but it doesn’t apply to all the examples we wanted it to. The problem is that it’s ‘not categorified enough’. It’s fine if we want to decorate the apex $N$ of our cospan with some extra structure: we do this by choosing an element of some set $F(N).$ But in practice, we often want to decorate $N$ with some extra stuff, which means choosing an object of a category $F(N).$ So we should really use not a functor

$$F\colon (\mathsf{A},+) \to (\mathsf{Set},\times)$$

but something like a functor

$$F\colon (\mathsf{A},+) \to (\mathbf{Cat},\times)$$

What do I mean by ‘something like a functor?’ Well, $\mathbf{Cat}$ is not just a category but a 2-category: it has categories as objects, functors as morphisms, but also natural transformations as 2-morphisms. The natural notion of ‘something like a functor’ from a category to a 2-category is called a pseudofunctor. And just as we can define symmetric lax monoidal functor, we can define a symmetric lax monoidal pseudofunctor.

All these nuances really matter when we’re studying open graphs, as we were last time!

Here we want the feet of our structured cospan to be finite sets and the apex to be a finite graph. So, we have $\mathsf{A} = \mathsf{FinSet}$ and for any $N \in \mathsf{FinSet}$ we want $F(N)$ to be the set, or category, of finite graphs having $N$ as their set of nodes.

I explained last time all the disasters that ensue when you try to let $F(N)$ be the set of finite graphs having $N$ as its set of nodes. You can try, but you will pay dearly for it! You can struggle and fight, like Hercules trying to chop all the heads off the Hydra, but you still can’t get a symmetric lax monoidal functor

$$F\colon (\mathsf{A},+) \to (\mathsf{Set},\times)$$

that sends any finite set $N$ to the set of graphs having $N$ as their set of nodes.

But there is a perfectly nice category $F(N)$ of all finite graphs having $N$ as their set of nodes. And you can get a symmetric lax monoidal pseudofunctor

$$F\colon (\mathsf{A},+) \to (\mathbf{Cat},\times)$$

that sends any any finite set to the category of finite graphs having it as nodes. So you should stop fighting and go with the flow.

Kenny, Christina and I proved an enhanced version of Fong’s theorem that works starting from this more general kind of $F.$ And instead of just giving you a symmetric monoidal category, this theorem gives you a symmetric monoidal double category.

In fact, that is something you should have wanted already, even with Fong’s original hypotheses! The clue is that Fong’s theorem uses isomorphism classes of decorated cospans, which suggests we’d get something better if we used decorated cospans themselves. Kenny tackled this a while ago, getting a version of Fong’s theorem that produces a symmetric monoidal double category, and another version that produces a symmetric monoidal bicategory:

• Kenny Courser, A bicategory of decorated cospans, Theory and Applications of Categories 32 (2017), 995–1027.

Over the years we’ve realized that the double category is better, because it contains more information and is easier to work with. So, in our new improved approach to decorated cospans, we go straight for the jugular and get a double category. And here’s how it works:

Theorem. Suppose $\mathsf{A}$ is a category with finite colimits, and make $\mathsf{A}$ into a symmetric monoidal category with its coproduct as the tensor product. Suppose $F\colon (\mathsf{A},+) \to (\mathbf{Cat},\times)$ is a symmetric lax monoidal pseudofunctor. Then there is a symmetric monoidal double category $F\mathbb{C}\!\mathbf{sp}$ in which

• an object is an object of $\mathsf{A}$
• a vertical morphism is a morphism in $\mathsf{A}$
• a horizontal morphism is an F-decorated cospan, meaning a cospan in $\mathsf{A}$ together with a decoration:

             

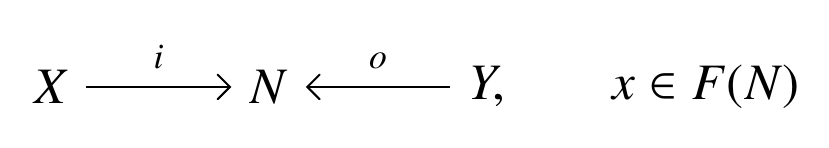
• a 2-morphism is a map of decorated cospans, meaning a commutative diagram in $\mathsf{A}$:

             

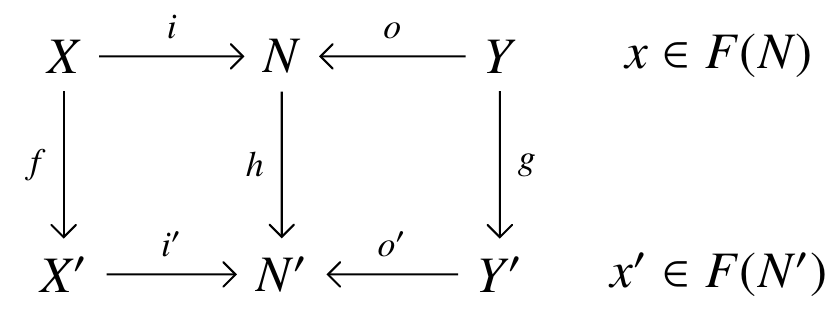
together with a morphism $\tau \colon F(h)(x) \to x',$ the map of decorations.

We call $F\mathbb{C}\!\mathbf{sp}$ a decorated cospan double category. And as our paper explains, this idea lets us fix all the broken attempted applications of Fong’s original decorated cospan categories!

All this is just what any category theorist worth their salt would try, in order to fix the original problems with decorated cospans. It turns out that proving the theorem above is not so easy, mainly because the definition of ‘symmetric monoidal double category’ is rather complex. But if you accept the theorem—including the details of how you get the symmetric monoidal structure on the double category, which I have spared you here—then it doesn’t really matter much that the proof takes work.

Next time I’ll tell you about the other way to fix the original decorated cospan formalism: structured cospans. When these work, they are often easier to use.

---

• Part 1: an overview of Courser’s thesis and related papers.

• Part 2: problems with the original decorated cospans.

• Part 3: the new improved decorated cospans.