Open Systems: A Double Categorical Perspective (Part 1)
Posted by John Baez
Kenny Courser’s thesis has hit the arXiv:
- Kenny Courser, Open Systems: A Double Categorical Perspective, Ph.D. thesis, U. C. Riverside, 2020.
He’s been the driving force behind a lot of work on open systems and networks at U. C. Riverside. By the way, he’s looking for a job, so if you think you know a position that’s good for someone who can teach all kinds of math and also strong on applied category theory, give him or me a shout.
But let me describe his thesis.
His thesis is big! It lays out a general approach to open systems—systems that can interact with their environment. In this approach, you can attach open systems in series to form larger open systems, so they act like morphisms in a category:
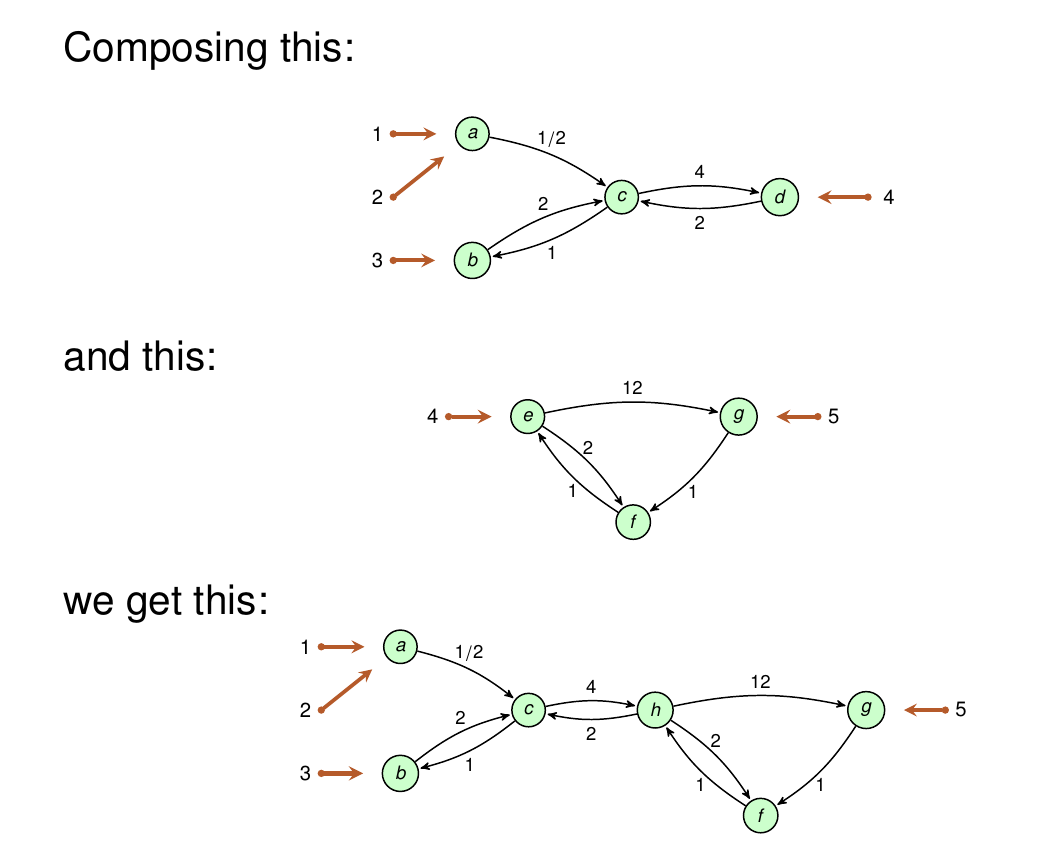
But you can also study 2-morphisms between open systems. These describe ways to include a little system in a bigger one, or simplify a big complicated system down to smaller one:
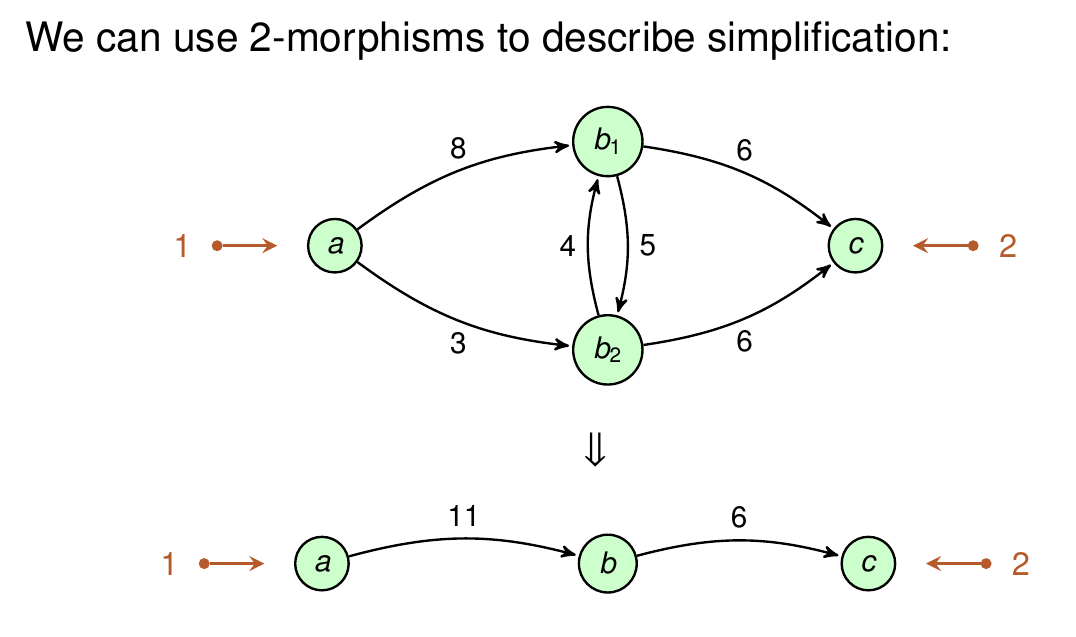
To handle all this, Courser uses double categories, which he explains.
His formalism also lets you set two open systems side by side ‘in parallel’ and get a new open system:
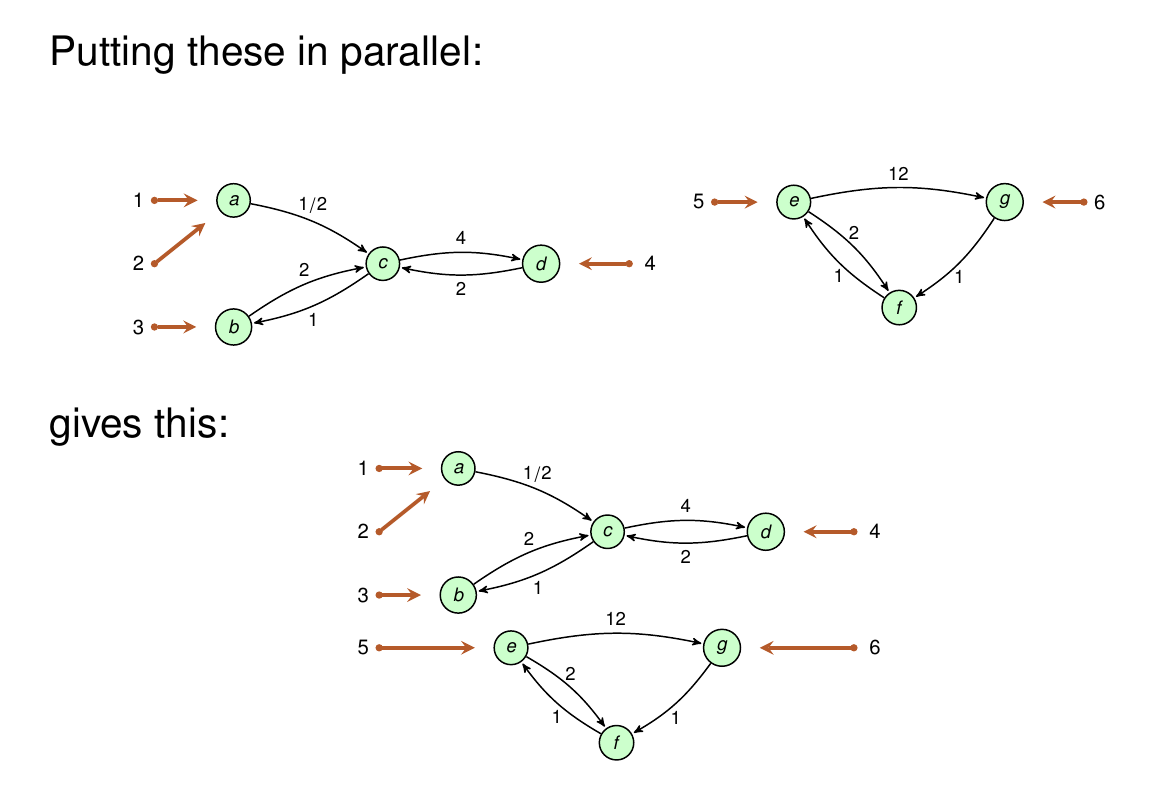
To handle this, he uses symmetric monoidal double categories. He explains what these are, and how to get them. And he illustrates his setup with examples:
At a more technical level, Courser explains the problems with Brendan Fong’s and my work on decorated cospans and shows how to fix in not just one but two ways: using structured cospans, and using a new improved version of decorated cospans. He also shows that these two approaches are equivalent under fairly general conditions.
His thesis unifies a number of papers:
Kenny Courser, A bicategory of decorated cospans, Theory and Applications of Categories 32 (2017), 995–1027.
John Baez and Kenny Courser, Coarse-graining open Markov processes, Theory and Applications of Categories 33 (2018), 1223–1268. (Blog article here.)
John Baez and Kenny Courser, Structured cospans. (Blog article here.)
John Baez, Kenny Courser and Christina Vasilakopoulou, Structured versus decorated cospans.
The last introduces the new improved decorated cospans and proves their equivalence to structured cospans under some conditions.
I think next time I’ll explain the problems with the original decorated cospan formalism. Another nice thing about Kenny’s thesis is that it goes over a bunch of papers that were afflicted by these problems, and it shows how to fix them.

Re: Open Systems: A Double Categorical Perspective (Part 1)
So if structured cospans are equivalent to improved decorated cospans, which one should we be using from now on? Are the “fairly general conditions” for this equivalence general enough that it makes no difference? Or are there important examples falling outside these general conditions?