Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

October 21, 2020

Epidemiological Modeling With Structured Cospans

Posted by John Baez

This is a wonderful development! Micah Halter and Evan Patterson have taken my work on structured cospans with Kenny Courser and open Petri nets with Jade Master, together with Joachim Kock’s whole-grain Petri nets, and turned them into a practical software tool!

Then they used that to build a tool for ‘compositional’ modeling of the spread of infectious disease. By ‘compositional’, I mean that they make it easy to build more complex models by sticking together smaller, simpler models.

Even better, they’ve illustrated the use of this tool by rebuilding part of the model that the UK has been using to make policy decisions about COVID19.

All this software was written in the programming language Julia.

I had expected structured cospans to be useful in programming and modeling, but I didn’t expect it to happen so fast!

For details, read this great article:

Abstract. The field of applied category theory (ACT) aims to put the compositionality inherent to scientific and engineering processes on a firm mathematical footing. In this post, we show how the mathematics of ACT can be operationalized to build complex epidemiological models in a compositional way. In the first two sections, we review the idea of structured cospans, a formalism for turning closed systems into open ones, and we illustrate its use in Catlab through the simple example of open graphs. Finally, we put this machinery to work in the setting of Petri nets and epidemiological models. We construct a portion of the COEXIST model for the COVID-19 pandemic and we simulate the resulting ODEs.

You can also see related articles by James Fairbanks, Owen Lynch and Evan Patterson here:

Also try these videos:

I’m biased, but I think this is really cool cutting-edge stuff. If you want to do work along these lines let me know here and I’ll get Patterson to take a look.

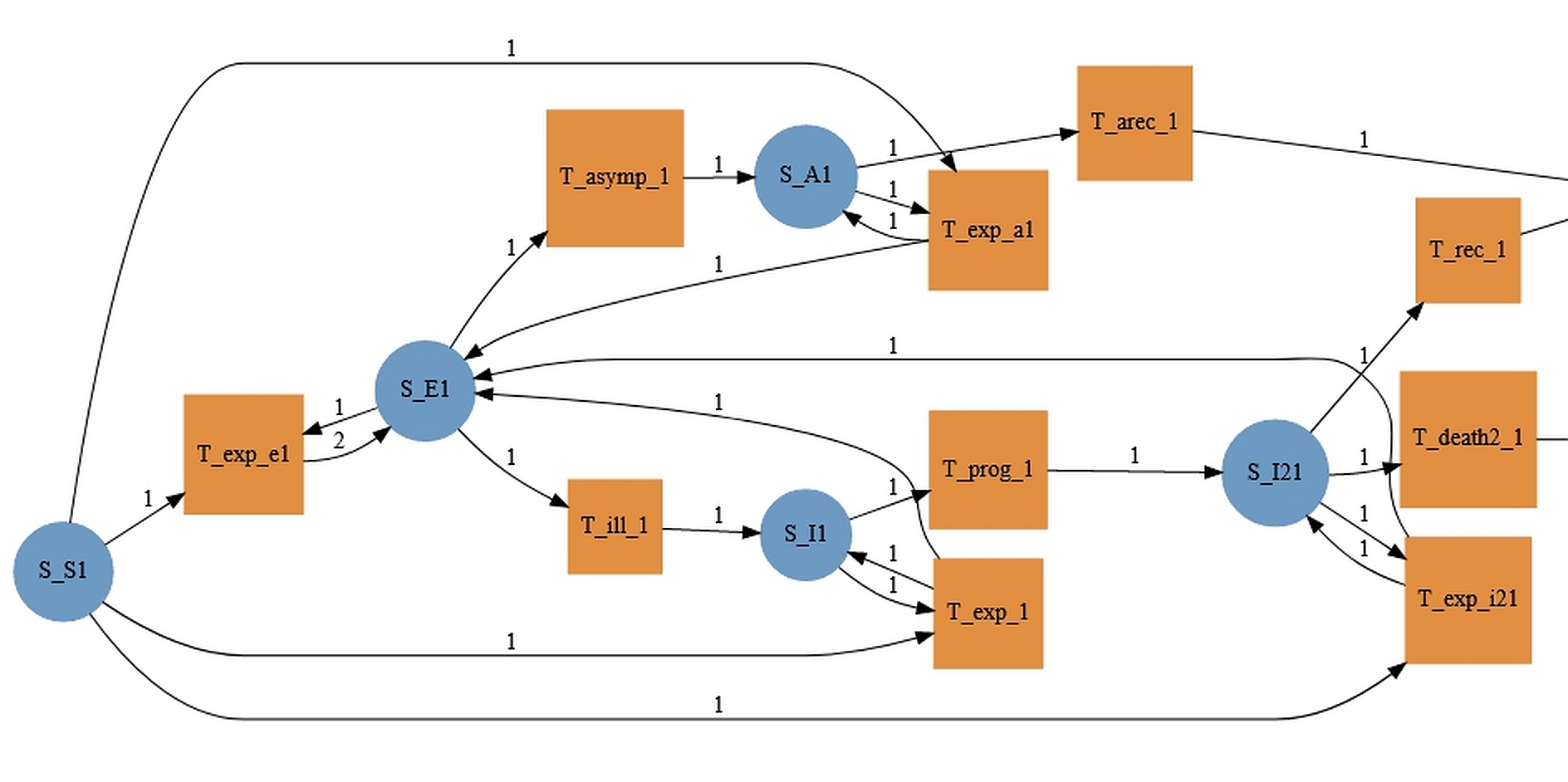
Here’s part of a network created using their software:

Posted at October 21, 2020 9:14 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3259



4 Comments & 0 Trackbacks

Jeffery

Here is a talk where they apply topology to studying COVID-19, the evolution of the virus, and the current pandemic.

https://www.youtube.com/watch?v=PUXYLsaNdQg&feature=youtu.be

Posted by: Jeffery Winkler on October 21, 2020 11:32 PM | Permalink | Reply to this

Re: Epidemiological Modeling With Structured Cospans

Forgive my ignorance - I don’t (yet) know anything about Julia or Structured Cospans, but I know just a tiny bit about monoidal categories.

I’m very interested in understanding how we go from this graph network to actual ODE’s. Glancing through related articles about structured cospans and Petri nets nothing really jumps out to me - perhaps its hidden within a formalism I don’t know about.

Can someone give me some pointers on what to read to understand the mathematics of [Network -> System of ODE’s] (even just where the relevant definitions are located)?

I’m a PhD student and currently studying Stochastic Modified Equations which is a formalism one can use to analyze the behavior of learning algorithms such as Stochastic Gradient Descent.

I have this extremely vague idea that if I ever make the step from very simple (say quadratic) error functions (not to be confused with loss functions) to error functions coming from a Deep Neural Networks, a compositional approach, relating the layers to a sort of “composition” or network of coupled SDE’s, will become very valuable - so I’m interested in any formalism where we compose and tensor Differential Equations.

Posted by: Stefan Perko on October 25, 2020 2:14 PM | Permalink | Reply to this

Re: Epidemiological Modeling With Structured Cospans

Stefan wrote:

Can someone give me some pointers on what to read to understand the mathematics of [Network -> System of ODE’s] (even just where the relevant definitions are located)?

The relevant buzzword is ‘rate equation of a stochastic Petri net’, and you can learn about this starting in Chapter 1 of my free book:

Don’t worry, you don’t need to know anything about quantum physics or stochastic anything to understand this chapter!

For more details on how open stochastic Petri nets get turned into systems of ODEs, try this:

Here instead of ‘stochastic Petri net’ we often say ‘reaction network with rates’—but they’re almost the same thing so the difference doesn’t really matter, as we explain.

I should warn you that Patterson and Halter use a somewhat different formalism to describe stochastic Petri nets… but the difference is so subtle that it only matters when you get really serious about this stuff.

I’m interested in any formalism where we compose and tensor differential equations.

That’s what Blake and I are talking about in our paper. Take a look at our category Dynam. We get a functor from the category of ‘open reaction networks with rates’ to Dynam, that turns any reaction network with rates into a bunch of coupled nonlinear ordinary differential equations. Once you get how this goes, it should be easy—or at least possible—to cook up variants of this idea suitable for whatever you’re interested in.

You might also like my talk on this stuff.

Posted by: John Baez on October 25, 2020 9:06 PM | Permalink | Reply to this

Re: Epidemiological Modeling With Structured Cospans

Many thanks!

I now know about rate equations and your paper seems to go into the monoidal cat. direction I was hoping for, with DE’s. Good stuff!

Posted by: Stefan Perko on October 27, 2020 9:55 AM | Permalink | Reply to this

Post a New Comment