Sets of Sets of Sets of Sets of Sets of Sets
Posted by John Baez
The covariant power set functor can be made into a monad whose multiplication turns a subset of the set of subsets of into a subset of by taking their union. Algebras of this monad are complete semilattices.
But what about powers of the power set functor? Yesterday Jules Hedges pointed out this paper:
- Bartek Klin and Julian Salamanca, Iterated covariant powerset is not a monad.
The authors prove that cannot be made into a monad for .
I’ve mainly looked at their proof for the case . I haven’t completely worked through it, but it focuses on the unit of any purported monad structure for , rather than its multiplication. Using a cute Yoneda trick they show there are only four possible units, corresponding to the four elements of . Then they show these can’t work. The argument involves sets like this:
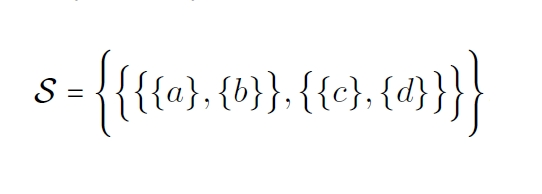
As far as I’ve seen, they don’t address the following question:
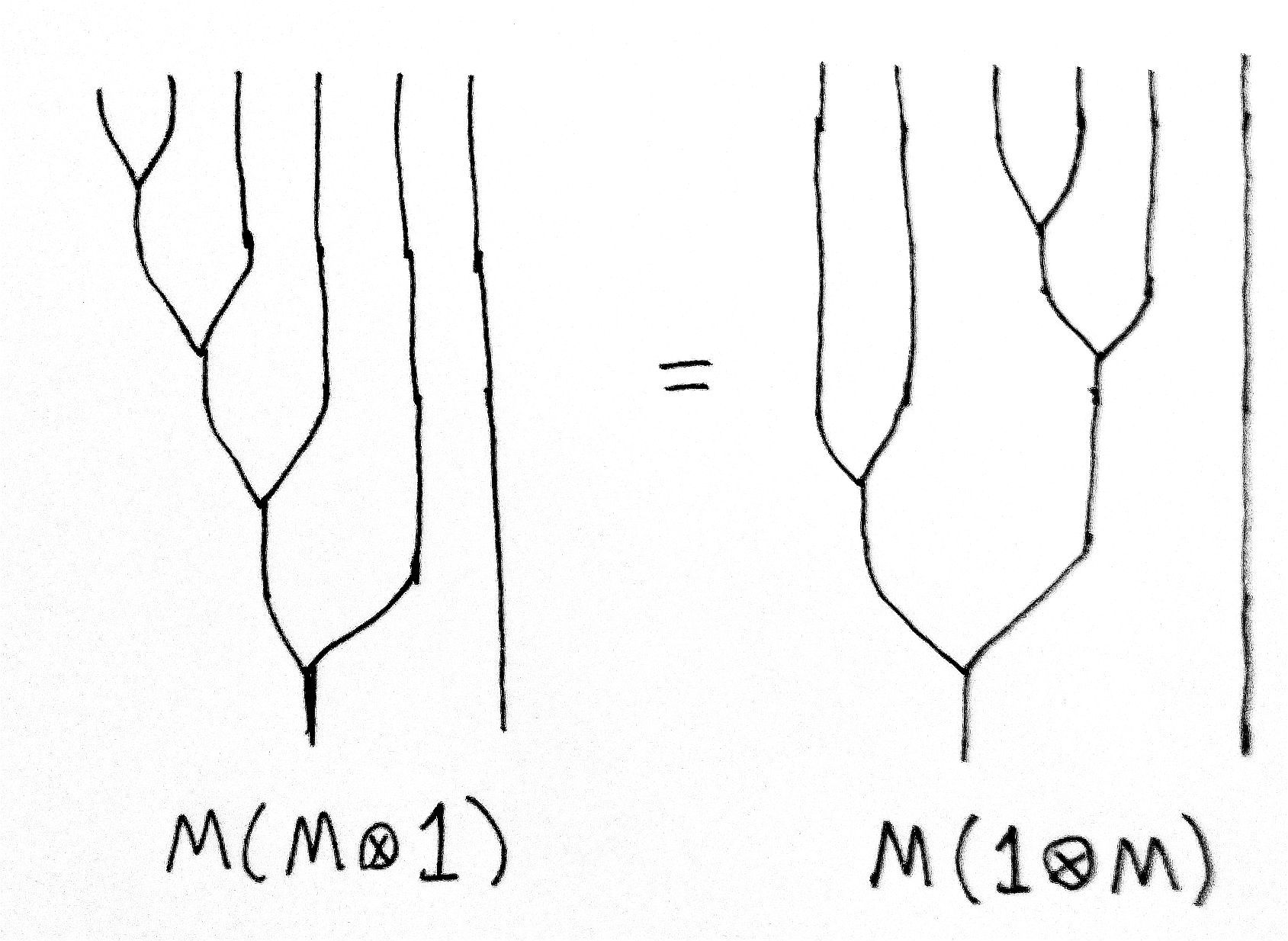
Question. Does there exist an associative multiplication ? In other words, is there a natural transformation such that
equals
I’m not very good at these things, so this question might be very easy to answer. But if the answer were “obviously no” then you’d think Klin and Salamanca might have mentioned that. They do prove there is no distributive law . But they also give examples of monads for which there’s no distributive law , yet there’s still a way to make into a monad.
As far as I can tell, my question is fairly useless: does anyone consider “semigroupads”, namely monads without unit? Nonetheless I’m curious.
If there were a positive answer, we’d have a natural way to take a set of sets of sets of sets and turn it into a set of sets in such a way that the two most obvious resulting ways to turn a set of sets of sets of sets of sets of sets into a set of sets agree!

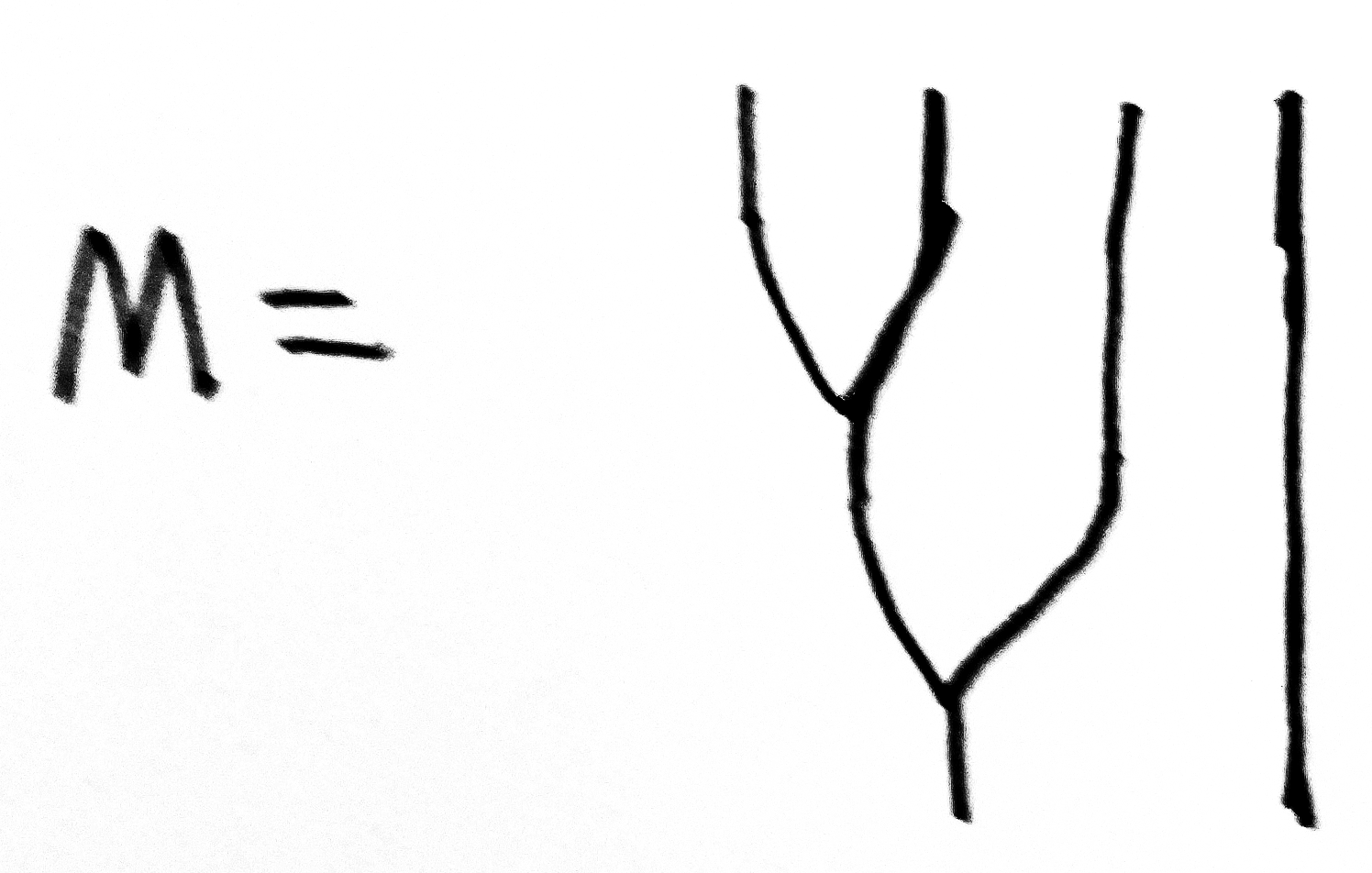
Re: Sets of Sets of Sets of Sets of Sets of Sets
It comes up occasionally in Haskell.