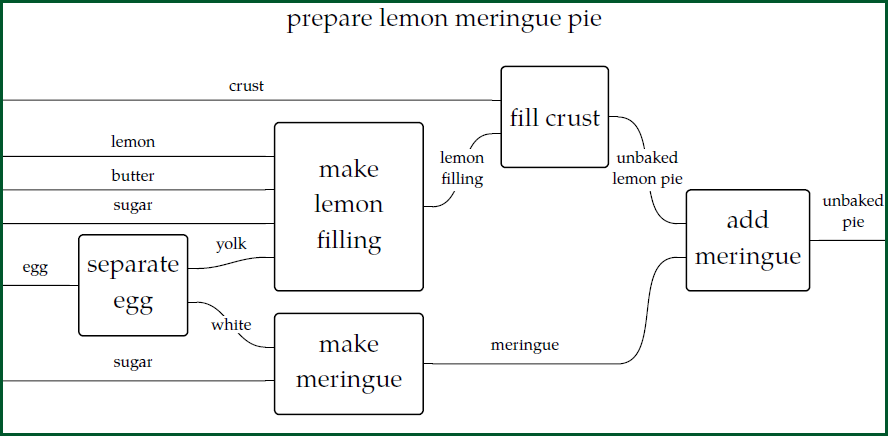
Applied Category Theory: Resource Theories
Posted by John Baez
My course on applied category theory is continuing! After a two-week break where the students did exercises, I went back to lecturing about Fong and Spivak’s book Seven Sketches. The second chapter is about ‘resource theories’.
Resource theories help us answer questions like this:
- Given what I have, is it possible to get what I want?
- Given what I have, how much will it cost to get what I want?
- Given what I have, how long will it take to get what I want?
- Given what I have, what is the set of ways to get what I want?
Resource theories in their modern form were arguably born in these papers:
Bob Coecke, Tobias Fritz and Robert W. Spekkens, A mathematical theory of resources.
Tobias Fritz, Resource convertibility and ordered commutative monoids.
We are lucky to have Tobias in our course, helping the discussions along! He’s already posted some articles on resource theory on the Azimuth blog:
Tobias Fritz, Resource convertibility (part 1), Azimuth, 7 April 2015.
Tobias Fritz, Resource convertibility (part 2), Azimuth, 10 April 2015.
Tobias Fritz, Resource convertibility (part 3), Azimuth, 13 April 2015.
In the course, we had fun bouncing between the relatively abstract world of monoidal preorders and their very concrete real-world applications to chemistry, scheduling, manufacturing and other topics. Here are the lectures:
- Lecture 18 - Chapter 2: Resource Theories
- Lecture 19 - Chapter 2: Chemistry and Scheduling
- Lecture 20 - Chapter 2: Manufacturing
- Lecture 21 - Chapter 2: Monoidal Preorders
- Lecture 22 - Chapter 2: Symmetric Monoidal Preorders
- Lecture 23 - Chapter 2: Commutative Monoidal Posets
- Lecture 24 - Chapter 2: Pricing Resources
- Lecture 25 - Chapter 2: Reaction Networks
- Lecture 26 - Chapter 2: Monoidal Monotones
- Lecture 27 - Chapter 2: Adjoints of Monoidal Monotones
- Lecture 28 - Chapter 2: Ignoring Externalities
- Lecture 29 - Chapter 2: Enriched Categories
- Lecture 30 - Chapter 2: Preorders as Enriched Categories
- Lecture 31 - Chapter 2: Lawvere Metric Spaces
- Lecture 32 - Chapter 2: Enriched Functors
- Lecture 33 - Chapter 2: Tying Up Loose Ends