Props in Network Theory
Posted by John Baez
Long before the invention of Feynman diagrams, engineers were using similar diagrams to reason about electrical circuits and more general networks containing mechanical, hydraulic, thermodynamic and chemical components. We can formalize this reasoning using ‘props’: that is, strict symmetric monoidal categories where the objects are natural numbers, with the tensor product of objects given by addition. In this approach, each kind of network corresponds to a prop, and each network of this kind is a morphism in that prop. A network with inputs and outputs is a morphism from to Putting networks together in series is composition, and setting them side by side is tensoring.
In this paper, we study the props for various kinds of electrical circuits:
- John Baez, Brandon Coya and Franciscus Rebro, Props in network theory.
We start with circuits made solely of ideal perfectly conductive wires. Then we consider circuits with passive linear components like resistors, capacitors and inductors. Finally we turn on the power and consider circuits that also have voltage and current sources.
And here’s the cool part: each kind of circuit corresponds to a prop that pure mathematicians would eventually invent on their own! So, what’s good for engineers is often mathematically natural too.
We describe the ‘behavior’ of these various kinds of circuits using morphisms between props. In particular, we give a new proof of the black-boxing theorem proved earlier with Brendan Fong. Unlike the original proof, this new one easily generalizes to circuits with nonlinear components. We also use a morphism of props to clarify the relation between circuit diagrams and the signal-flow diagrams in control theory.
Here’s a quick sketch of the main ideas.
In his 1963 thesis, Lawvere introduced functorial semantics: the use of categories with specified extra structure as ‘theories’ whose ‘models’ are structure-preserving functors into other such categories:
- F. W. Lawvere, Functorial semantics of algebraic theories, Ph.D. thesis, Department of Mathematics, Columbia University, 1963. Also in Reprints in Theory and Applications of Categories 5 (2003), 1–121.
In particular, a Lawvere theory is a category with finite cartesian products and a distinguished object such that every object is a power These can serve as theories of mathematical structures that are sets equipped with -ary operations
obeying equational laws. However, structures of a more linear-algebraic nature are often vector spaces equipped with operations of the form
To extend functorial semantics to these, Mac Lane introduced props—or as he called them, ‘PROPs’. The acronym stands for ‘products and permutations’:
- Saunders Mac Lane, Categorical algebra, Bulletin of the American Mathematical Society 71 (1965), 40–106.
A prop is a symmetric monoidal category equipped with a distinguished object such that every object is a tensor power Working with tensor products rather than cartesian products puts operations having multiple outputs on an equal footing with operations having multiple inputs.
Already in 1949 Feynman had introduced his famous diagrams, which he used to describe theories of elementary particles. For a theory with just one type of particle, Feynman’s method amounts to specifying a prop where an operation describes a process with particles coming in and going out. Although Feynman diagrams quickly caught on in physics, only in the 1980s did it become clear that they were a method of depicting morphisms in symmetric monoidal categories. A key step was the work of Joyal and Street, which rigorously justified reasoning in any symmetric monoidal category using ‘string diagrams’—a generalization of Feynman diagrams:
- André Joyal and Ross Street, The geometry of tensor calculus I, Advances in Mathematics 88 (1991), 55–112.
By now, many mathematical physicists are aware of props and the general idea of functorial semantics. In constrast, props seem to be virtually unknown in engineering!
But engineers have been using diagrammatic methods ever since the rise of electrical circuits. And in the 1940s, Olson explained how to apply circuit diagrams to networks of mechanical, hydraulic, thermodynamic and chemical components:
- Harry F. Olson, Dynamical Analogies, Van Nostrand, New York, 1943.
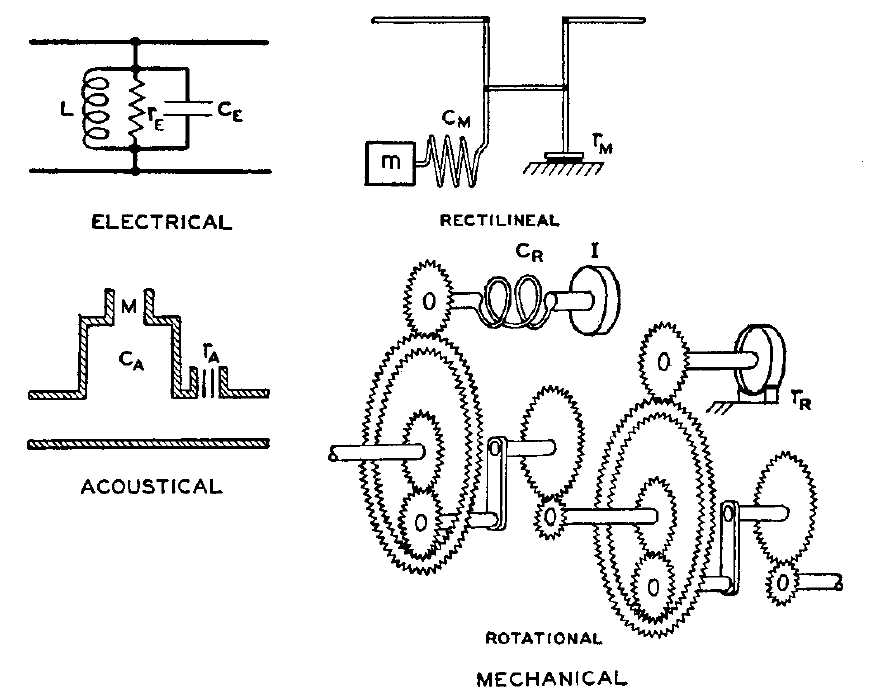
By 1961, Paynter had made the analogies between these various systems mathematically precise using ‘bond graphs’:
- Henry M. Paynter, Analysis and Design of Engineering Systems, MIT Press, Cambridge, Massachusetts, 1961.
Here he shows a picture of a hydroelectric power plant, and the bond graph that abstractly describes it:

By 1963, Forrester was using circuit diagrams in economics:
- Jay Wright Forrester, Industrial Dynamics, MIT Press, Cambridge, Massachusetts, 1961.
In 1984, Odum published a beautiful and influential book on their use in biology and ecology:
- Howard T. Odum, Ecological and General Systems: An Introduction to Systems Ecology, Wiley, New York, 1984.
We can use props to study circuit diagrams of all these kinds! The underlying mathematics is similar in each case, so we focus on just one example: electrical circuits. For other examples, take a look at this:
- John Baez, Network theory (part 29), Azimuth, 23 April 2013.
In our new paper, we illustrate the usefulness of props by giving a new, shorter proof of the ‘black-boxing theorem’ proved here:
- John Baez and Brendan Fong, A compositional framework for passive linear networks. (Blog article here.)
A ‘black box’ is a system with inputs and outputs whose internal mechanisms are unknown or ignored. A simple example is the lock on a doorknob: one can insert a key and try to turn it; it either opens the door or not, and it fulfills this function without us needing to know its inner workings. We can treat a system as a black box through a process called ‘black-boxing’, which forgets its inner workings and records only the relation it imposes between its inputs and outputs. Systems with inputs and outputs can be seen as morphisms in a category, where composition uses the outputs of the one system as the inputs of another. We thus expect black-boxing to be a functor out of a category of this sort. A ‘black-boxing theorem’ makes this intuition precise.
In an electrical circuit, associated to each wire there is a pair of variables called the potential and current . When we black-box such a circuit, we record only the relation it imposes between the variables on its input and output wires. Since these variables come in pairs, this is a relation between even-dimensional vector spaces. But these vector spaces turn out to be equipped with extra structure: they are symplectic vector spaces, meaning they are equipped with a nondegenerate antisymmetric bilinear form. Black-boxing gives a relation that respects this extra structure: it is a ‘Lagrangian’ relation.
Why does symplectic geometry show up when we black-box an electrical circuit? The first proof of the black-boxing theorem answered this question. A circuit made of linear resistors acts to minimize the total power dissipated in the form of heat. More generally, any circuit made of linear resistors, inductors and capacitors obeys a generalization of this ‘principle of minimum power’. Whenever a system obeys a minimum principle, it establishes a Lagrangian relation between input and output variables. This fact was first noticed in classical mechanics, where systems obey the ‘principle of least action’. Indeed, symplectic geometry has its origins in classical mechanics. But it applies more generally: for any sort of system governed by a minimum principle, black-boxing should give a functor to some category where the morphisms are Lagrangian relations.
The first step toward such a theorem for electrical circuits is to treat circuits as morphisms in a suitable category. We start with circuits made only of ideal perfectly conductive wires. These are morphisms in a prop we call defined in Section 3 of our paper. In Section 8 we construct a black-boxing functor
sending each such circuit to the relation it defines between its input and output potentials and currents. Here is a prop with symplectic vector spaces of the form as objects and linear Lagrangian relations as morphisms, and is a morphism of props. We work in a purely algebraic fashion, so here can be any field.
In Section 9 we extend black-boxing to a larger class of circuits that include linear resistors, inductors and capacitors. This gives a new proof of the black-boxing theorem that Brendan and I proved: namely, there is a morphism of props
sending each such linear circuit to the Lagrangian relation it defines between its input and output potentials and currents. The ease with which we can extend the black-boxing functor is due to the fact that all our categories with circuits as morphisms are props. We can describe these props using generators and relations, so that constructing a black-boxing functor simply requires that we choose where it sends each generator, and check that the all the relations hold. In Section 10 we explain how electric circuits are related to signal-flow diagrams, used in control theory. Finally, in Section 11, we illustrate how props can be used to study nonlinear circuits.
Outline of the results
The paper is pretty long, so here’s a more detailed outline of the results.
In Section 1 we explain a general notion of `-circuit’ that was first introduced under a different name here:
- R. Rosebrugh, N. Sabadini and R. F. C. Walters, Generic commutative separable algebras and cospans of graphs, Theory and Application of Categories 15 (2005), 164–177.
An -circuit is a cospan of finite sets where the apex is the set of nodes of a graph whose edges are labelled by elements of some set In applications to electrical engineering, the elements of describe different ‘circuit elements’ such as resistors, inductors and capacitors. We discuss a symmetric monoidal category whose objects are finite sets and whose morphisms are (isomorphism classes of) -circuits.
In Section 2 we study when is a 1-element set. We call this category simply In applications to engineering, a morphism in describes circuit made solely of ideal conductive wires. We show how such a circuit can be simplified in two successive stages, described by symmetric monoidal functors:
Here is the category of cospans of finite sets, while is the category of ‘corelations’ between finite sets. Corelations, categorically dual to relations, are already known to play an important role in network theory:
- Brendan Fong, Decorated corelations.
Just as a relation can be seen as a jointly monic span, a corelation can be seen as a jointly epic cospan. The functor crushes any graph down to its set of components, while reduces any cospan to a jointly epic one.
In Section 4 we turn to props. Propositions 11 and 12, proved in Appendix A.1 with the help of Steve Lack, characterize which symmetric monoidal categories are equivalent to props and which symmetric monoidal functors are isomorphic to morphisms of props. We use these to find props equivalent to and This lets us reinterpret the arrows here as morphisms of props:
In Section 5 we discuss presentations of props. Proposition 19, proved in Appendix A.2 using a result of Todd Trimble, shows that the category of props is monadic over the category of signatures, This lets us work with props using generators and relations. We conclude by recalling a presentation of due to Lack and a presentation of due to Coya and Fong:
Steve Lack, Composing PROPs, Theory and Applications of Categories 13 (2004), 147–163.
Brandon Coya and Brendan Fong, Corelations are the prop for extraspecial commutative Frobenius monoids, Theory and Applications of Categories 32 (2017), 380–395. (Blog article here.)
In Section 6 we introduce the prop This prop is equivalent to the symmetric monoidal category with finite-dimensional vector spaces over the field as objects and linear relations as morphisms, with direct sum as its tensor product. A presentation of this prop was given in these papers:
Filippo Bonchi, Pawel Sobociénski and Fabio Zanasi, Interacting Hopf algebras, Journal of Pure and Applied Algebra 221 (2017), 144–184.
John Baez and Jason Erbele, Categories in control, Theory and Applications of Categories 30 (2015), 836–881. (Blog article here.)
In Section 7 we state the main result in the paper by Rosebrugh, Sabadini and Walters. This gives a presentation of Equivalently, it says that is the coproduct, in the category of props, of and the free prop on a set of unary operations, one for each element of This result makes it easy to construct morphisms from to other props.
In Section 8 we introduce the prop where morphisms are Lagrangian linear relations between symplectic vector spaces, and we construct the black-boxing functor Mathematically, this functor is the composite
where is a symmetric monoidal functor defined by its action on the generators of In applications to electrical engineering, the black-boxing functor maps any circuit of ideal conductive wires to its ‘behavior’: that is, to the relation that it imposes on the potentials and currents at its inputs and outputs.
In Section 9 we extend the black-boxing functor to circuits that include resistors, inductors, capacitors and certain other linear circuit elements. The most elegant prop having such circuits as morphisms is meaning with the label set taken to be a field We characterize the black-boxing functor
in Theorem 41.
In Section 10 we expand the scope of inquiry to include ‘signal-flow diagrams’, which are important in control theory. We explain how signal-flow diagrams serve as a syntax for linear relations. Concretely, this means that signal-flow diagrams are morphisms in a free prop with the same generators as but no relations. There is thus a morphism of props
mapping any signal-flow diagrams to the linear relation that it denotes. It is natural to wonder how this is related to the black-boxing functor
The answer involves the free prop which arises when we take the simplest presentation of and omit the relations. This comes with a map
which reinstates those relations, and in Theorem 44 we show there is a map of props making this diagram commute:
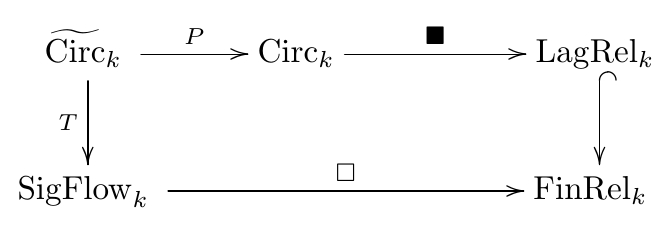
Putting everything together, we get this grand commuting diagram relating circuit diagrams, linear circuits, signal flow diagrams, cospans, corelations, Lagrangian relations, and linear relations:
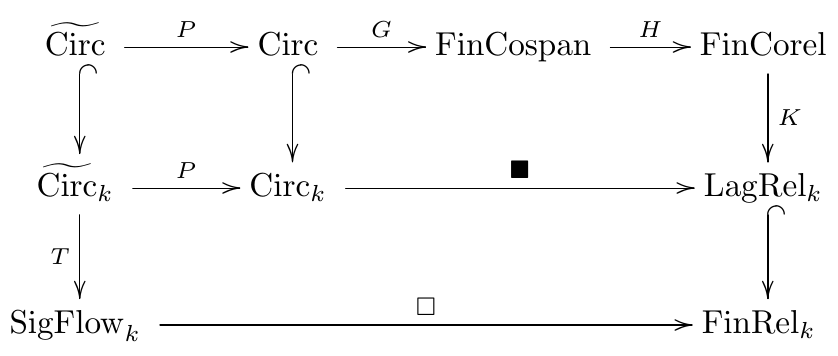
Finally, in Section 11 we illustrate how props can also be used to study nonlinear circuits. Namely, we show how to include voltage and current sources. Black-boxing these gives Lagrangian affine relations between symplectic vector spaces! Eventually we’ll get around to studying more general nonlinear circuits… but not today.


Re: Props in Network Theory
There’s something wrong with the URL for the Joyal and Street paper.