A Problem on Pushouts and Pullbacks
Posted by John Baez
I have a problem involving pullbacks and pushouts. This problem arose in work with Kenny Courser on an application of category theory. But you don’t need to understand anything about that application to understand — and I hope solve! —our problem.
If you can solve it, we will credit you in our paper.
![]()
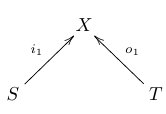
We’re working in the category of finite sets and functions. As you may know, given composable cospans like this:
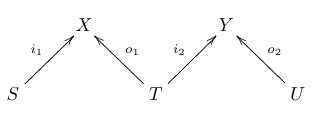
we can compose them using a pushout and get a new cospan:
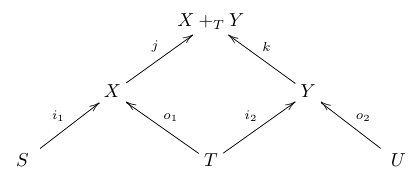
going all the way from to .
Now suppose we have composable maps between cospans, by which I mean commutative diagrams like this:
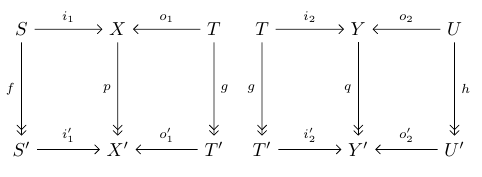
In our application the vertical arrows are all surjections, so I’m noting that in case it helps. We can compose these maps between cospans and get a new map between cospans like this:
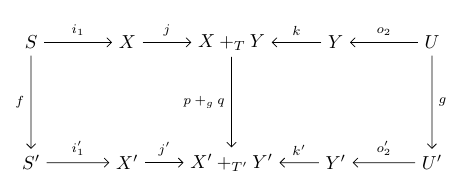
The newly created vertical arrow will again be a surjection.
So far so good. But here’s my problem. I’m also assuming all the squares we start with are pullbacks:

I want to prove that the squares we get are pullbacks:
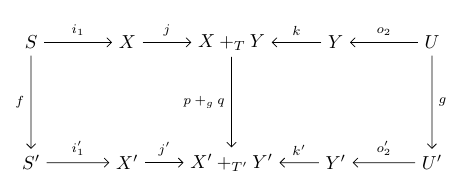
That’s the problem!
Here’s my feeble attempt to solve it. By symmetry it suffices to prove that either one of the squares we get are pullbacks, say the left one. This is the pasting of two smaller squares:
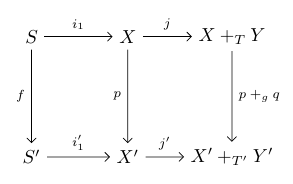
The left-hand smaller square is a pullback, so it suffices —- though perhaps it’s not necessary — to prove that the right-hand smaller square is a pullback.
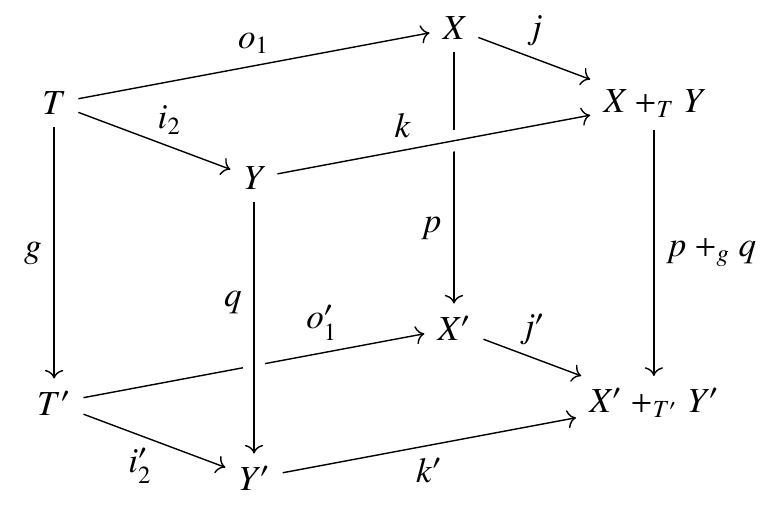
To prove that the right-hand smaller square is a pullback, it may help to contemplate this cube:
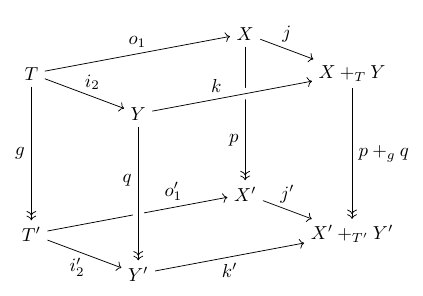
We know that the vertical arrows are surjections, the top and bottom faces are pushouts, and the two left-most faces are pullbacks. We’re trying to prove that the two right-most faces are pullbacks. By symmetry, it’s enough to prove this for either one.
Believe it or not, this sort of situation shows up in the theory of adhesive categories, of which the category of finite sets is an example. People think about a cube like this, with all assumptions except that the vertical squares may not be epic. And in an adhesive category, if either or is monic, we’re done!
That is: when we have the above cube in the category of finite sets, and either or is monic, and the top and bottom faces are pushouts, and the two left-most faces are pullbacks, then the the two right-most faces are pullbacks!
So that’s where I stand, paralyzed with fear. I’m trying to reach the same conclusion, with all the same assumptions except without assuming that or are monic… but I do know that all the vertical arrows in the cube are epic.
That is: if we have the above cube in the category of finite sets, and the vertical arrows are epic, and the top and bottom faces are pushouts, and the two left-most faces are pullbacks, can you show the two right-most faces are pullbacks???
Kenny has looked in vain for counterexamples, so this might actually be true. Or maybe a somewhat different strategy is required. Perhaps somehow the composite square here is a pullback even though the right-hand part is not:

Help! This sort of category theory is not my strong suit.
![]()


Re: A Problem on Pushouts and Pullbacks
I think you can simplify the problem by assuming that , , and are identities.
If the answer to your question is “yes” in general then of course it’s yes in this special case. Conversely, if it’s yes in this special case then it’s yes in general, because the composite of pullback squares is a pullback square (as you observe).
So, you could remove all mention of , , , , , , , , and from the question.