The n-Category Café

Introduction

A few weeks ago here at the Café, Cory and Jade summarized the main ideas behind the DisCoCat model, i.e. the categorical compositional distributional model of meaning developed in a 2010 paper by Coecke, Sadrzadeh, and Clark. Within the comments section of that blog entry, Coecke noted that the DisCoCat model is essentially a grammatical quantum field theory — a functor (morally) from a pregroup to finite dimensional real vector spaces. In this model, the meaning of a sentence is determined by the meanings of its constituent parts, which are themselves represented as vectors with meanings determined statistically. But as he also noted,

Vector spaces are extremely bad at representing meanings in a fundamental way, for example, lexical entailment, like tiger < big cat < mammal < animal can’t be represented in a vector space. At Oxford we are now mainly playing around with alternative models of meaning drawn from cognitive science, psychology and neuroscience. Our Interacting Conceptual Spaces I is an example of this….

This (ICS I) is the paper that we discuss in today’s blog post. It presents a new model in which words are no longer represented as vectors. Instead, they are regions within a conceptual space, a term coined by cognitive scientist Peter Gärdenfors in Conceptual Spaces: The Geometry of Thought. A conceptual space is a combination of geometric domains where convexity plays a key role. Intuitively, if we have a space representing the concept of fruit, and if two points in this space represent banana, then one expects that every point “in between” should also represent banana. The goal of ICS I is to put Gärdenfors’ idea on a more formal categorical footing, all the while adhering to the main principles of the DisCoCat model. That is, we still consider a functor out of a grammar category, namely the pregroup $\mathsf{Preg}(n,s)$, freely generated by noun type $n$ and sentence type $s$. (But in light of Preller’s argument as mentioned previously, we use the word functor with caution.) The semantics category, however, is no longer vector spaces but rather $\mathsf{ConvexRel},$ the category of convex algebras and convex relations. We make these ideas and definitions precise below.

Preliminaries

A convex algebra is, loosely speaking, a set equipped with a way of taking formal finite convex combinations of its elements. More formally, let $A$ be a set and let $D(A)$ denote the set of formal finite sums $\sum_i p_i a_i$ of elements of $A,$ where $p_i\in\mathbb{R}_{\geq 0}$ and $\sum_i p_i=1.$ (We emphasize that this sum is formal. In particular, $A$ need not be equipped with a notion of addition or scaling.) A convex algebra is a set $A$ together with a function $\alpha\colon D(A)\to A$, called a “mixing operation,” that is well-behaved in the following sense:

• the convex combination of a single element is itself, and
• the two ways of evaluating a convex combination of a convex combination are equal.

For example, every convex subspace of $\mathbb{R}^n$ is naturally a convex algebra. (And we can’t resist mentioning that convex subspaces of $\mathbb{R}^n$ are also examples of algebras over the operad of topological simplices. But as we learned through a footnote in Tobias Fritz’s Convex Spaces I, it’s best to stick with monads rather than operads. Indeed, a convex algebra is an Eilenberg-Moore algebra of the finite distribution monad.) Join semilattices also provide an example of convex algebras. A finite convex combination of elements $a_i$ in the lattice is defined to be the join of those elements having non-zero coefficients: $\sum_i p_i a_i:=\vee_i \{a_i:p_i\neq 0\}$. (In particular, the coefficients play no role on the right-hand side.)

Given two convex algebras $(A,\alpha)$ and $(B,\beta)$, a convex relation is a binary relation $R\subseteq A\times B$ that respects convexity. That is, if $R(a_i,b_i)$ for all $i=1,\ldots,n$ then $R\left(\alpha(\sum_{i=1}^n p_i a_i),\beta(\sum_{i=1}^n p_i b_i)\right)$. We then define $\mathsf{ConvexRel}$ to be the category with convex algebras as objects and convex relations as morphisms. Composition and identities are as for usual binary relations.

Now since in this model, the category of vector spaces is being replaced by $\mathsf{ConvexRel}$, one hopes that (in keeping with the spirit of the DisCoCat model), the latter admits a symmetric monoidal compact closed structure. Indeed it does.

• $\mathsf{ConvexRel}$ has a symmetric monoidal structure given by the Cartesian product: We use $(A,\alpha)\otimes(B,\beta)$ to denote the set $A\times B$ equipped with mixing operation given by $$\begin{aligned} D(A\times B)&\longrightarrow A\times B\\ \sum p_i(a_i,b_i)&\mapsto \left(\alpha(\sum p_i a_i),\beta(\sum p_i b_i)\right). \end{aligned}$$ The monoidal unit is the one-point set $\star$ which has a unique convex algebra structure. We’ll denote this convex algebra by $I.$
• Each object in $\mathsf{ConvexRel}$ is self-dual, and cups and caps are given as follows: $$\begin{aligned} \eta_A\colon I \to(A,\alpha)\otimes(A,\alpha) \quad &\text{ is the relation} \quad \{(\star,(a,a)):a\in A)\}\\ \epsilon_A\colon (A,\alpha)\otimes(A,\alpha)\to I \quad &\text{ is the relation} \quad \{((a,a),\star):a\in A\} \end{aligned}$$

The compact closed structure guarantees that $\mathsf{ConvexRel}$ fits nicely into the DisCoCat framework: words in a sentence are assigned types according to a chosen pregroup grammar, and a sentence is deemed grammatical if it reduces to type $s$. Moreover, these type reductions in $\mathsf{Preg}(n,s)$ give rise to corresponding morphisms in $\mathsf{ConvexRel}$ where the meaning of the sentence can be determined. We’ll illustrate this below by computing the meaning of the sentence

$$b a n a n a s\; t a s t e\; s w e e t.$$

To start, note that this sentence is comprised of three grammar types:

and each corresponds to a different conceptual space $$\text{noun, }\; n \rightsquigarrow N \qquad\qquad \text{sentence, }\; s \rightsquigarrow S \qquad\qquad \text{verb, }\; n^r s n^l \rightsquigarrow N\otimes S \otimes N$$ which we describe next.

Computing Meaning

The Noun Space $N$

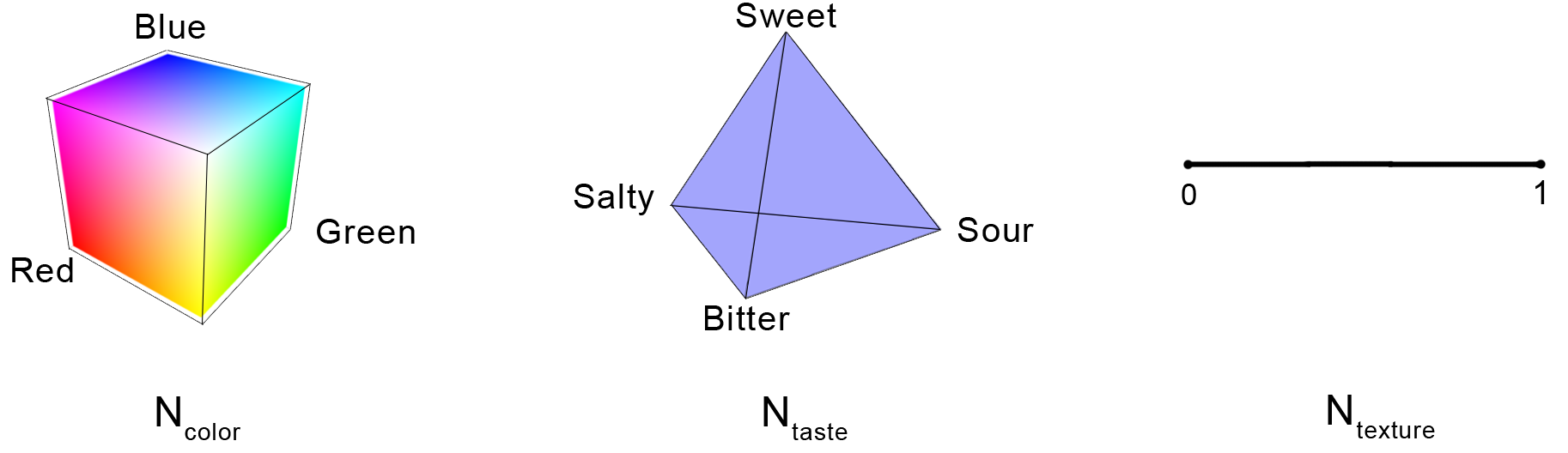
A noun is a state $I\to N$, i.e. a convex subset of the noun space $N$. Restricting our attention to food nouns, the space $N$ is a product of color, taste, and texture domains: $$N=N_{\text{color}}\otimes N_{\text{taste}}\otimes N_{\text{texture}} \subset \mathbb{R}^8$$ where

• $N_{\text{color}}$ is the RGB color cube, i.e. the set of all triples $(R,G,B)\in [0,1]^3$.
• $N_{\text{taste}}$ is the taste tetrahedron, i.e. the convex hull of four basic tastes: sweet, sour, bitter, and salty.
• $N_{\text{texture}}$ is the unit interval $[0,1]$ where 0 represents liquid and 1 represents solid.

The noun banana is then a product of three convex subregions of $N$:

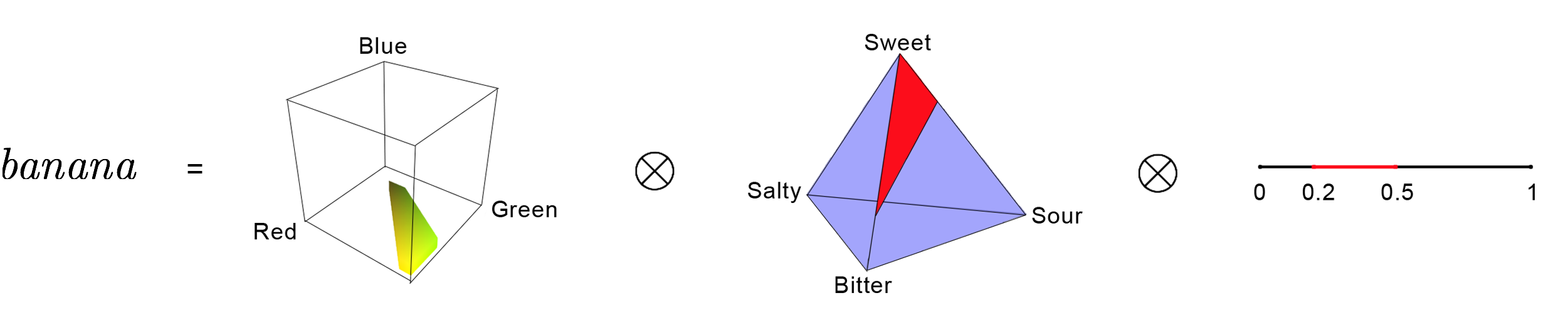
That is, banana is the product of a yellow/green region, the convex hull of three points in the taste tetrahedron, and a subinterval of the texture interval. Other foods and beverages, avocados, chocolate, beer, etc. can be expressed similarly.

The Sentence Space $S$

The meaning of a sentence is a convex subset of a sentence space $S$. Here, $S$ is chosen as a simple-yet-sensible space to capture one’s experience when eating and drinking. It is the join semilattice on four points

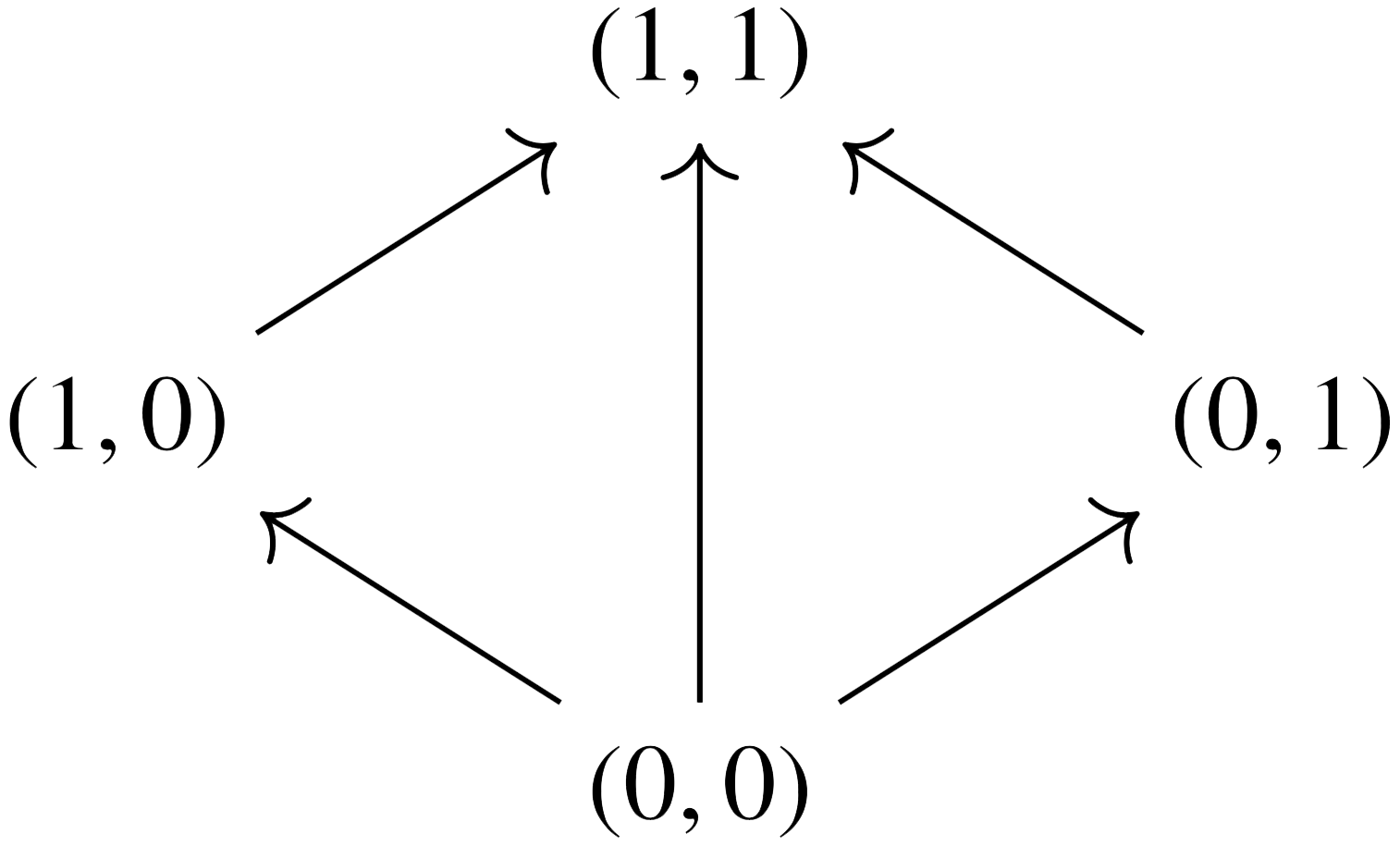
where in the first component, 0 = negative and 1 = positive, while in the second component, 0 = not surprising and 1 = surprising. For instance, $(0,1)$ represents negative and surprising while the convex subset $\{(1,1),(1,0)\}$ represents positive.

The Verb Space $N\otimes S\otimes N$

A transitive verb is a convex subset of $N\otimes S\otimes N$. For instance, if we suppose momentarily that we live in a world in which one can survive on bananas and beer alone, then the verb taste can be represented by $$\begin{aligned} t a s t e &= \text{Conv}( \{g r e e n\; b a n a n a \otimes\{(0,0)\}\otimes b i t t e r\}\\ &\,\cup \{g r e e n\; b a n a n a\otimes\{(1,1)\}\otimes s w e e t\}\\ &\,\cup \{y e l l o w\; b a n a n a\otimes\{(1,0)\}\otimes s w e e t\}\\ &\,\cup \{b e e r \otimes\{(0,1)\}\otimes s w e e t\}\\ &\,\cup \{b e e r\otimes\{(1,0)\}\otimes b i t t e r\}) \end{aligned}$$ where Conv denotes the convex hull of the argument. Here, green is an intersective adjective, so green banana is computed by taking the intersection of the banana space with the green region of the color cube. Likewise for yellow banana.

Tying it all together

Finally, we compute the meaning of bananas taste sweet, which has grammar type reduction $n(n^r s n^l)n\leq (nn^r )s\leq s.$ In $\mathsf{ConvexRel}$, this corresponds to the following morphism: $$\overset{\text{bananas}}{N}\otimes\;\; \overset{\text{taste}}{N\;\; \otimes \;\; S\;\; \otimes \;\;N}\;\; \otimes \overset{\text{sweet}}{N}\;\;\;\overset{\epsilon_N\otimes 1_S\otimes\epsilon_N}{\longrightarrow}\;\;\; S$$ $$\begin{aligned} b a n a n a s\; t a s t e\; s w e e t &= (\epsilon_N\otimes 1_S\otimes \epsilon_N)(b a n a n a s \otimes t a s t e \otimes s w e e t)\\ &=(\epsilon_N\otimes 1_S)(b a n a n a\otimes (g r e e n\; b a n a n a \otimes \{(1,1)\} \\ &\qquad\qquad\qquad\qquad\quad \cup y e l l o w\; b a n a n a \otimes\{(1,0)\} \\ &\qquad\qquad\qquad\qquad\quad \cup b e e r\otimes\{(0,1)\}))\\ &=\{(1,1),(1,0)\}\\ &= p o s i t i v e \end{aligned}$$ Note that the rightmost $\epsilon_N$ selects subsets of the taste space that include sweet things and then deletes “sweet.” The leftmost $\epsilon_N$ selects subsets of the taste space that include banana and then deletes “banana.” We are left with a convex subset of $S$, i.e. the meaning of the sentence.

Closing Remarks

Although not shown in the example above, one can also account for relative pronouns using certain morphisms called multi-wires or spiders (these arise from commutative special dagger Frobenius structures). The authors also give a toy example from the non-food world by modeling movement of a person from one location to another, using time and space to define new noun, sentence, and verb spaces.

In short, the conceptual spaces framework seeks to capture meaning in a way that resembles human thought more closely than the vector space model. This leaves us to puzzle over a couple of questions: 1) Do all concepts exhibit a convex structure? and 2) How might the conceptual spaces framework be implemented experimentally?