Linguistics Using Category Theory

February 6, 2018

Posted by John Baez

$MathML-enabled post (click for more details).$

guest post by Sarah Griffith and Jade Master

Most recently, the Applied Category Theory Seminar took a step into linguistics by discussing the 2010 paper Mathematical Foundations for a Compositional Distributional Model of Meaning, by Bob Coecke, Mehrnoosh Sadrzadeh, and Stephen Clark.

Here is a summary and discussion of that paper.

$MathML-enabled post (click for more details).$

In recent years, well known advances in AI, such as the development of AlphaGo and the ongoing development of self driving cars, have sparked interest in the general idea of machines examining and trying to understand complex data. In particular, a variety of accounts of successes in natural language processing (NLP) have reached wide audiences (see, for example, The Great AI Awakening).

One key tool for NLP practitioners is the concept of distributional semantics. There is a saying due to Firth that is so often repeated in NLP papers and presentations that even mentioning its ubiquity has become a cliche:

“You shall know a word by the company it keeps.”

The idea is that if we want to know if two words have similar meanings, we should examine the words they are used in conjunction with, and in some way measure how much overlap there is. While direct ancestry of this concept can be traced at least back to Wittgenstein, and the idea of characterizing an object by its relationship with other objects is one category theorists are already fond of, distributional semantics is distinguished by its essentially statistical methods. The variations are endless and complex, but in the cases relevant to our discussion, one starts with a corpus, a suitable way of determining what the context of a word is (simply being nearby, having a grammatical relationship, being in the same corpus at all, etc) and ends up with a vector space in which the words in the corpus each specify a point. The distance between vectors (for an appropriate definition of distance) then correspond to relationships in meaning, often in surprising ways. The creators of the GloVe algorithm give the example of a vector space in which $king - man + woman = queen$ .

There is also a “top down,” relatively syntax oriented analysis of meaning called categorial grammar. Categorial grammar has no accepted formal definition, but the underlying philosophy, called the principle of compositionality, is this: a meaningful sentence is composed of parts, each of which itself has a meaning. To determine the meaning of the sentence as a whole, we may combine the meanings of the constituent parts according to rules which are specified by the syntax of the sentence. Mathematically, this amounts to constructing some algebraic structure which represents grammatical rules. When this algebraic structure is a category, we call it a grammar category.

The Paper

Preliminaries

Pregroups are the algebraic structure that this paper uses to model grammar. A pregroup P is a type of partially ordered monoid. Writing $x \to y$ to specify that $x \leq y$ in the order relation, we require the following additional property: for each $p \in P$ , there exists a left adjoint $p^l$ and a right adjoint $p^r$ , such that $p^l p \to 1 \to p p^r$ and $p p^r \to 1 \to p^r p$ . Since pregroups are partial orders, we can regard them as categories. The monoid multiplication and adjoints then upgrade the category of a pregroup to compact closed category. The equations referenced above are exactly the snake equations.

We can define a pregroup generated by a set $X$ by freely adding adjoints, units and counits to the free monoid on $X$ . Our grammar categories will be constructed as follows: take certain symbols, such as $n$ for noun and $s$ for sentence, to be primitive. We call these “word classes.” Generate a pregroup from them. The morphisms in the resulting category represent “grammatical reductions” of strings of word classes, with a particular string being deemed “grammatical” if it reduces to the word class $s$ . For example, construct the pregroup $Preg( \{n,s\})$ generated by $n$ and $s$ . A transitive verb can be thought of as accepting two nouns, one on the left and one on the right, and returning a sentence. Using the powerful graphical language for compact closed categories, we can represent this as

Using the adjunctions, we can turn the two inputs into outputs to get

Therefore the type of a verb is $n^r s n^l$ . Multiplying this on the left and right by $n$ allows us to apply the counits of $n$ to reduce $n \cdot (n^r s n^l) \cdot n$ to the type $s$ , as witnessed by

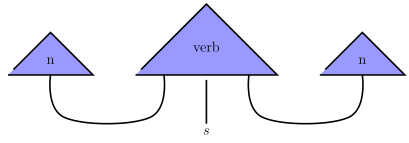
Let $(\mathbf{FVect},\otimes, \mathbb{R})$ be the symmetric monoidal category of finite dimensional vector spaces and linear transformations with the standard tensor product. Since any vector space we use in our applications will always come equipped with a basis, these vector spaces are all endowed with an inner product. Note that $\mathbf{FVect}$ has a compact closed structure. The counit is the diagonal

$\begin{array}{cccc} \eta_l = \eta_r \colon & \mathbb{R} & \to &V \otimes V \\ &1 &\mapsto & \sum_i \overrightarrow{e_i} \otimes \overrightarrow{e_i} \end{array}$

and the unit is a linear extension of the inner product

$\begin{array}{cccc} \epsilon^l = \epsilon^r \colon &V \otimes V &\to& \mathbb{R} \\ & \sum_{i,j} c_{i j} \vec{v_{i}} \otimes \vec{w_j} &\mapsto& \sum_{i,j} c_{i j} \langle \vec{v_i}, \vec{w_j} \rangle. \end{array}$

The Model of Meaning

Let $(P, \cdot)$ be a pregroup. The ingenious idea that the authors of this paper had was to combine categorial grammar with distributional semantics. We can rephrase their construction in more general terms by using a compact closed functor

$F \colon (P, \cdot) \to (\mathbf{FVect}, \otimes, \mathbb{R}) .$

Unpacking this a bit, we assign each word class a vector space whose basis is a chosen finite set of context words. To each type reduction in $P$ , we assign a linear transformation. Because $F$ is strictly monoidal, a string of word classes $p_1 p_2 \cdots p_n$ maps to a tensor product of vector spaces $V_1 \otimes V_2 \otimes \cdots \otimes V_n$ .

To compute the meaning of a string of words you must:

Assign to each word a string of symbols $p_1 p_2 \cdots p_n$ according to the grammatical types of the word and your choice of pregroup formalism. This is nontrivial. For example, many nouns can also be used as adjectives.
Compute the correlations between each word in your string and the context words of the chosen vector space (see the example below) to get a vector $v_1 \otimes \cdots \otimes v_n \in V_1 \otimes \cdots \otimes V_n$ ,
choose a type reduction $f \colon p_1 p_2 \cdots p_n \to q_1 q_2 \cdots q_n$ in your grammar category (there may not always be a unique type reduction) and,
apply $F(f)$ to your vector $v_1 \otimes \cdots \otimes v_n$ .
You now have a vector in whatever space you reduced to. This is the “meaning” of the string of words, according the your model.

This sweeps some things under the rug, because A. Preller proved that strict monoidal functors from a pregroup to $\mathbf{FVect}$ actually force the relevant spaces to have dimension at most one. So for each word type, the best we can do is one context word. This is bad news, but the good news is that this problem disappears when more complicated grammar categories are used. In Lambek vs. Lambek monoidal bi-closed categories are used, which allow for this functorial description. So even though we are not really dealing with a functor when the domain is a pregroup, it is a functor in spirit and thinking of it this way will allow for generalization into more complicated models.

An Example

As before, we use the pregroup $Preg(\{n,s\})$ . The nouns that we are interested in are

$\{ Maria, John, Cynthia \}$

These nouns form the basis vectors of our noun space. In the order they are listed, they can be represented as

$\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}.$

The “sentence space” $F(s)$ is taken to be a one dimensional space in which $0$ corresponds to false and the basis vector $1_S$ corresponds to true. As before, transitive verbs have type $n^r s n^l$ , so using our functor $F$ , verbs will live in the vector space $N \otimes S \otimes N$ . In particular, the verb “like” can be expressed uniquely as a linear combination of its basis elements. With knowledge of who likes who, we can encode this information into a matrix where the $i j$ -th entry corresponds to the coefficient in front of $v_i \otimes 1_s \otimes v_j$ . Specifically, we have

$\begin{bmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}.$

The $i j$ -th entry is $1$ if person $i$ likes person $j$ and $0$ otherwise. To compute the meaning of the sentence “Maria likes Cynthia”, you compute the matrix product

$\begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix} =1$

This means that the sentence “Maria likes Cynthia” is true.

Food for Thought

As we said above, this model does not always give a unique meaning to a string of words, because at various points there are choices that need to be made. For example, the phrase “squad helps dog bite victim” has a different meaning depending on whether you take “bite” to be a verb or a noun. Also, if you reduce “dog bite victim” before applying it to the verb, you will get a different meaning than if you reduce “squad helps dog” and apply it to the verb “bite”. On the one hand, this a good thing because those sentences should have different meanings. On the other hand, the presence of choices makes it harder use this model in a practical algorithm.

Some questions arose which we did not have a clear way to address. Tensor products of spaces of high dimension quickly achieve staggering dimensionality — can this be addressed? How would one actually fit empirical data into this model? The “likes” example, which required us to know exactly who likes who, illustrates the potentially inaccessible information that seems to be necessary to assign vectors to words in a way compatible with the formalism. Admittedly, this is a necessary consequence of the fact the evaluation is of the truth or falsity of the statement, but the issue also arises in general cases. Can this be resolved? In the paper, the authors are concerned with determining the meaning of grammatical sentences (although we can just as easily use non-grammatical strings of words), so that the computed meaning is always a vector in the sentence space $F(s)$ . What are the useful choices of structure for the sentence space?

This paper was not without precedent — suggestions and models related its concepts of this paper had been floating around beforehand, and could be helpful in understanding the development of the central ideas. For example, Aerts and Gabora proposed elaborating on vector space models of meaning, incidentally using tensors as part of an elaborate quantum mechanical framework. Notably, they claimed their formalism solved the “pet fish” problem - English speakers rate goldfish as very poor representatives of fish as a whole, and of pets as a whole, but consider goldfish to be excellent representatives of “pet fish.” Existing descriptions of meaning in compositional terms struggled with this. In The Harmonic Mind, first published in 2005, Smolensky and Legendre argued for the use of tensor products in marrying linear algebra and formal grammar models of meaning. Mathematical Foundations for a Compositional Distributional Model of Meaning represents a crystallization of all this into a novel and exciting construction, which continues to be widely cited and discussed.

We would like to thank Martha Lewis, Brendan Fong, Nina Otter, and the other participants in the seminar.

Posted at February 6, 2018 7:18 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3016

44 Comments & 0 Trackbacks

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

In The Harmonic Mind, first published in 2005, Smolensky and Pulman argued

Shouldn’t that be “Smolensky and Legendre”? Stephen Pulman is involved in the field but didn’t author that book.

Also I would like to point out that in this perspective meaning is conflated with truth-conditional semantics which might be regarded as a sanity check on grammars that contain quantifiers and maybe modalities and at best allow inferences on the truth of sets of sentences to conclude things like “Socrates is mortal”. I am unaware of any applied NLP system that uses truth inference. In a system for for language translation this notion of “meaning” becomes just figuring out for a string of words their most likely word classes, senses, and grammatical relations between them.

Often what can be considered the meaning of a sentence involves filling in implicit information. For example the meaning of the sentence:

“Mary pulled her car up and got out”

should contain

“Mary was inside her car driving it. She stopped the car and then she moved to just outside her car”

Different languages have different strategies for how to leave information implicit.

Posted by: RodMcGuire on February 6, 2018 10:23 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Well there’s a coincidence! As Richard says below, I’ve been looking at homotopy type theory as a tool for natural language. As well as treating the ‘the’ of definite description, I just gave a talk this week on ‘and’. This takes up examples like your “Mary pulled her car up and got out”.

Here are the slides.

Posted by: David Corfield on February 8, 2018 12:28 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Shouldn’t that be “Smolensky and Legendre”? Stephen Pulman is involved in the field but didn’t author that book.

Yes. Thank you for noticing this, I will change it :).

Also I would like to point out that in this perspective meaning is conflated with truth-conditional semantics

As far as I can tell so far this model has only been used for truth-conditional semantics in the way that you describe. However, I believe that it can be generalized to more complicated meanings than just “true or false”. You can choose any set of meanings that can fit into a vector space.

You are right that this model has no way to fill in all the implicit assumptions in “Mary pulled her car up and got out”. But I don’t think the situation is hopeless. I think the best way to go about it would be to alter the model in a way that allows it to respond to data. I think that the meaning of the sentence above could potentially be trained into the model with a machine learning algorithm.

Posted by: Jade Master on February 9, 2018 5:27 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thank you for your comments!

I don’t believe it was the intent of the authors that their framework require meaning to be interpreted in a truth-conditional semantic sense (for one thing, I don’t see this sentiment in Bob Coecke’s very educational comments). However, that concept of meaning probably makes the paper a lot more readable. In the example we described in the blog post, I don’t see any reason why the entries of the matrix couldn’t have been populated to reflect, say, word co-occurrence in a corpus, or in some other way - but then you have the additional question of whether this gets the model to describe something you want, which is probably more than the authors want to get into in this initial paper. In particular, the question of determining what the “sentence space” ought to be seems like it would become involved as you try to upgrade to more sophisticated concepts of meaning.

Posted by: Cory Griffith on February 11, 2018 9:05 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

In the paper, there are some remarks about the relationship to Montague semantics. Though I have not studied the paper closely, this seems a little weak to me at first sight: Montague semantics is able to give an explanation of how to formally (i.e. not in an ad hoc way) view many aspects of natural language semantics as being built up using logical connectives, quantifiers, etc.

As far as I see, no explanation of any of this logical layer is given in the paper; there is even a remark that ‘basic’ aspects such as conjunction might be subtle. Has any progress been made on this since?

I think of Montague semantics as a yardstick for any new theory of natural language semantics. It is one thing to explain in an ad hoc way the meaning of some particular natural language expression. David Corfield has been doing interesting investigations of this kind in the setting of HoTT, and it can of course be very interesting, e.g. for philosophy. But it is quite another thing to have a semantical theory which formally attaches meaning to anything, and which does so in a way which is reasonable in many cases, and which adheres to the principle of compositionality. Montague makes it very clear that breaking from the ad hoc to the formal is a (maybe the) principal motivation for his work.

Of course Montague semantics is not perfect, and lots of work has been done since. I would love to see category theory or higher category theory shed light on it, or give an alternative. I have thought a bit about it myself from time to time.

Posted by: Richard Williamson on February 7, 2018 8:51 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Montague semantics can to some extend be seen as an instance of our model, simply by taking matrices over the Booleans rather than over the positive reals i.e. we move to relations. Now, matrices over the positive reals within their Boolean realm come with a lot of logical operations, which is what makes Montague work. Unfortunately, leaving the Boolean realm most of that goes, e.g. while in the world of relations there is a perfect not matrix, this is not the case when taking matrices over most other semi-rings. But if we take meaning serious, a truth-based semantics simply won’t do, and that’s why in practical NLP nobody uses Montague.

We have some ideas on how to bring logic back in and the key is to not stick to vector space models. We’ve done some work with density matrices where one regains some “quantum logical” structure, and Gardeners’ conceptual spaces could really be the way forward.

Posted by: bob on February 10, 2018 10:30 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thank you for your thoughts!

What I was getting at was not that there is no relation at all between the boolean version of the semantics in the paper and the Montague semantics, but that the relationship seems weak to me. After all, the idea to view meaning through relations is very old; Montague’s contribution was to find a way to refine this so that one has a theory which ‘properly’ accounts for certain linguistic phenomena. In particular, one does not, in the Montague semantics, simply assign some piece of a sentence a truth value and combine these truth values according to the logical rules; this is precisely the ‘na¯ve’ approach that Montague moved away from.

This is not to disagree that something richer than a truth value could be very useful, of course.

Posted by: Richard Williamson on February 12, 2018 2:53 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I should add to this that the failure to accommodate logical connectives in a Boolean manner may be a feature rather than a bug. Most uses of AND, NOT, OR in language are by no means Boolean, and even depending on its meaning, so probably has an empirical component besides a structural one.

If one says: I don’t want a red car, one doesn’t mean any colour besides perfect RGB-red in the colour spectrum. On the other hand, a graphic designer may precisely mean that.

As AND, OR are concerned, the two ANDs and ORs of linear logic all are in use, that is, both are available but you only can pick one vs both are available and you can pick both (AND, OR then differing in terms of you actually having a choice).

Posted by: bob on February 10, 2018 11:30 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I don’t know anything about Montague semantics, but all of a sudden I’m curious about how linguists try to formalize the notion of the “meaning” of a sentence.

We can think of logical systems like the predicate calculus as rather impoverished and rigid forms of human language. For these systems there’s been intensive mathematical work attempting to formalize the notion of “meaning”, e.g. through model theory and functorial semantics. The basic idea is to cook up some sort of map that sends pieces of sentences, and eventually whole sentences, to things that can serve as their “meanings”.

But the predicate calculus is mainly about statements, that is, assertions. Human language has other kinds of sentences, the most famous being questions and commands. How can we formalize the “meaning” of these other kinds of sentences?

(And how many kinds are there? Do languages I’m unfamiliar with have kinds of sentences that I’ve never even dreamt of? That would be exciting!)

Posted by: John Baez on February 8, 2018 6:06 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

We can think of logical systems like the predicate calculus as rather impoverished and rigid forms of human language.

Montague’s point of view, which I think it is fair to say was quite revolutionary, was that they are not in fact impoverished; there is a very well-known quote of his in which he suggests that there is ‘no important theoretical difference’ between natural language and the artificial language of a logician.

For these systems there’s been intensive mathematical work attempting to formalize the notion of “meaning”, e.g. through model theory and functorial semantics.

Montague used exactly this, i.e. model theory, to express his formalism. His background was in mathematical logic (I believe his PhD supervisor was Tarski).

He makes heavy use of modal and higher-order logic, though.

Human language has other kinds of sentences, the most famous being questions and commands. How can we formalize the “meaning” of these other kinds of sentences?

I think the first point to make is that the most common type of natural language sentences are in fact ‘declarative’, i.e. make an assertion, like in the predicate calculus. So it is not unreasonable to restrict one’s attention to this initially, and this is what Montague did.

However, he did make some remarks on non-declarative sentences, and work has been done on this since, though I do not know it very well.

And how many kinds are there?

One can at least add exclamatory sentences to the list. It has been argued that there are no kinds other than these three, though I do not know whether that argument is restricted to English.

Posted by: Richard Williamson on February 8, 2018 9:17 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

It’s worth noting that real-world mathematics involves questions (is $P$ true?) and commands (let $P$ be true) as well as assertions ( $P$ is true), though many of the commands are ‘type declarations’.

I tend to think of exclamations as abbreviated, highly emotional assertions. Maybe this is naive.

Though I could be blinded by my culture, it seems there’s something fundamental about the trio of questions, commands and assertions. If something like this is really true, it should be possible to understand it mathematically.

Strangely, while computer programmers are much closer to having formalized the theory of commands than traditional mathematicians (e.g. they often use different symbols for “ $x$ is equal to $y$ ” and “let $x$ equal $y$ ”), the programming languages I know are still pretty limited when it comes to questions. Until recently, the paradigm was to boss the computer around rather than to interact with it in a more equal way, which requires questions. Recently, digital assistants have learned how to understand some questions….

Posted by: John Baez on February 8, 2018 3:58 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I tend to think of exclamations as abbreviated, highly emotional assertions.

I think that things like ‘Oh my goodness!’, or ‘Hurray!’, or ‘Hmm.’ probably don’t fit into that category, but I agree that it is difficult to say anything beyond a few words that is exclamatory but not an assertion or question.

it seems there’s something fundamental about the trio of questions, commands and assertions. If something like this is really true, it should be possible to understand it mathematically.

I really like the idea of trying to understanding something like this mathematically; it does indeed seem tailor-made for mathematics.

the programming languages I know are still pretty limited when it comes to questions.

Indeed, although maybe one could see something like an if block as question-like.

Posted by: Richard Williamson on February 8, 2018 10:39 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

It’s interesting to note other potential categories, like declarations. For example, the sentence “this meeting is adjourned” is not so much a true/false statement, as it is used to make itself true by the very act of its saying. John Searle has written a lot of interesting things about these kinds of speech acts.

Posted by: Callum Hackett on February 9, 2018 5:52 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Persuasion is an extraordinarily important form of speech that mathematicians are not very good at thinking about—since we often play a game where we pretend that ‘proof’ is the only form of persuasion that counts.

Grammatically, persuasion consists of a mixture of assertions, questions and commands:

“I’d like some money.”

“Could you give me some money?”

“Please give me some money.”

but somehow the grammatical form of the sentence scarcely matters!

Posted by: John Baez on February 9, 2018 6:01 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I haven’t read this all yet, but just one terminological note: I believe that nearly always a “compact closed” category means one that is symmetric monoidal (and all objects have duals). A non-symmetric monoidal category in which all object have both left and right duals is more often called rigid or autonomous.

Posted by: Mike Shulman on February 8, 2018 4:08 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

That’s indeed the most common convention, and I’m happy with it, but I just bumped into this paper:

A. Preller and J. Lambek, Free compact 2-categories, Mathematical Structures in Computer Science 17 (2005), 309-340.

and they say a 2-category is compact if every 1-morphism has both a left and right adjoint. So maybe some categorical linguists use this convention, which then could apply to monoidal categories as a special case.

Anyway, it looks like an interesting paper!

Posted by: John Baez on February 9, 2018 6:55 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I thought I’d give a few notes here speaking as a linguist. I’m very much interested in this kind of work and believe it has some applicability to linguistic theory, but though I don’t quite have the expertise to understand every facet of this, I do think its applicability is not quite what people think it to be.

Here’s one issue. Categorial grammar embodies an approach to the constitution of our mental lexicons known as ‘lexicalism’, whose major claim is that words are listed in our minds with certain satisfaction conditions that must be adhered to in the building of syntactic structure. An example of this is the above discussion of transitive verbs - it is a fundamentally lexicalist conception of language to imagine that verbs are intrinsically defined as having (even variable) transitivity requirements, such that a verb can only be deployed grammatically if, say, it is listed as transitive and appears with exactly two arguments of the right kind.

Over the past 15 years or so, many (though not all) linguists have been leading a push-back against lexicalism. For anti-lexicalists, verbs are no longer to be thought of has having intrinsic argument structure requirements, and, in fact, strange as this may sound, there are NO words that are even intrinsically verbs. Instead, our mental lexicons consist of a list of atomic, non-categorial meaning units that we can place in, say, a pre-determined, templatic verbal structure, which in such a context will force a reading of that unit as verbal. Do the same with a templatic nominal structure, though, and it becomes a noun.

The restrictions here are semantic, rather than syntactic. Thus, if we find a verb like ‘kill’ with three arguments instead of the expected two, its unacceptability is said to derive from the impossibility of its meaningful interpretation given background world knowledge, rather than from the violation of grammatical requirements of the word (as these don’t exist in the theory). There are lots of detailed arguments in support of this position, but its major successes are in accounting for certain structural universals across languages, and in accounting for the sheer flexibility of words, which is often underplayed in lexicalist models.

Quite possibly, what we’re looking at with notions such as ‘transitive verb’ are merely powerful, fossilised conventions. If the reality is that there are no inherently transitive verbs, but only ‘words that are often used verbally and transitively’, then an approach based on lexicalism, like categorial grammar, will always amount to a retrospective model of some specific linguistic system at some fixed point in history, rather than a theory of the cognitive reality of language.

There is a broader (potential) problem here, though you may be pleased to hear that it’s severe even in linguistics! It has always been supposed - because it seems so obvious - that words in linguistic utterances, understood as units of sound, correspond to conceptual units in a compositional semantics, however that semantics ought to be logically modelled. However, analogous to the point I made just above, the correspondences that we perceive in everyday communication between words and concepts are turning out in many theories to be retrospective conveniences that do not properly delimit words’ true denotations.

The upshot of this view (known as ‘meaning eliminativism’ in a branch of pragmatics called ‘relevance theory’), is that words in contexts of use are excellent for referring to concepts, but words themselves do not achieve this by denoting concepts. Instead, words have non-conceptual potentials for conceptual reference, and humans use their pragmatic capacities to fix conceptual referents in context (it is too much to discuss here, but it is important to note that a non-conceptual potential is something quite different from polysemy, which is just a many-to-one correspondence between a word and possible concepts - the claim is instead that words denote something that is materially different from conceptual concept, though use of a word is perceived to have conceptual reference).

If this is true, then the conclusion we would have to draw is that distributional models of meaning are fabulous, insightful descriptions of the structure of word denotations, but because word denotations are not conceptual, and because it is concepts that must enter into semantic composition, then they cannot be models of semantics. Of course, this requires a severance of word meaning from semantics, but that is exactly the radical possibility that is on the horizon in linguistic theory at present.

Posted by: Callum Hackett on February 9, 2018 1:07 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Very interesting. Thanks.

Something I’ve been looking into recently is event semantics. I’ve seen there arguments in agreement with yours that we shouldn’t see particular verbs as playing specific lexical roles in event descriptions, but rather should look to the structural frameworks in which they participate.

I’ve become quite attached to Moens and Steadman’s event nucleus construction. Would you be able to say how this approach is received by linguists?

Posted by: David Corfield on February 9, 2018 8:32 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

You’re absolutely right that event semantics has lots of relevance for these issues. Strictly speaking, there’s nothing preventing a lexicalist model of event structure, but I do think that the varieties of evidence for what Moens and Steedman call ‘coercion’ really compel us to look at alternatives, where, just as you say, interpretations are derived from the structures in which words participate. In the semantics circles I move in, I haven’t seen Moens’ and Steedman’s framework referenced, but it seems to me that there have been independent developments of the same ideas, as their suggestions are thoroughly compatible with what other linguists are saying.

Posted by: Callum Hackett on February 9, 2018 5:41 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

The general approach in Steedman and Moens’ handout reminds me a lot of this classic 1998 article by Henrietta de Swart:

https://www.jstor.org/stable/4047954

She references Moens’ thesis. I’m not sure how much things have moved on since then, but Carlota Smith’s (1991) The Parameter of Aspect seemed to me to take a fundamentally different view of things, which probably still has its advocates.

Posted by: Avery Andrews on February 11, 2018 2:33 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Here is something both large and recent, citing both de Swart and something by Moens & Steedman, so it might be a good resource for getting up to speed on aspect and coercion:

http://semanticsarchive.net/Archive/TRiZTY1M/EventsStatesTimes_Altshuler.pdf

Btw for those who want to fish around in the linguistics literature, the semantics archive and lingbuzz.auf.net are useful.

Posted by: Avery Andrews on February 11, 2018 2:58 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

In case anyone ever follows up this line of thought, I gave treated this event nucleus construction in my book, Modal Homotopy Type Theory, pp. 66-71.

Posted by: David Corfield on July 12, 2023 10:00 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I didn’t realise that we often mark Moens and Steedman’s iteration operator in English by the suffix ‘-le’. So crack $\to$ crackle, daze $\to$ dazzle, game $\to$ gamble, etc. (more here).

Posted by: David Corfield on April 13, 2024 8:45 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thanks I really enjoyed reading your response. I learned a lot and I think that I finally understood why its called categorial instead of categorical grammar. The category part of the word refers to the assumption that all words fit into a well defined word class and not to category theory.

The first issue that you bring up is,

For anti-lexicalists, verbs are no longer to be thought of has having intrinsic argument structure requirements

This is great! I mean it is not great for DisCoCat models but it helps me understand some of my thoughts about them. To me this suggests that instead of a word space for each word class, every word should be treated on equal footing and live a common meaning space. I am not sure how this would work…but there should some way to apply a Lambek grammar to that meaning space which starts with arbitrary words as representatives for each word class. Alternatively, there should be some way to think of the meaning space for a word class as the meaning space for a different word class.

The next problem is that

words in contexts of use are excellent for referring to concepts, but words themselves do not achieve this by denoting concepts.

This is a very interesting idea which reminds me of the Platonic Theory of Forms. A word will have a different meaning in every context so it is impossible to accurately represent it as a single vector in a vector space. I am less optimistic about being able to incorporate this sort of flexibility into a DisCoCat model. However, there may be ways to get a little bit closer to this. In Interacting Conceptual Spaces I, the authors use convex algebras instead of vector spaces. In vague terms this models words as subsets of some conceptual space. This allows the words to take on a range of values rather than just one as it would in a vector space.

Posted by: Jade Master on February 9, 2018 6:47 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

This was very informative - thank you. I’m curious about the scope of the disagreement within linguistics. Does the anti-lexicalist interpretation of language take lexicalist interpretations to be wrong broadly, or good approximations that unfortunately do not capture important special cases? To illustrate what I mean, an example of the former might be Aristotle’s cosmology, whereas an example of the latter might be Newton’s laws.

I ask this because DisCoCat (what we outline in the post) involves ideas that seem to come from domains with very different standards of success. You mention the possibility that lexicalist theories will always be snapshots of linguistic moments in history - but a particular vector space model of meaning is also going to be a snapshot, so regardless of whether our syntactic formalism captures language generally, we should never expect a particular application of DisCoCat to be more than a snapshot as well. In this light, the specificity of a formalism to particular languages and/or times could just be a consequence of it being well adapted to the task at hand.

Posted by: Cory Griffith on February 12, 2018 12:41 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I have been interested in this topic, but I think it doesn’t yet address some of the key things I want in a theory of meaning of sentences. Consider two sentences with nearly the same meaning but different structure: “The firefighter rescued the cat” vs. “The cat was saved by the person fighting the fire.” How would you be able to compare the category theoretical model of the two sentences to discover they had almost the same meaning? You would need some sort of rules that collapse the phrase “person fighting the fire” into a single noun in your noun space, or expand firefighter into a subject, object, and predicate in your phrase space. Similarly you would need to know how to map passive verbs and active verbs into the same space. If the noun space, by itself, is rich enough to represent the meaning of a word like “wedding” which means, roughly, “event where a couple marries” then why wouldn’t it be able to represent a word that means “event where a firefighter rescues a cat”?

Posted by: Doug Summers-Stay on February 9, 2018 2:33 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

The initial main point of our approach was exactly to address this issue. All previous approaches had different spaces for different sentence structures. We collapse all sentences in the unique sentence space and then can use, in the case of vector spaces, that inner product to compare meanings. These are the sort of things that we have subjected to experimental validation. To get non-trivial examples, the use of Frobenius algebra structure for relative pronouns has been crucial:

Sadrzadeh, Clark & Coecke, The Frobenius anatomy of word meanings I: subject and object relative pronouns (https://arxiv.org/abs/1404.5278).

Posted by: bob on February 10, 2018 12:14 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thank you, this paper makes it much clearer to me how this approach would work in practice.

Posted by: Doug Summers-Stay on February 12, 2018 9:48 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Hi all, I am addressing some issues asked by Cory and Jade in the original posting.

1) Language is packed with ambiguity as well on the level of grammar as on the level of meaning. E.g. queen could be a rock band, a chess piece, a bee, a funny-coloured blood person or a drag q. A big problem of NLP is dealing with these ambiguities, which need to be resolved by means of context. We have done some work on that resolving noun ambiguities, using density matrices to represent them:

Piedeleu, Kartsaklis, Coecke & Sadrzadeh. Open System Categorical Quantum Semantics in Natural Language Processing (arXiv:1502.00831).

Now, to address ambiguity in grammar one possibly could do something similar, but one then needs a context of a wider piece of text to disambiguate. An other solution would be to make grammar and meaning less separate, like is obviously the case in machine learning.

2) Dealing with dimensionality has one obvious and equally non obvious solution:

Zeng & Coecke, Quantum Algorithms for Compositional Natural Language Processing (arXiv:1608.01406).

back to the present reality, one could also use “hypothesised” internal structure of verbs to do so e.g.:

Kartsaklis, Sadrzadeh, Pulman & Coecke, Reasoning about Meaning in Natural Language with Compact Closed Categories and Frobenius Algebras (arXiv:1401.5980).

In practice, there are a lot of standard techniques to make matrices more sparse.

3) What is a sentence space? This could be task driven, for example of one wants to do a classification task, e.g. classy newspaper articles, that it would be spanned by the categories of classification. One may however want them to be closer to what sentences mean to humans. Something like that was attempted in Interacting Conceptual spaces I (arXiv:1703.08314), but I would love to see a model where the sentence spaces are movies. We are working on that now, following ideas of Peter Gardenfors.

4) Our approach is put in the context of previous work, in the paper:

Clark & Pulman, Combining Symbolic and Distributional Models of Meaning, AAAI, 2008.

Which started from the Smolensky & Legendre setting (and resulted in the Smolensky and Pulman confusion), and mentions the problems of doing so. Main problem is that the sentence tensor space grows with adding words, and that also the grammatical structure ads to the size of the tensor space. This has the following additional problem: the sentence space depends on grammatical structure. The regroup (or whatever grammar) reductions cut the huge tensor space down to a unique one. The Pet Fish thing has been addresses within our setting here:

Coecke & Lewis, A Compositional Explanation of the Pet Fish Phenomenon (arXiv:1509.06594).

5) Empirical validating of the model includes the papers:

At the time these outperformed existing methods but meanwhile Machine Learning has taken over.

Posted by: bob on February 10, 2018 10:20 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Hi, thank you for your response to our questions; you’ve given me a lot to think about.

We have done some work on that resolving noun ambiguities, using density matrices to represent them

This is a really cool way to solve that problem.

Now, to address ambiguity in grammar one possibly could do something similar, but one then needs a context of a wider piece of text to disambiguate. An other solution would be to make grammar and meaning less separate, like is obviously the case in machine learning.

As I understand it, there are two types of grammar ambiguity; not always having a unique type reduction and not having a unique way to assign words to their grammatical type. For the first ambiguity you suggest using a grammar category which somehow allows for the “superposition” of two type reductions. My idea for the second ambiguity is to make the quantization functor more specific by “populating it” with a set of words. Built into the functor should be a assignment of specific words to their grammatical roles and place in the vector space (or a different semantics category). Then, when you want a word to have a different grammatical or distributional meaning, you make a new functor where that is true. We could also define a suitable form of morphism between these functors allowing you update and change the choices that you made.

In Zeng & Coecke, Quantum Algorithms for Compositional Natural Language Processing (arXiv:1608.01406) you extend the pregroup DisCoCat model to a functor. How do you reconcile the issue that Preller found? Is this fixed by using Frobenius algebras?

but I would love to see a model where the sentence spaces are movies.

Do you mean a vector space representing for example the RGB values of images? This sounds very interesting.

I don’t have any comments on the rest of what you said yet. However, I am excited to read through these papers and learn about the various ways to answer our questions.

Posted by: Jade Master on February 10, 2018 10:06 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Hi Jade,

The functor things is a bit of clumsiness, since while mathematically wrong, it is morally right :) I used to use a product of categories to combine the two (which of course has no technical issues), but people seem to like more the idea of imposing grammar on meaning. A thing about a regroup is that it has more structure than you actually use, since you only ned the reductions, and this also takes away the technical problem.

Concerning the movies, I really mean movies as we imagine them in our minds. Probably the easiest way to go about this is to take 3+1D space and fill it in with characters. Prepositions will then play a key role in relative placings.

Posted by: bob on February 12, 2018 2:17 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

There’s been more discussion of this blog article over on Google+, which I’ll copy here.

I wrote:

Now students in the Applied Category Theory class are reading about categories applied to linguistics. Read the blog article here for more.

This was written by my grad student Jade Master along with Cory Griffith, an undergrad at Stanford.

What’s the basic idea? I don’t know much about this, but I can say a bit.

Since category theory is great for understanding the semantics of programming languages, it makes sense to try it for human languages, even though they’re much harder. The first serious attempt I know was by Jim Lambek, who introduced pregroup grammars in 1958:

• Joachim Lambek, The mathematics of sentence structure, Amer. Math. Monthly 65 (1958), 154–170.

In this article he hid the connection to category theory. But when you start diagramming sentences or phrases using his grammar, as below, you get planar string diagrams. So it’s not surprising - if you’re in the know - that he’s secretly using monoidal categories where every object has a right dual and, separately, a left dual.

This fact is just barely mentioned in the Wikipedia article:

• Pregroup grammar.

but it’s explained in more detail here:

• A. Preller and J. Lambek, Free compact 2-categories, Mathematical Structures in Computer Science 17 (2005), 309-340.

This stuff is hugely fun, so I’m wondering why I never looked into it before! When I talked to Lambek, who is sadly no longer with us, it was mainly about his theories relating particle physics to quaternions.

Recently Mehrnoosh Sadrzadeh and Bob Coecke have taken up Lambek’s ideas, relating them to the category of finite-dimensional vector spaces. Choosing a monoidal functor from a pregroup grammar to this category allows one to study linguistics using linear algebra! This simplifies things, perhaps a bit too much - but it makes it easy to do massive computations, which is very popular in this age of “big data” and machine learning.

It also sets up a weird analogy between linguistics and quantum mechanics, which I’m a bit suspicious of. While the category of finite-dimensional vector spaces with its usual tensor product is monoidal, and has duals, it’s symmetric, so the difference between writing a word to the left of another and writing it to the right of another gets washed out! I think instead of using vector spaces one should use modules of some noncommutative Hopf algebra, or something like that. Hmm… I should talk to those folks.

Noam Zeilberger wrote:

You might have been simplifying things for the post, but a small comment anyways: what Lambek introduced in his original paper are these days usually called “Lambek grammars”, and not exactly the same thing as what Lambek later introduced as “pregroup grammars”. Lambek grammars actually correspond to monoidal biclosed categories in disguise (i.e., based on left/right division rather than left/right duals), and may also be considered without a unit (as in his original paper). (I only have a passing familiarity with this stuff, though, and am not very clear on the difference in linguistic expressivity between grammars based on division vs grammars based on duals.)

Noam Zeilberger wrote:

If you haven’t seen it before, you might also like Lambek’s followup paper “On the calculus of syntactic types”, which generalized his original calculus by dropping associativity (so that sentences are viewed as trees rather than strings). Here are the first few paragraphs from the introduction:

…and here is a bit near the end of the 1961 paper, where he made explicit how derivations in the (original) associative calculus can be interpreted as morphisms of a monoidal biclosed category:

John Baez wrote:

Noam Zeilberger wrote: “what Lambek introduced in his original paper are these days usually called “Lambek grammars”, and not exactly the same thing as what Lambek later introduced as “pregroup grammars”.”

Can you say what the difference is? I wasn’t simplifying things on purpose; I just don’t know this stuff. I think monoidal biclosed categories are great, and if someone wants to demand that the left or right duals be inverses, or that the category be a poset, I can live with that too…. though if I ever learned more linguistics, I might ask why those additional assumptions are reasonable. (Right now I have no idea how reasonable the whole approach is to begin with!)

Thanks for the links! I will read them in my enormous amounts of spare time. :-)

Noam Zeilberger wrote:

As I said it’s not clear to me what the linguistic motivations are, but the way I understand the difference between the original “Lambek” grammars and (later introduced by Lambek) pregroup grammars is that it is precisely analogous to the difference between a monoidal category with left/right residuals and a monoidal category with left/right duals. Lambek’s 1958 paper was building off the idea of “categorial grammar” introduced earlier by Ajdukiewicz and Bar-Hillel, where the basic way of combining types was left division A\B and right division B/A (with no product).

Noam Zeilberger wrote:

At least one seeming advantage of the original approach (without duals) is that it permits interpretations of the “semantics” of sentences/derivations in cartesian closed categories. So it’s in harmony with the approach of “Montague semantics” (mentioned by Richard Williamson over at the n-Cafe) where the meanings of natural language expressions are interpreted using lambda calculus. What I understand is that this is one of the reasons Lambek grammar started to become more popular in the 80s, following a paper by Van Benthem where he observed that such such lambda terms denoting the meanings of expressions could be computed via “homomorphism” from syntactic derivations in Lambek grammar.

Jason Nichols wrote:

John Baez, as someone with a minimal understanding of set theory, lambda calculus, and information theory, what would you recommend as background reading to try to understand this stuff?

It’s really interesting, and looks relevant to work I do with NLP and even abstract syntax trees, but I reading the papers and wiki pages, I feel like there’s a pretty big gap to cross between where I am, and where I’d need to be to begin to understand this stuff.

John Baez wrote:

Jason Nichols - I suggest trying to read some of Lambek’s early papers, like this one:

• Joachim Lambek, The mathematics of sentence structure, Amer. Math. Monthly 65 (1958), 154–170.

(If you have access to the version at the American Mathematical Monthly, it’s better typeset than this free version.) I don’t think you need to understand category theory to follow them, at least not this first one. At least for starters, knowing category theory mainly makes it clear that the structures he’s trying to use are not arbitrary, but “mathematically natural”. I guess that as the subject develops further, people take more advantage of the category theory and it becomes more important to know it. But anyway, I recommend Lambek’s papers!

Borislav Iordanov wrote:

Lambek was an amazing teacher, I was lucky to have him in my ungrad. There is a small and very approachable book on his pregroups treatment that he wrote shortly before he passed away: “From Word to Sentence: a computational algebraic approach to grammar”. It’s plain algebra and very fun. Sadly looks like out of print on Amazon, but if you can find it, well worth it.

Andreas Geisler wrote:

One immediate concern for me here is that this seems (don’t have the expertise to be sure) to repeat a very old mistake of linguistics, long abandoned :

Words do not have atomic meanings. They are not a part of some 1:1 lookup table.

The most likely scenario right now is that our brains store meaning as a continuously accumulating set of connections that ultimately are impacted by every instance of a form we’ve ever heard/seen.

So, you shall know a word by all the company you’ve ever seen it in.

Andreas Geisler wrote:

John Baez I am a linguist by training, you’re welcome to borrow my brain if you want. You just have to figure out the words to use to get my brain to index what you need, as I don’t know the category theory stuff at all.

It’s a question of interpretation. I am also a translator, so i might be of some small assistance there as well, but it’s not going to be easy either way I am afraid.

John Baez wrote:

Andreas Geisler wrote: “I might be of some small assistance there as well, but it’s not going to be easy either way I am afraid.”

No, it wouldn’t. Alas, I don’t really have time to tackle linguistics myself. Mehrnoosh Sadrzadeh is seriously working on category theory and linguistics. She’s one of the people leading a team of students at this Applied Category Theory 2018 school. She’s the one who assigned this paper by Lambek, which 2 students blogged about. So she would be the one to talk to.

So, you shall know a word by all the company you’ve ever seen it in.

Yes, that quote appears in the blog article by the students, which my post here was merely an advertisement for.

Posted by: John Baez on February 11, 2018 12:00 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

I commented to John on Google+, and post it here too for the sake of having things in one place.

John, you’re perfectly right to have problems with picking vector spaces for meaning, which in fact, aren’t even vector spaces but rather spaces of probability distributions, where sums don’t mean much. There are three issues here, the connection with quantum theory, the use of vector spaces, their symmetry as opposed to the non-commutativity of language. I start with the latter.

I also used to think that the meaning category should at least reflect the grammatical structure, and so in particular, the non-commutativity of language. Specialists like Moortgat have been insisting about this to us many times. I am however not that sure anymore about the this. The question here is whether the non-commutativity of language has a fundamental ontological status, or whether it is needed for bureaucratic purposes. Here is my case for the latter. Obviously it is not the case that you can swap words around and retain the meaning (or meaningfulness) of a sentence. That said however, the word-order with respect to grammatical roles is very different for different languages, e.g. for a simple sentence with object, subject and transitive verb, if one spans all languages, all permutations are possible. This seems to indicate the there can’t be a fundamental ontological status of word order. What is fundamental for me is the “wiring”, namely, that object and subject are fed into the transitive verb (cf. our pictures). This is what I now conceive grammar to be, a wiring of words in a sentence. If one represents the sentence in the plain, there is normal reason to retain the word order, as long as the wiring doesn’t change; in fact, there is not even a notion of word order. Of course we can’t speak two-dimensionally, and hence we can’t express this wiring when we speak, and that’s where word-order comes in. It tries to retain something of the wiring, but the manner in which this order is imposed is purely conventional, depending on the language.

Vector spaces are extremely bad at representing meanings in a fundamental way, for example, lexical entailment, like tiger < big cat < mammal < animal can’t be represented in a vector space. At Oxford we are now mainly playing around with alternative models of meaning drawn from cognitive science, psychology and neuroscience. Our:

Interacting Conceptual Spaces I

is an example of this, where we work with convex spaces that are still useful for empirical purposes, following Peter Gardenfors. The manner he writes about how humans think feels to me closely related to the wiring idea. In other papers we have used density matrices both to represent logical entailment and ambiguity in language. But any more models, including non-symmetric ones would be very useful.

Concerning the connection with quantum theory, what we did in our 1st paper is indeed a “grammatical quantum filed theory” i.e. a functor from grammar into vector spaces. Personally, I don’t think anymore (I used to!) that compact closure is that typical for quantum theory. It is a fundamental structure of interaction wherever the whole is not the sum of the parts, which we see al lot. In a way, while Cartesian means “no interaction”, compact closure means “maximal interaction”. A silly paper outlining this idea is:

From quantum foundations via natural language meaning to a theory of everything

and we started to give some formal substance to it in a soon to be publicised paper: Uniqueness of composition in quantum theory and linguistics. The fact that one can get so much of quantum theory out of it is that we have been looking much to long at the world with Cartesian glasses, and when not doing that anymore, quantum theory is not that weird after all.

Back to language, I don’t think that this wiring structure is specific to natural language, nor something even related to humans only. In the context of a hunt lion is perfectly aware of who the pray and who the predator is, and why one is chasing the other, which is exactly what the wiring-structure of a transitive verb sentence tells us. Chomsky used to say that grammar was hard-wired in our brains. I think that instead wires-structure is hard-wired in the world we live in.

Anyway, this is my naive take on the mathematics of language, obviously a view from an outsider who happened to accidentally stumble upon this area.

Posted by: bob on February 12, 2018 10:54 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Okay, so I’ll copy my reply here:

I was just thinking that if you wanted some of the simplifying benefits of linear algebra but also wanted to avoid the symmetric monoidal structure built into the category of finite-dimensional vector spaces, there are some fun things you could try. Lambek seems to like monoidal categories where every object has a right and a left dual. One example is the category of representations of a non-cocommutative Hopf algebra. There are lots of these, and some have categories of representations that are pretty easy to compute with. So, you could try generalizing vector space models of meaning to models that use such categories.

I’m mainly interested in this idea because it’s mathematically cute. “Quasitriangular” Hopf algebras, like the famous “quantum groups”, have categories of representations that are braided monoidal, with all objects having duals. These are famous for their applications to physics where there are 2 dimensions of space and 1 dimension of time - like thin films of condensed matter. Everyone and his brother is studying these thanks to their possible applications to topological quantum computation. But Hopf algebras whose categories of representations are just monoidal with duals, not braided, should be important in physics where there’s 1 dimension of space and 1 of time—where you can’t switch things around. These seem to be less popular. So it would be very cute if they showed up when studying grammar, which has a famous linear aspect to it.

Posted by: John Baez on February 12, 2018 6:13 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

If you take the “many nouns can also be used as adjectives” too seriously, could you use that to get a K-V 2-Vect by putting all the possibilities in? I’m imagining there are a fixed number of grammatical types. Then do some Tannakian nonsense?

Posted by: Ammar Husain on February 18, 2018 8:51 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

See my ultimate ‘model of model of models’ here:

The Model of Model of Models

Links to 27 wiki-books, including the ones I mentioned above

(links weren’t formatted properly in my earlier post, so I’m giving the links to the named wiki-books again here)

Linguistics Crash Course

Mathematical Logic Crash Course

Computational Logic Crash Course

Posted by: zarzuelazen on February 12, 2018 3:21 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Oddly, I have been using Category Theory as a tool for doing linguistic semantics for quite a while, from before it became a thing, in fact, drawing on Saunders MacLane and before that the Bourbakists (I started with MacLane and Birkhoff’s Algebra), and I’ve found it very useful, but I take quite a different approach from the one most people seem to be taking, since I use the formal concepts descriptively (in describing objectlanguage meaning, both individual acts of meaning and the categorial structures (including combinatorial schemata) that make them possible.) I call what I do “descriptive linguistic semantics”, and I’m concerned with understanding the possibilities for expressing meaning in the world’s natural language systems, so I’m concerned with the various ways language “hooks on to the world”, to use Putnam’s phrase, and thus with the quintessential fact about natural language, and that is the relation of reference, which I regard as a relation between the meaning of a linguistic expression and an intentional object “in the world”, a relation which I’m not sure exists in language use in the formal mode. For this reason, I don’t think doing semantics in the formal mode, as with Tarskian, formal or model-theoretic semantics is a promising way to go. My approach is similar to the way physicists use mathematical concepts to describe reality, but my object would include not only the world, but the concepts physicists use to describe the world. (My inclinations are rather Kantian.) I wanted to suggest, for example, that if we want to understand how mathematical thinking works, we need not another formal language structure on essentially the same logical level, but a language that can refer to the meanings of mathematical expressions and to the categories of the working mathematician as distinct from the “inscriptions” that index them, which are used intuitively in the formal mode. It’s an ongoing project, and I hope the results of my struggles will begin to appear soon, but I just wanted to indicate that there are possibilities for the applications of Category Theory in linguistic semantics other than or in addition to AI, NLP or formal semantics.

Posted by: James Dennis on February 14, 2018 12:44 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

[I missed this was its own blog post and also posted on the google+ topic.]

There’s also a very close connection to linear logic and type theory through the Curry-Howard morphism. A lot of people work on these theories under the heading “categorial grammar” or “type-logical grammar”. An example is my book on type-logical semantics and Glyn Morrill’s book on type-logical grammar. Michael Moortgat and his students also wrote on this extensively. I think Michael and Dick Oehrle were working on a book, too—they were teaching the foundations at all the linguistic and logic summer schools.

The sentence diagrams in the post are closely connected to proof net diagrams in type-logical grammars. Glyn and I make that connection in a joint paper on parsing.

This isn’t competing with or less formal than Montague’s grammar. The sequent formulation of Lambek’s calculus completes Montague’s approach to quantifier scope. Montague only had binding (quantifying-in), but not a proper theory of abstraction. Lambek’s calculs and type-logical grammar solves all this. The sequent quantifying-in rule looks just like Montague’s quanitfying-in rule. Now this isn’t quite straight Lambek—you need to go off and do some non-local binding.

I haven’t worked on this stuff in ages, so I’m curious as to where the field’s gone. The activity when I left was largely around bounding long-distance dependencies in a natural way (limited associativity), primarily with modal constructs. That, and sentential binding operations like quantifier scoping, as well as word order in languages less strict than English.

P.S. Speaking of coincidences, I was referred by a physicist to Baez and Munian’s book on gauge theory for its intro to smooth manifolds, which was just what I needed to understand some of the Hamiltonian Monte Carlo sampling algorithms we’re using for Stan.

Posted by: Bob Carpenter on February 18, 2018 9:39 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

[I missed this was its own blog post and also posted on the google+ topic.]

The sentence diagrams in the post are closely connected to proof net diagrams in type-logical grammars. Glyn and I make that connection in a joint paper on parsing.

Posted by: Bob Carpenter on February 18, 2018 9:40 PM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Adding to Bob Carpenter’s comment, there is also an approach to the syntax-semantics interface called ‘glue semantics’, which is directly based on implicational linear logic with tensors, so that the ‘no copying, no deletion’ maxim plays a direct role in the proceedings, rather than following from other provisions, as is often the case.

Various kinds of systems are used, but it can be done with bare propositional linear logic aka smccs.

Posted by: Avery Andrews on February 20, 2018 1:33 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

It seems I’m a bit late to the party! I came across this blog post while googling about the correlation between category theory and pregroup grammar, as I have been puzzled by a specific question about Lambek’s theory.

My question is: What are Lambek’s left/right adjoints in categorical terms? Aren’t adjoints supposed to be functors? What does it mean to say an object $p\in P$ has both a left adjoint $p^l$ and a right adjoint $p^r$ ?

I guess I might be missing some background assumption here (e.g., about the source and target categories of the adjoint functors) but I haven’t seen this piece of terminology satisfactorily clarified in any of Lambek’s original writings that I have managed to find. He keeps saying that the adjoint terminology is borrowed from category theory but doesn’t specify how the pregroup adjoints correspond to categorical adjoints…

Any explanation or reference would be appreciated!

Posted by: Julio Song on July 11, 2020 4:24 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Julio wrote:

Aren’t adjoints supposed to be functors?

That’s one example of the general concept of ‘adjoint’, but we can talk about morphisms in any 2-category being adjoints. If this 2-category is $\mathsf{Cat}$ , these are adjoint functors. If it’s the 2-category $\mathsf{BA}$ corresponding to a monoidal category $\mathsf{A}$ , then the morphisms in $\mathsf{BA}$ are objects of $\mathsf{A}$ , and that’s the case we’re using here. In this case the adjoints are often called ‘duals’—click the link for more on all this.

Posted by: John Baez on July 12, 2020 12:14 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thank you very much for your prompt answer, John! I’m learning a lot from your patient explanation (as always). I have met the concept “dual” before but never realized that it was another name for adjoints. I’ll catch up on my learning of category theory and (hopefully) enter the world of 2-categories soon.

Posted by: Julio Song on July 12, 2020 8:16 AM | Permalink | Reply to this

Re: Linguistics Using Category Theory

$MathML-enabled post (click for more details).$

Thanks! For now, if you get the idea of ‘left duals’ and ‘right duals’ of objects in a monoidal category, then you can relax in the knowledge that ‘left adjoints’ and ‘right adjoints’ of objects in a monoidal category are the same as those.

Posted by: John Baez on July 12, 2020 6:47 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

February 6, 2018