The n-Category Café

The idea here is we may want to take something like a graph with edges labelled by positive numbers:

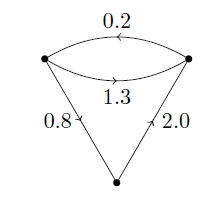
and say that some of its nodes are ‘inputs’, while others are ‘outputs’:

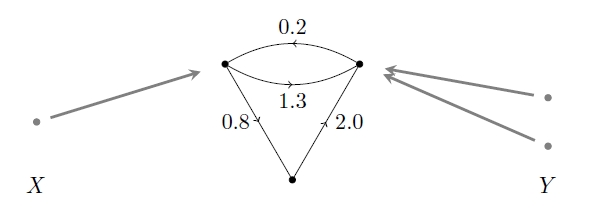
This lets us treat our labelled graph as a ‘morphism’ from the set $X$ to the set $Y$.

The point is that we can compose such morphisms. For example, suppose we have another one of these things, going from $Y$ to $Z$:

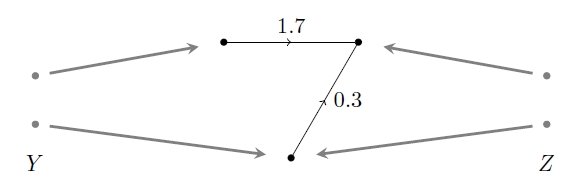
Since the points of $Y$ are sitting in both things:

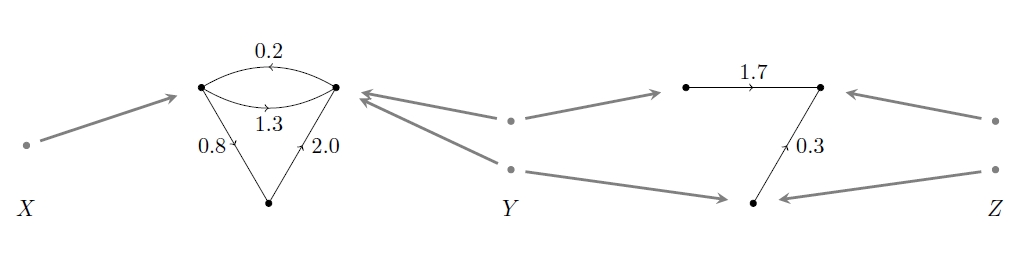
we can glue them together and get a thing going from $X$ to $Z$:

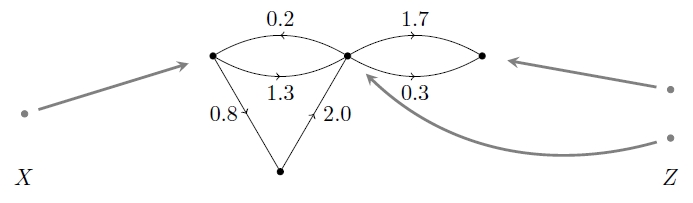
That’s how we compose these morphisms.

Note how we’re specifying some nodes of our original thing as inputs and outputs:

We’re using maps from two sets $X$ and $Y$ to the set $N$ of nodes of our graph. And a bit surprisingly, we’re not demanding that these maps be one-to-one. That turns out to be useful—and in general, when doing math, it’s dumb to make your definitions forbid certain possibilities unless you really need to.

So, our thing is really a cospan of finite sets—that is, a diagram of finite sets and functions like this:

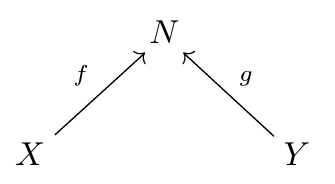
together some extra structure on the set $N$. This extra structure is what Brendan calls a decoration, and it makes the cospan into a ‘decorated cospan’. In this particular example, a decoration on $N$ is a way of making it into the nodes of a graph with edges labelled by positive numbers. But one could consider many other kinds of decorations: this idea is very general.

To formalize the idea of ‘a kind of decoration’, Brendan uses a functor

$$F: {FinSet} \to {Set}$$

sending each finite set $N$ to a set of $F(N)$. This set $F(N)$ is the set of decorations of the given kind that we can put on $N$.

So, for any such functor $F$, a decorated cospan of finite sets is a cospan of finite sets:

together with an element of $F(N)$.

But in fact, Brendan goes further. He’s not content to use a functor

$F: {FinSet} \to {Set}$

to decorate his cospans.

First, there’s no need to limit ourselves to cospans of finite sets: we can replace ${FinSet}$ with some other category! If $C$ is any category with finite colimits, there’s a category ${Cospan}(C)$ with:

• objects of $C$ as its objects,
• isomorphism classes of cospans between these as morphisms.

Second, there’s no need to limit ourselves to decorations that are elements of a set: we can replace ${Set}$ with some other category! If $D$ is any symmetric monoidal category, we can define an element of an object $d \in D$ to be a morphism

$f: I \to d$

where $I$ is the unit for the tensor product in $D$.

So, Brendan defines decorated cospans at this high level of generality, and shows that under some mild conditions we can compose them, just as in the pictures we saw earlier.

Here’s one of the theorems Brendan proves:

Theorem. Suppose $C$ is a category with finite colimits, and make $C$ into a symmetric monoidal category with its coproduct as the tensor product. Suppose $D$ is a symmetric monoidal category, and suppose $F: C \to D$ is a lax symmetric monoidal functor. Define an F-decorated cospan to be a cospan

in $C$ together with an element of $F(N)$. Then there is a category with

• objects of $C$ as its objects,
• isomorphism classes of $F$-decorated cospans as its morphisms.

This is called the F-decorated cospan category, $FCospan$. This category becomes symmetric monoidal in a natural way. It is then a dagger compact category.

(You may not know all this jargon, but ‘lax symmetric monoidal’, for example, talks about how we can take decorations on two things and get a decoration on their disjoint union, or ‘coproduct’. We need to be able to do this—as should be obvious from the pictures I drew. Also, a ‘dagger compact category’ is the kind of category whose morphisms can be drawn as networks.)

Brendan also explains how to get functors between decorated cospan categories. We need this in our paper on electrical circuits, because we consider several categories where morphisms is a circuit, or something that captures some aspect of a circuit. Most of these categories are decorated cospan categories. We want to get functors between them. And often we can just use Brendan’s general results to get the job done! No fuss, no muss: all the hard work has been done ahead of time.

I expect to use this technology a lot in my work on network theory. You’ll see another application in my next post here!